§ 6.2. Монохроматичні світлові хвилі

У відповідності з електромагнітною теорією (розділ 5) плоска світлова хвиля, що поширюється вздовж напрямку r, описується системою рівнянь для електричної та магнітної складових хвилі:

, (6.11)

де – відповідні амплітуди,  – циклічна частота хвилі, – хвильове число ( – довжина хвилі), ₀ – початкова фаза.

В більшості оптичних явищ дія світла на речовину визначається електричним вектором електромагнітного поля. Світлове випромінювання (  10¹⁵ Гц) не призводить до намагнічування середовища. Тому, саме вектор називають світловим вектором, а перше рівняння системи (6.11) називають рівнянням плоскої світлової хвилі.

Світлова хвиля називається монохроматичною, якщо амплітуда , частота , а початок і кінець хвилі жодним чином не обмежені, тобто . Однак, оскільки тривалість процесу випромінювання електромагнітних хвиль окремими атомами є скінченною , то світло є сукупністю просторово обмежених хвиль (цугів). В подальшому, як правило, будемо оперувати поняттям монохроматичних світлових хвиль.

Якщо дві монохроматичні хвилі однакової частоти накладаються в певній точці простору, то їх різниця фаз

за рахунок випадковості і непередбачуваності початкових фаз не буде залишатись постійною в часі. Якщо ж обидві хвилі мають спільне походження , то . Хвилі однакової частоти, що мають постійну в часі різницю фаз, називають когерентними. Якщо врахувати, що хвильове число

,

де n – показник заломлення середовища, в якому поширюється хвиля, а ₀ – довжина світлової хвилі у вакуумі, то

.

Тут  – оптична різниця ходу когерентних світлових хвиль (променів), оскільки добуток називається оптичним шляхом променя. Зрозуміло, що для когерентних світлових хвиль оптична різниця ходу не залежить від часу.

§ 6.3. Інтерференція світла

І

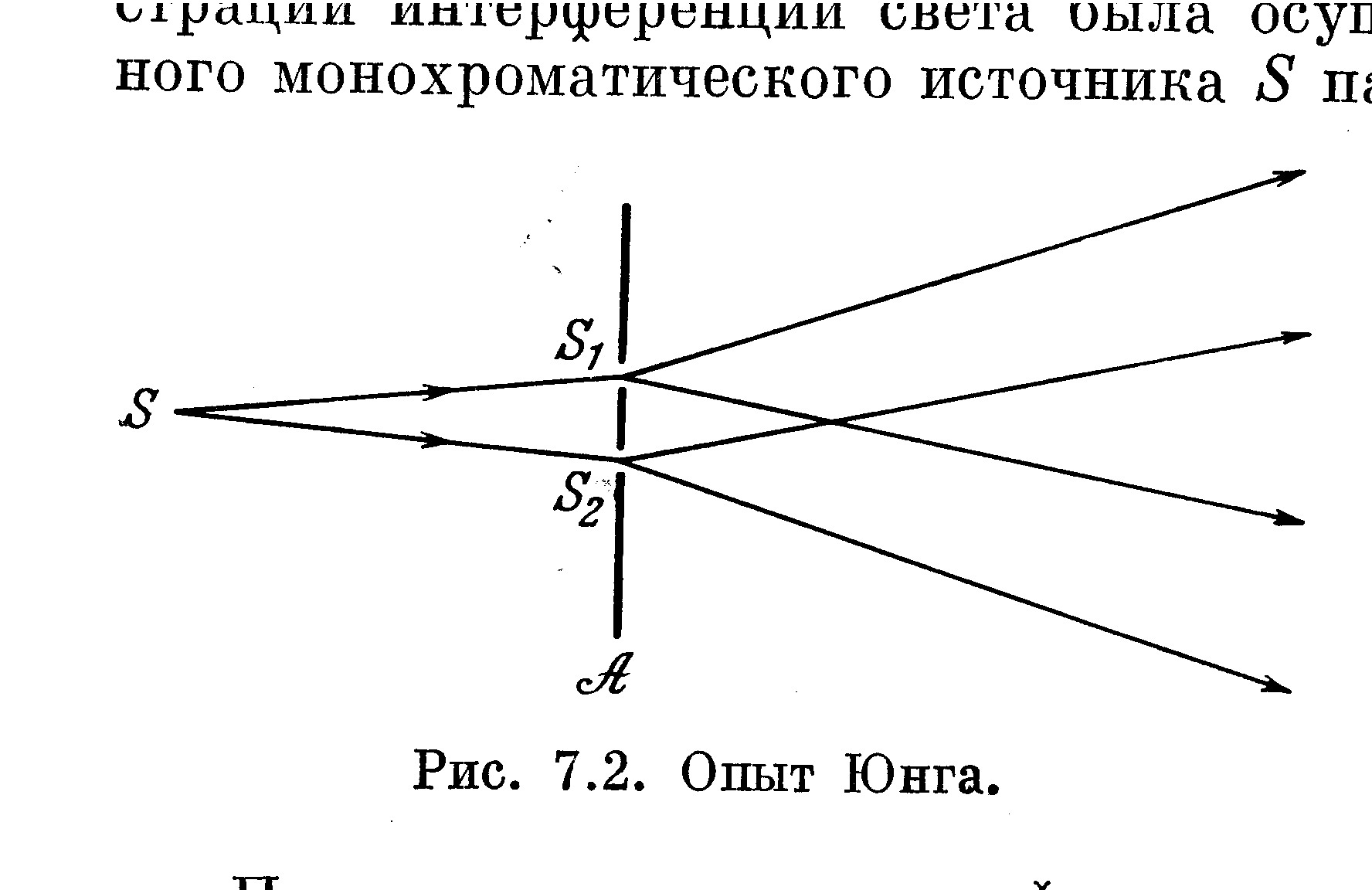Рис. 6.5

нтерференція світла – це явище накладання когерентних світлових хвиль, в результаті якого відбувається перерозподіл світлової енергії в просторі. В точках простору, куди когерентні хвилі приходять у фазі, вони підсилюють одна одну; в точках, куди вони попадають у протифазі, відбувається послаблення світла. На екрані спостерігається характерна інтерференційна картина у вигляді чергування темних і світлих смуг – максимумів і мінімумів освітленості, якщо падаюче світло монохроматичне. Відмітимо, що сказане має місце лише тоді, коли напрямки коливань світлового вектора обох хвиль співпадають.

У випадку максимуму інтенсивності інтерференційної картини в оптичній різниці ходу двох когерентних хвиль вкладається ціле число довжин хвиль (у вакуумі) , тобто

. (6.12)

Мінімум інтерференції спостерігається, коли в оптичній різниці ходу вкладається непарне число півхвиль, тобто

. (6.13)

Когерентні хвилі отримують двома способами: поділом фронту хвилі та поділом амплітуди хвилі. До поділу фронту хвилі можна віднести такі схеми утворення когерентних хвиль: дослід Юнга, дзеркала Френеля, біпризма Френеля.

У

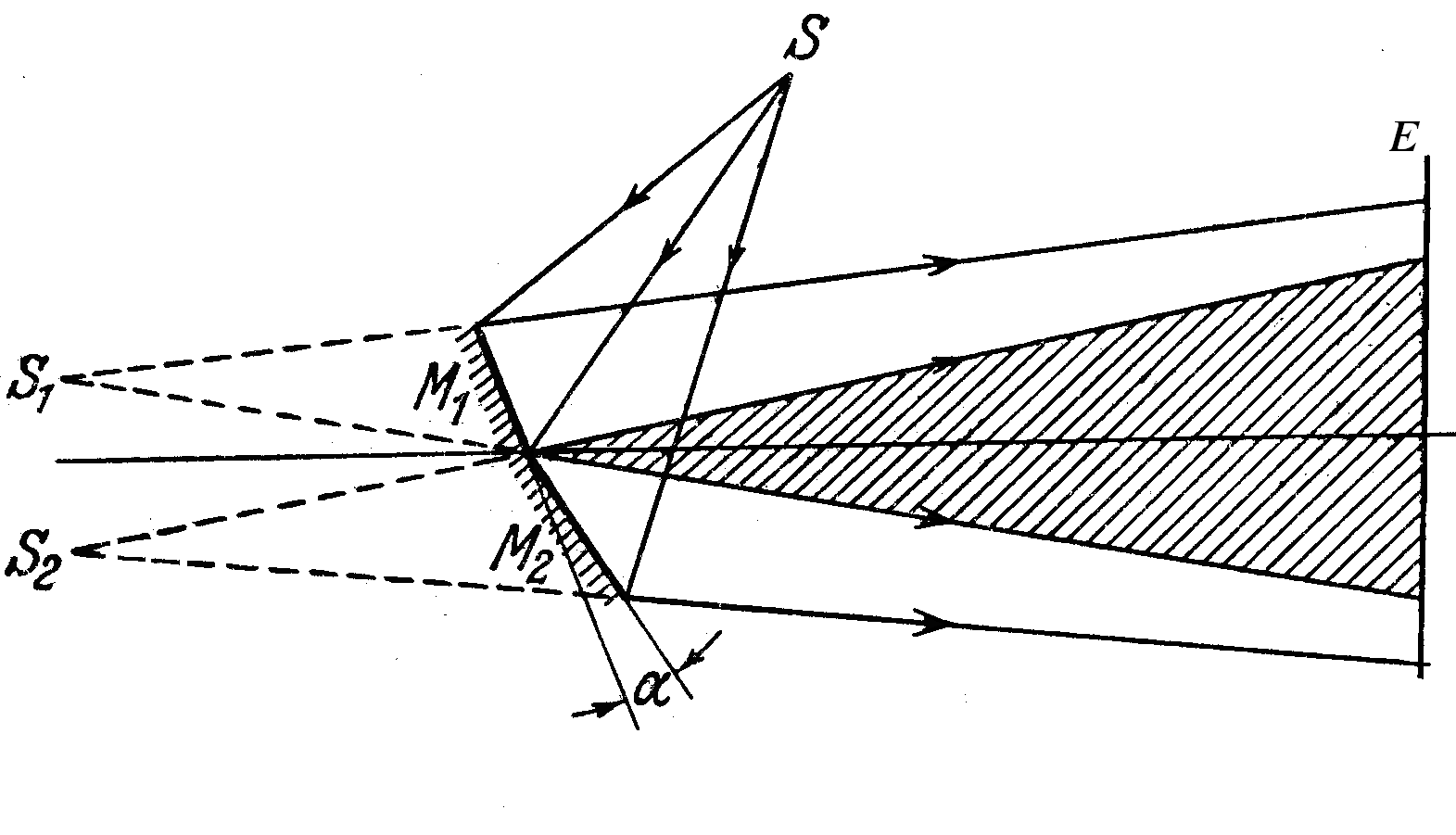Рис. 6.6

досліді Юнга світло від точкового монохроматичного джерела S падає на два невеликих отвори та в екрані А, розміщені на рівних відстанях від джерела S (рис. 6.5). Ці отвори діють як вторинні монохроматичні точкові синфазні джерела. Поділений таким чином фронт хвилі дозволяє спостерігати інтерференційну картину в області перекриття світлових пучків від джерел та .

У методі дзеркал Френеля використовують два плоскі дзеркала М₁ і М₂ (рис. 6.6), кут  між якими дуже малий. Світло від точкового джерела S, внаслідок відбивання від обох дзеркал утворює два уявних зображення і , які діють як когерентні джерела. Хвилі від цих джерел накладаються і дають на екрані Е інтерференційну картину.

В

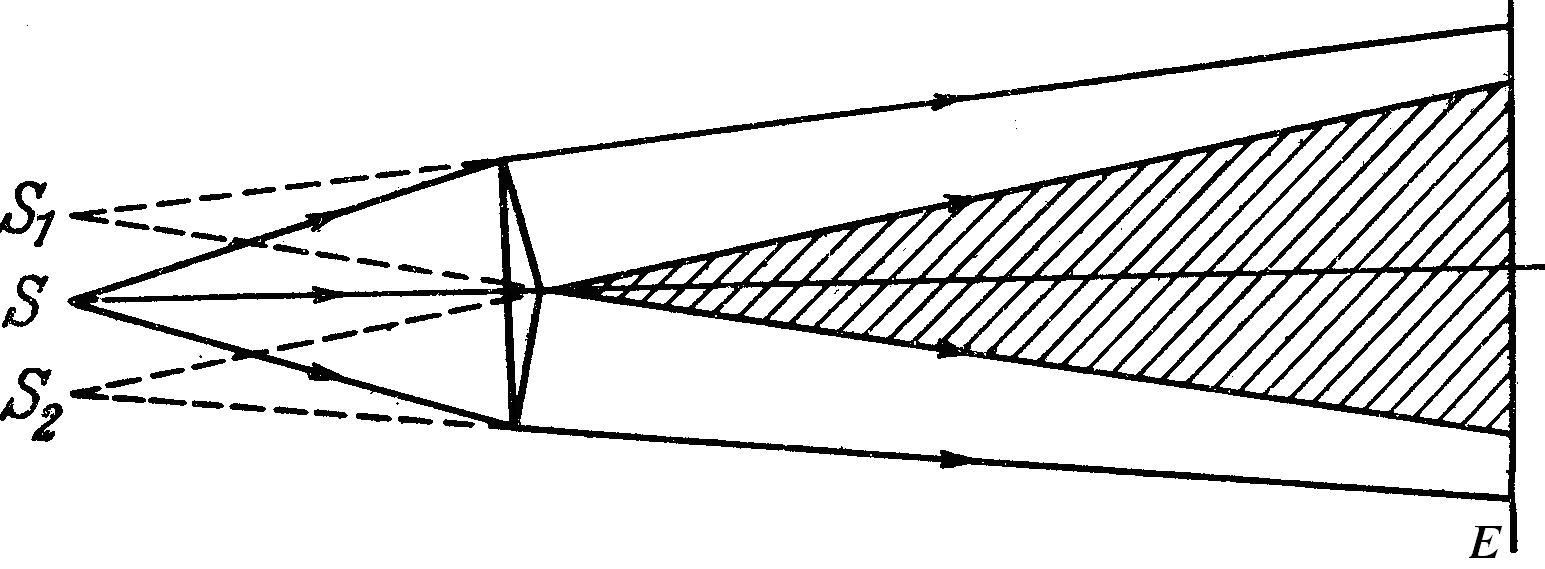Рис. 6.7

іншому методі спостереження інтерференції використовують біпризму Френеля, яка складається з двох однакових скляних призм з невеликим заломлюючим кутом (рис. 6.7). Світло від джерела S заломлюючись в призмі, ділиться на дві хвилі, які відповідають когерентним уявним джерелам і . Розрахунок інтерференційної картини на екрані, яку дістають за допомогою біпризми Френеля або дзеркал Френеля, нічим не відрізняється від приведеного нижче розрахунку для досліду Юнга.

Р

Рис. 6.8

озглянемо дві когерентні світлові хвилі, що йдуть від джерел S₁ i S₂; d – відстань між джерелами (рис. 6.8). На екрані Е внаслідок інтерференції спостерігається інтерференційна картина у вигляді світлих і темних смуг. Обчислимо ширину цих смуг припускаючи, що пряма S₁S₂ паралельна до площини екрану. Позначимо координати інтерференційного максимуму чи мінімуму як х_m. З трикутника S₂PD₂ маємо

,

а з трикутника S₁PD₁ –

.

Звідси і тому . З умов і випливає, що Отже, координата пов’язана з оптичною різницею ходу  співвідношенням

. (6.14)

З врахуванням умов (6.12, 6.13), отримаємо координати максимумів

(6.15)

та мінімумів інтенсивності світла

(6.16)

Відстань між двома сусідніми мінімумами інтенсивності визначає ширину інтерференційної смуги. Згідно з (6.15) і (6.16),

(6.17)

Очевидно, що відстань між інтерференційними максимумами (відстань між смугами) буде така ж сама. З (6.17) видно, що відстань зростає при зменшенні відстані d між джерелами S₁ i S₂. Інтерференційна картина буде чіткою при умові Вимірюючи , можна експериментально визначити довжину світлової хвилі.