§ 5.10. Хвильове рівняння

Хвильове рівняння – це диференціальне рівняння, розв’язком якого є рівняння хвилі. Для встановлення хвильового рівняння співставимо другі частинні похідні по координатах і часу від рівняння хвилі (5.50)

.

Тоді:

, (5.51)

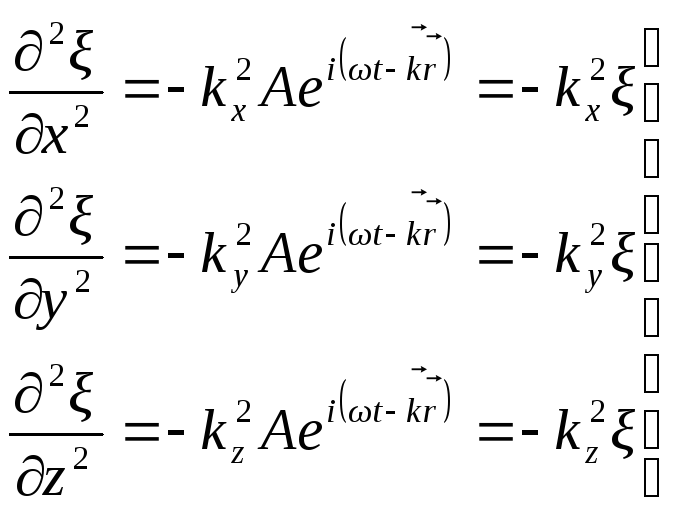(5.52)

Просумуємо систему рівнянь (5.52):

. (5.53)

Співставляючи (5.51) і (5.53), одержимо

. (5.54)

Оскільки

, (5.55)

то остаточно хвильове рівняння набуває вигляду

. (5.56)

Ліву частину цього рівняння можна лаконічно записати, використовуючи оператор Лапласа як суму других частинних похідних по х, у, z від функції цих змінних. Тоді хвильове рівняння матиме вигляд

.

Для плоскої хвилі, що поширюється вздовж осі х, хвильове рівняння набуде вигляду

. (5.57)

Поширення коливань у пружному середовищі зумовлене поширенням деформації середовища під дією джерела хвилі. І тому швидкість поширення хвилі повинна визначатись пружними характеристиками середовища.

Зокрема, швидкість поздовжніх хвиль в твердих тілах

, (5.58)

в рідинах і газах

, (5.59)

де Е – модуль Юнга, k – модуль всебічного стиску.

Швидкість поперечних хвиль в твердих тілах

де G – модуль зсуву.

Швидкість звуку в газах

де – відношення молярних чи питомих теплоємностей при сталих тиску та об’єму, – універсальна газова постійна, Т – термодинамічна температура, μ – молярна маса газу.

§ 5.11. Енергія пружної хвилі

Енергія пружної хвилі складається з кінетичної енергії коливного руху частинок і потенціальної енергії, зумовленої деформацією. Виберемо елементарний циліндр пружного середовища ∆V настільки малим, щоб відносна деформація і швидкість у всіх точках об’єму, відповідно, були однаковими. Тоді потенціальна енергія елементарного деформованого циліндра

. (5.60)

Оскільки у відповідності з (5.58)

,

то

. (5.61)

Кінетична енергія даного об’єму ∆v буде

,

де m = ρ∆v – маса об’єму ∆v.

Повна енергія елемента об’єму хвилі

,

а густина енергії – енергія одиниці об’єму

. (5.62)

Використавши рівняння плоскої хвилі

,

отримаємо

,

.

Підставляючи ці похідні в (5.62), отримаємо для густини енергії

. (5.63)

Із (5.63) видно, що густина енергії w в кожен момент часу у різних точках простору різна. В деякій точці х густина енергії змінюється з часом за законом квадрату синуса. Оскільки усереднене по часу значення квадрату синуса дорівнює , то середнє значення густини енергії в кожній точці буде

.

Потік енергії Ф – це фізична величина, чисельно рівна енергії, яка переноситься хвилею за одиницю часу через деяку поверхню:

.

Під густиною потоку розуміють енергію, яка переноситься хвилею за одиницю часу через одиничну нормальну площадку, тобто

Рис. 5.9

.

Енергія, яка переноситься через нормальну площадку ∆S за час ∆t, очевидно, рівна енергії, зосередженій в об’ємі циліндра висотою з основою ∆S (рис. 5.9), тобто

.

Тоді вектор густини потоку енергії , який називають вектором Умова, буде рівним

.

Середня енергія, що переноситься хвилею за одиницю часу через одиничну нормальну площадку, називається інтенсивністю хвилі І. Зрозуміло, що

, (5.65)

тобто інтенсивність хвилі пропорційна до квадрату амплітуди.