§ 5.8. Вимушені коливання

Для того, щоб в реальній коливній системі забезпечити незгасаючі коливання, необхідно постійно до неї підводити енергію ззовні. І тому розглянемо коливання матеріальної точки, на яку, крім квазіпружної сили і сили опору , діє додаткова періодична вимушуюча сила

,

де  – вимушуюча частота.

Тоді за другим законом Ньютона маємо

. (5.37)

Перепишемо рівняння (5.37) у вигляді

або

, (5.38)

де .

Розв’язок рівняння (5.38) будемо шукати як суму розвязку однорідного рівняння (5.29) і часткового розв’язку неоднорідного рівняння: . Для віддалених моментів часу . І тому

. (5.39)

Отже, вимушені коливання здійснюються з вимушуючою частотою ω. Для знаходження амплітуди А і початкової фази α продиференціюємо двічі (5.39):

(5.40)

Підставляючи (5.39) і (5.40) у (5.38), отримаємо:

а розкриваючи тригонометричні функції від складного аргументу:

(5.41)

Щоб рівняння (5.41) перетворилося в тотожність, потрібно, щоб суми коефіцієнтів при cos ωt в обох частинах рівності були рівні і суми коефіцієнтів при sin ωt в обох частинах були також рівні. Це означає, що

, (5.42)

. (5.43)

Із рівняння (5.43) отримаємо вираз для початкової фази вимушених коливань:

. (5.44)

Підносячи до квадрату рівняння (5.42) і (5.43) та складаючи отримані вирази, одержимо:

Звідси амплітуда вимушених коливань

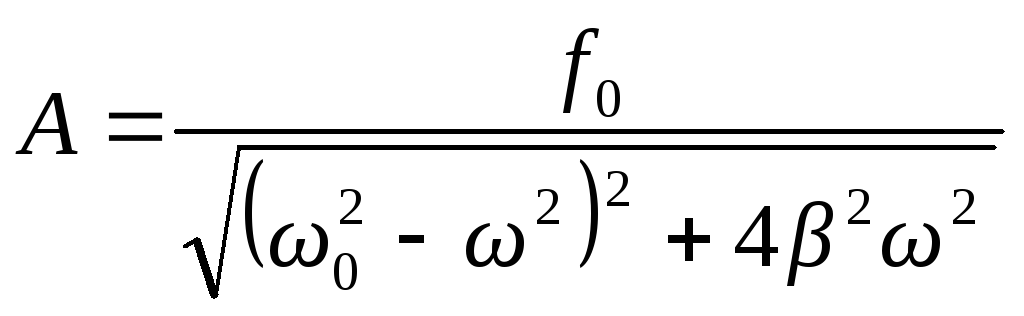. (5.45)

Проаналізуємо аналітично і графічно (рис. 5.7) залежність цієї величини від вимушуючої частоти  при різних значеннях коефіцієнту згасання β. Зокрема:

1) при ω → 0 А → А₀ =

2) при ω → ∞ А → 0

3) при ω → ω₀; β = 0 А → ∞

Досягнення максимального значення амплітуди вимушених коливань, коли вимушуюча частота ω наближається до власної частоти ω₀, називається резонансом.

Для знаходження резонансної частоти при знайдемо мінімум підкореневого виразу рівняння (5.45). Для цього прирівняємо до нуля похідну від цього виразу по :

.

Оскільки , то знаменник (5.45) досягає мінімуму при

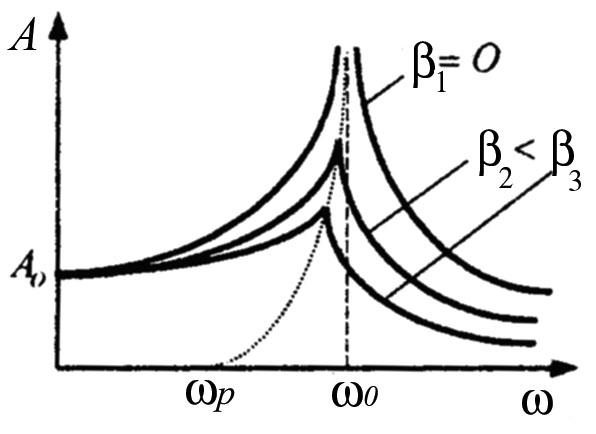Рис. 5.7

.

Отже, резонансна частота

.

Резонансна (максимальна) амплітуда досягає значення

.

Зрозуміло, що резонанс тим гостріший, чим менший коефіцієнт затухання. На практиці слід враховувати явище резонансу, оскільки в техніці він в одних випадках відіграє позитивну роль, а в інших – негативну.

§ 5.9. Поняття хвилі, рівняння хвилі. Поздовжні і поперечні хвилі. Фронт хвилі і хвильові поверхні. Довжина хвилі, хвильове число, фазова швидкість.

Хвиля – це процес поширення коливань у середовищі. Якщо коливання створити в деякій обмеженій частині середовища, то внаслідок наявності зв’язку між молекулами середовища коливання будуть охоплювати все середовище, тобто будуть поширюватись у середовищі.

Частинки середовища, в якій поширюється хвиля, не переносяться хвилею, вони лише здійснюють коливання навколо положення рівноваги. Хвилі, в яких частинки коливаються перпендикулярно до напрямку поширення хвилі, називаються поперечними. Хвилі, в яких частинки коливаються вздовж поширення хвилі, називаються поздовжніми. Поперечні хвилі поширюються в середовищах, де має місце деформація зсуву, тобто в твердих тілах. Поздовжні хвилі поширюються в середовищах, де має місце деформацію розтягу (розширення, стиску), тобто в газах, рідинах і твердих тілах.

Г

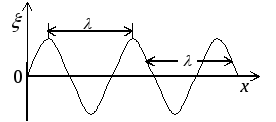Рис. 5.8

еометричне місце точок, до яких доходять коливання в момент часу t, називається фронтом хвилі. Геометричне місце точок, які коливаються в однаковій фазі, називається хвильовою поверхнею. Фронт хвилі весь час переміщується, а хвильові поверхні залишаються нерухомими (хвильових поверхонь існує безліч). Хвильові поверхні можуть бути довільної форми. Найпростіші хвильові поверхні мають вигляд сфер або площин. Тоді такі хвилі називаються сферичними або плоскими. Сферичні хвилі поширюються від точкових джерел, плоскі – від протяжних джерел.

Встановимо рівняння плоскої хвилі, що поширюється вздовж осі x. Це рівняння повинно виражати залежність змінної фізичної величини  (наприклад, зміщення коливної точки) від координати x і часу t:

.

Знайдемо вигляд ξ у випадку плоскої хвилі. Для спрощення вісь координат направимо вздовж напрямку поширення хвилі. Нехай точки джерела, що знаходиться при , коливаються за законом

.

До точки з координатою x (рис. 5.8) коливання прийдуть із запізненням на час

,

де v – фазова швидкість поширення хвилі, тобто швидкість переміщення фази хвилі. Тоді рівняння коливання в точці х буде мати вигляд

. (5.46)

Це і є рівнянням плоскої хвилі, яке часто записують у формі

(5.47)

де – хвильове число, – довжина хвилі.

Довжина хвилі λ – це шлях, який проходить хвиля за час, рівний періоду коливань, або відстань між найближчими точками, що коливаються в однаковій фазі (рис. 5.8). Відмітимо, що поняття плоскої хвилі передбачає постійність амплітуди, тобто нехтується поглинанням енергії середовищем.

Можна показати, що у випадку довільного напрямку поширення хвилі (наприклад, сферичної) рівняння хвилі має вигляд

, (5.49)

де – хвильовий вектор, – одиничний вектор нормалі до хвильової поверхні, – радіус-вектор хвильової поверхні (, – орти).

У комплексній формі рівняння хвилі (5.49) можна записати як

, (5.50)

де ; такий запис полегшує математичні перетворення.