3.2. Запасы устойчивости по частотным характеристикам

Среди частотных методов оценки запаса устойчивости, прежде всего, выделяются методы, связанные с амплитудно-фазо-частотной характеристикой разомкнутой системы, это запас устойчивости по модулю и запас устойчивости по фазе.

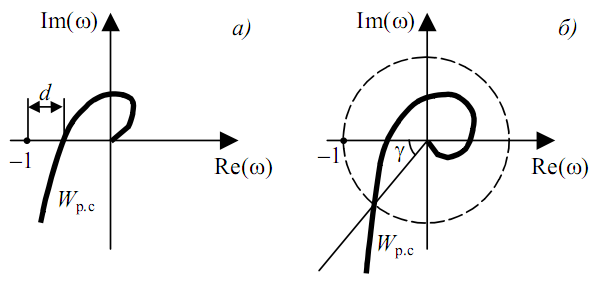
Запас устойчивости по модулю определяется как длина отрезка d, равного расстоянию от точки пересечения АФЧХ разомкнутой системы с отрицательной вещественной полуосью до точки (-1, j0).

Численно запас устойчивости по модулю показывает, на сколько должен измениться модуль АФЧХ разомкнутой системы, чтобы система вышла на границу устойчивости.

Запас устойчивости по фазе − это угол , лежащий между вещественной отрицательной полуосью и лучом, проведенным из начала координат в точку пересечения АФЧХ с единичной окружностью с центром в начале координат.

Численно запас устойчивости по фазе показывает, на сколько должно увеличиться отставание по фазе в разомкнутой системе при неизменном модуле АФЧХ, чтобы система вышла на границу устойчивости.

Как правило, эти показатели используют вместе.

Частотные методы оценки запаса устойчивости: а − запас устойчивости по модулю; б − запас устойчивости по фазе

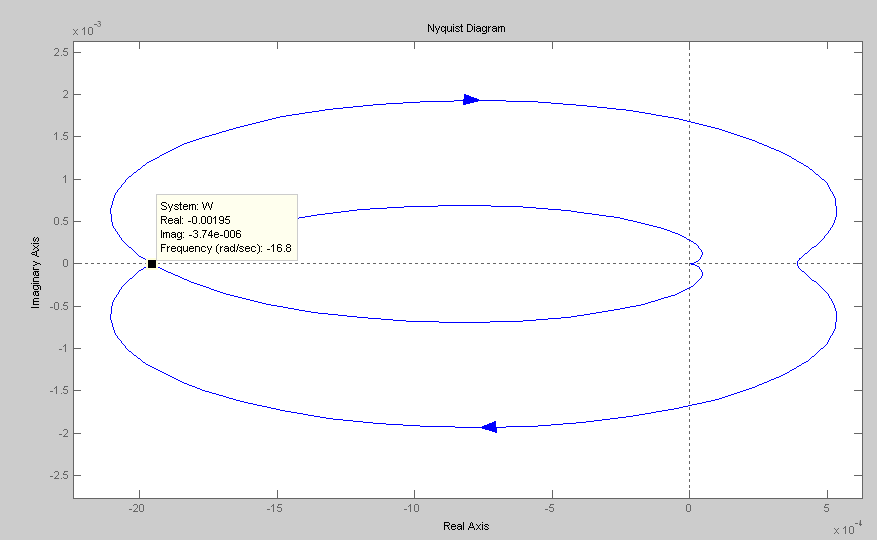
4. Исследование точности сау

При исследовании систем автоматического управления приходится решать задачу обеспечения требуемых показателей качества, характеризующих точность и плавность протекания процесса:

• быстродействия;

• колебательности;

• перерегулирования;

4.1 Построение переходного процесса по управляющему воздействию

Любое изменение переменных состояния динамической системы X(t), вызванное приложением внешнего воздействия f(t) или не нулевыми начальными условиями, называется переходным процессом.

В данном случае переходный процесс в системе является её реакцией на внешнее (управляющее) воздействие, которое в общем случае может быть сложной функцией времени. Чаще всего прямые оценки качества получают по кривой переходной характеристики h(t), т.е. при воздействии единичной ступенчатой функции и нулевых начальных условиях.

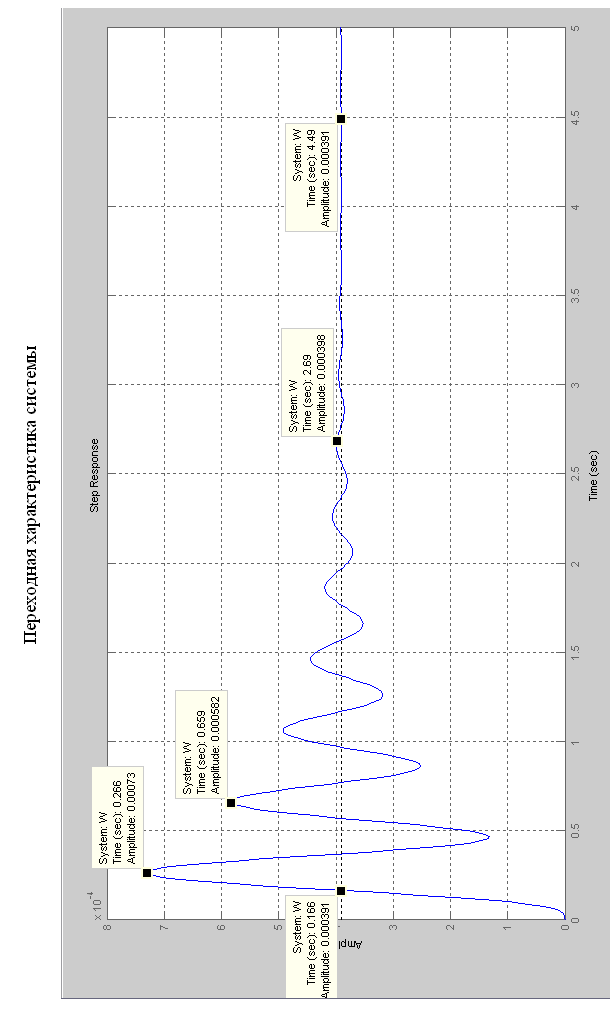
4.2. Оценка качества переходного процесса при воздействии единичной ступенчатой функции.

Перерегулирование – максимальное отклонение переходной характеристики от установившегося значения выходной величины, выраженное в относительных единицах или процентах.

,

Время достижения 1-го максимума:

Время регулирования – минимальное время, по истечении которого регулируемая величина будет оставаться близкой к установившемуся значению с заданной точностью.

при

или ,

Пусть 2

2,69 Сек

Число колебаний , которое имеет переходная характеристикаилиза время регулирования. При проектировании систем чаще всего допускают, а иногда и до, но в некоторых случаях колебания в системе недопустимы.

В нашем случае за время регулирования 2,69 сек число колебаний

Время нарастания переходного процесса – абсцисса первой точки пересечения кривой переходной характеристикис уровнем установившегося значенияили кривой отклоненияс осью абсцисс.

сек

Декремент затухания , равный отношению модулей двух смежных перерегулирований: