1. Принципиальная схема автоматической системы регулирования с двумя усилителями

На рис. 1 изображена принципиальная схема исследуемой системы автоматического регулирования с двумя усилителями.

Рис. 1 Принципиальная схема автоматической системы регулирования

Данная система регулирования работает по следующему принципу, допустим, что частота вращения ротора турбины увеличилась. Тогда шары регулятора скорости 1 под действием центробежной силы пойдут вверх, муфта регулятора устремиться вверх. Через рычаг сигнал передастся на золотник 2, поршни которого пойдут вниз. В результате откроются нижние окна золотника 2, и масло устремит поршень усилителя 3 вверх. При этом откроются верхние окна золотника 4, и масло устремит поршень усилителя 5 вниз, тем самым, прикрывая клапан турбины 6. Через рычаги обратной связи система приходит в состояние равновесия.

2. Решение системы дифференциальных уравнений сар

Уравнения движения отдельных элементов системы автоматического регулирования:

1. Уравнение движения ротора:

,

.

2. Уравнение движения поршня 1-го сервомотора:

,

.

3. Уравнение движения 1-го золотника:

, где коэффициент выключения таким образом

.

4. Уравнение движения поршня 2-го сервомотора:

,

.

5. Уравнение движения 2-го золотника:

, где коэффициент выключения таким образом

6. Уравнение регулятора скорости:

,

.

В результате имеем систему из 3-х дифференциальных уравнений:

,

,

;

Подставляя известные величины, получим:

,

,

.

Составим характеристическое уравнение для этой системы через определитель:

Исследуем устойчивость системы по методу Рауса-Гурвица:

• для устойчивой динамической системы все коэффициенты характеристического уравнения должны быть положительными;

• для устойчивости динамической системы необходимо также, чтобы определители до порядка n-1 были положительными.

С₀=0,02>0; С₁=0,21>0;C₂=1>0;C₃4,545>0.

1-й определитель: С₁=0,21>0;

2-й определитель: С₁С₂-С₀С₃=0,211-0,024,5450,1191>0.

Итак, в данном случае динамическая система устойчива.

Определим характер переходного процесса по диаграмме Вышнеградского [2] (см. рис. 2). Для этого найдем координаты XиY, которые являются комплексами из известных постоянных коэффициентов характеристического уравнения:

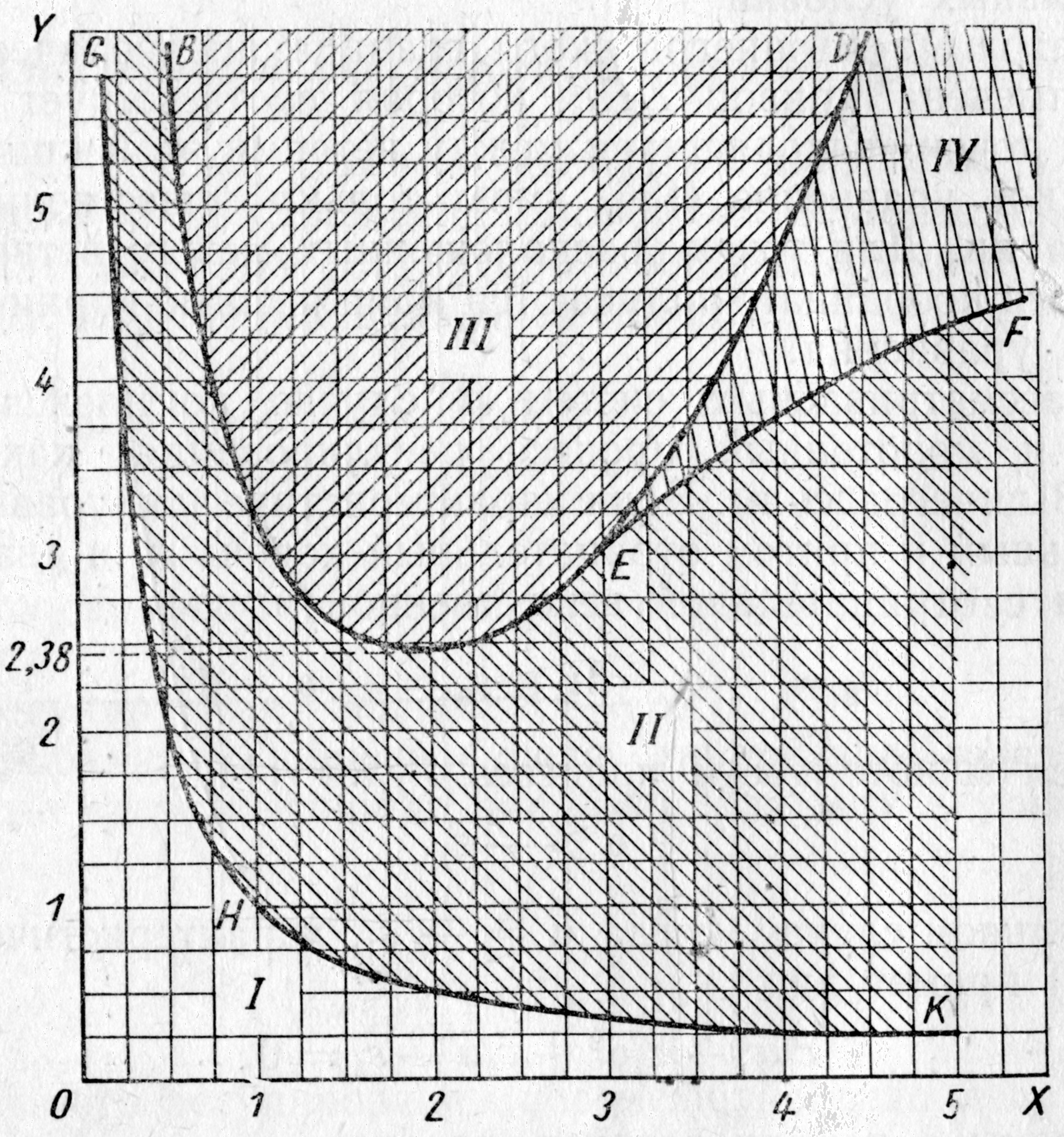
Рис.2 Диаграмма Вышнеградского:

I– областьнеустойчивого регулирования;II– область устойчивых колебательных процессов;III– область монотонных процессов;IV– область апериодических процессов.

В результате получаем, что данный процесс лежит в области II устойчивых колебательных процессов.

Определим динамический заброс и логарифмический декремент колебаний по диаграммам ЦКТИ [1] (рис. 3 и рис. 4). Диаграммы построены в зависимости от следующих комплексов:

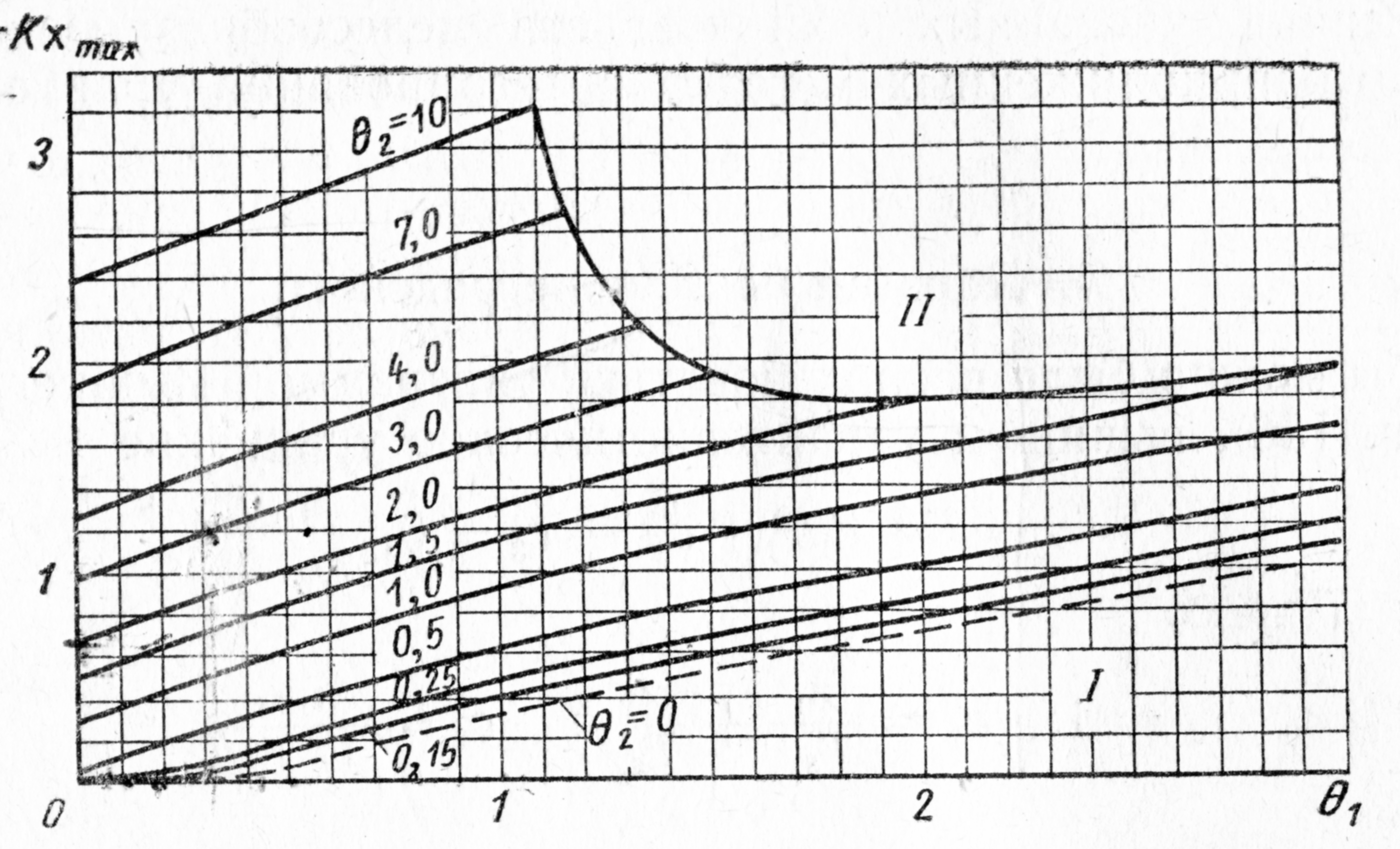
Рис. 3 Перерегулирование для системы с двумя усилителями:

I – область устойчивого регулирования; II – область неустойчивого регулирования.

Рис. 4 Логарифмический декремент колебаний для схемы с двумя усилителями.

Получаем, что:

1. динамический заброс (по диаграмме) φ_max = - 0,3.

2. логарифмический декремент колебаний (по диаграмме) d = 3.

3. Анализ динамических качеств системы и рекомендации,

направленные на улучшение динамики исследуемой системы

регулирования

Чтобы уменьшить динамический заброс и увеличить логарифмический декремент колебаний необходимо уменьшать оба комплекса ₁ и ₂, данный вывод можно сделать, проанализировав графики изображенные на рис. 3 и рис. 4.

Рассмотрим пути уменьшения данных комплексов:

1. Уменьшить времена усилителей Т_s1 и Т_s2.

Для этого обратимся к зависимости , здесь нужно искать возможность по уменьшениюFиm_maxи по увеличению ширины и высоты окон золотникаbиSсоответственно, а также давления нагнетания маслаp_н. Но увеличениеbиSограничено увеличивающейся силой реакции масла, вытекающего из золотника, поэтому необходимо предусмотреть мероприятия по уменьшению этой силы, например, выполнить подрезку пояска золотника. А увеличение давления нагнетания масла ограниченно прочностью трубопроводов.

2. Увеличить коэффициент неравномерности , но он обычно задан в зависимости от задач регулирования, характеризует наклон статической характеристики.

3. Увеличить время ротора Т_а, которое в свою очередь зависит от геометрических размеров ротора, которые обычно заданы.

4. Расчет на ЭВМ характеристик переходного процесса

На ЭВМ произведен расчет системы дифференциальных уравнений, описывающих динамику данной системы регулирования. В качестве основного программного обеспечения используется программно-методический комплекс МИК-АЛ [3]. Результат расчета представлен в виде графика (рис. 5).

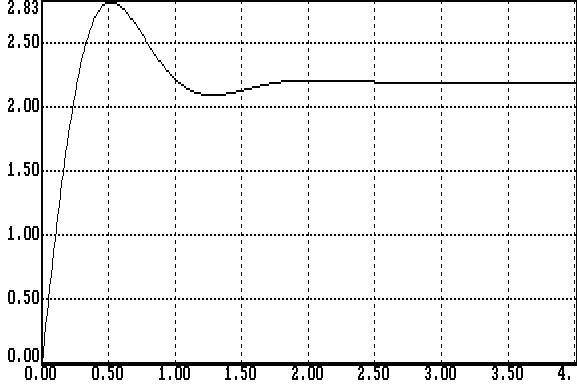
Рис.5  = f(t)

По графику, изображенному на рис. 5 найдём динамический заброс, используя формулу:

относительный динамический заброс = -’_max/₀, где

₀=0,218 и ’_max=0,065, откуда

относительный динамический заброс = - 0,065/0,218 = - 0,298.

По этому же графику найдем логарифмический декремент колебаний, который вычисляется по формуле:

d = ln(’_max/”_max), где

”_max=0,003, тогда

d=ln(0,065/0,003)=3,08.

Время переходного процесса Т= 0,83 с. (см. рис. 5).

Полученные результаты вполне приемлемы (см. расчёт выше п. 2).