курсовая работа / opredelit_ustoychivost_zamknutoy_sledyashey_sistemy

Министерство образования и науки Украины

_____________________________________________________

Контрольная работа №_____

по предмету: ________________

на тему: _______

студента __ курса,

группы_

заочного факультета

_________

___________

_________

Шифр:_______

Дата отсылки в вуз:____________

Рецензент____________________

Задание на контрольную работу

1. Определить устойчивость замкнутой следящей системы (рис. 1) по критерию устойчивости Гурвица.

2. Используя логарифмический критерий устойчивости Найквиста, определить устойчивость замкнутой следящей системы.

3. Вычислить первые три коэффициента ошибки, а также добротность по скорости следящей системы.

Варианты числовых значений исходных данных приведены в таблице 1

Таблица 1- Варианты числовых значений исходных данных

№ п/п	Ту, с	Тм, с	К1, В/град	К2	К3, град/(В*с)	К4, град/(Н*см*с)	К5
1	0,010	0,20	1,00	100	0,15	0,30	0,001

Рис. 1 – Структурная схема следящей системы

1. Арифметический критерий Гурвица

Свойства устойчивости проявляются в способности системы возвращаться в первоначальное состоянии или близкое к нему при приложении к системе или снятии воздействия. В связи с этим различают три ситуации: 1) система устойчива; 2) система неустойчива; 3) система "безразличная", нейтральная.

Оценить устойчивость системы можно в результате исследования ее математической модели, то есть решить соответствующую систему дифференциальных уравнений.

Для разомкнутой системы математическая модель в операторной форме:

, или , где - оператор дифференцирования.

Для замкнутой системы:

, или . Если (единичная обратная связь), то .

На основании характеристического уравнения системы

. (1.1)

строится определитель Гурвица (при ).

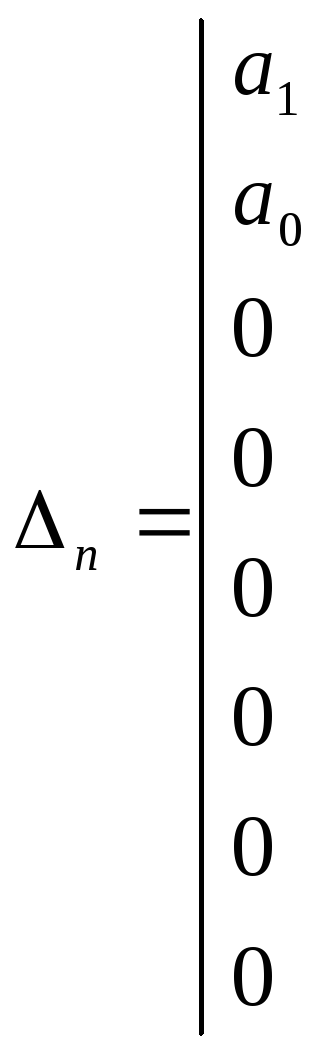
(1.2)

Свободные места заполняются нулями.

Для устойчивости системы необходимо и достаточно, чтобы определитель Гурвица и все его диагональные миноры были положительны.

Диагональные миноры:

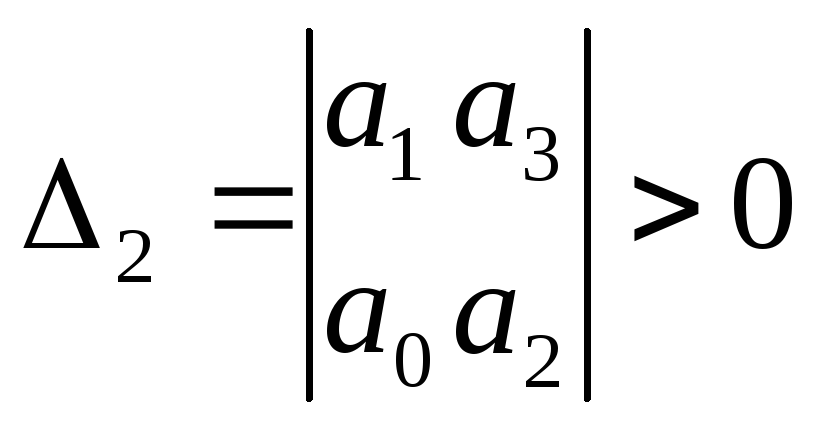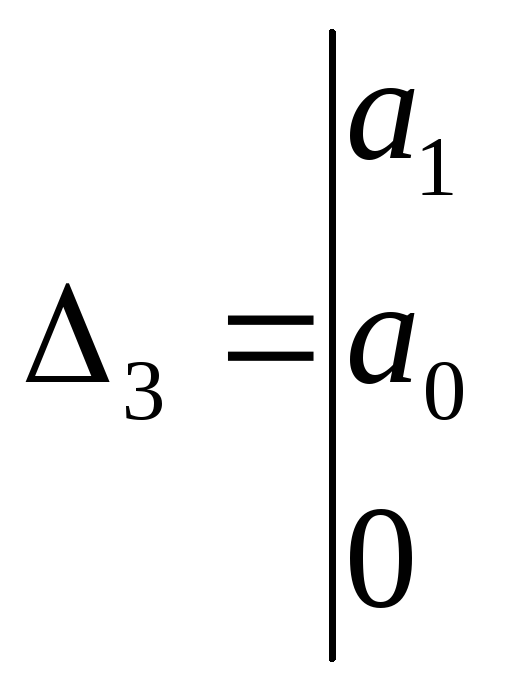
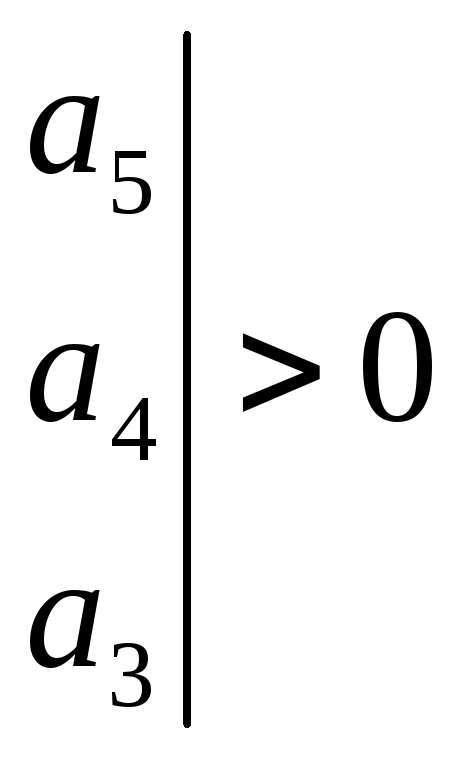; ; ; (1.3)

Из найденного в контрольной работе 1 соотношения имеем следующий характеристический полином:

D(p) ==

(0.01p²+p)(0.2p+1)+4.5=0.002p³+0.21p²+p+1 (1.4)

Таким образом, по (1.4) коэффициенты характеристического полинома равны:

а₀=0,002

а₁=0,21

а₂=1

а₃=1

n = 3 => уравнение динамики: a₀p³ + a₁p² + a₂p + a₃ = 0.

Определители Гурвица:

Δ₁ = a₁ > 0,

Δ₂ = a₁a₂ - a₀a₃ > 0,

Δ₃ = a₃Δ₂ > 0.

Условие устойчивости:

a₀ > 0,

a₁ > 0,

a₂ > 0,

a₃ > 0,

a₁a₂ - a₀a₃ > 0,

Выполнив ручной просчет, получим следующие результаты:

Определители Гурвица:

а₁=0,21, Δ₁ = a₁ > 0,

0,21*1-0,002*1=0,208, Δ₂ = a₁a₂ - a₀a₃ > 0,

0,208*1=0,208, Δ₃ = a₃Δ₂ > 0.

Условие устойчивости:

а₀=0,002, a₀ > 0,

а₁=0,21, a₁ > 0,

а₂=1, a₂ > 0,

а₃=1, a₃ > 0,

0,21*1-0,002*1=0,208, a₁a₂ - a₀a₃ > 0.

По критерию Гурвица, система слежения устойчива.

2. Логарифмический частотный критерий Найквиста

Из критерия Найквиста известно, что САУ, находящаяся на апериодической границе устойчивости в разомкнутом состоянии, станет устойчивой при ее замыкании, если годограф АФЧХ не охватывает на комплексной плоскости "точку Найквиста" (-1, 0(i)). Поэтому рассмотрим более внимательно поведение линии годографа в окрестности точки (-1, 0·i).

Построение годографа выполним по данным из табл. 4.1 контрольной работы №1 (здесь – табл. 2.1):

Таблица 2.1 – АФХ системы

ω	1,002305	1,023293	1,258925	10		1010	10100	101000
lg(ω)	0,001	0,01	0,1	1		10	12,5893	15,8489
A(ω)	1	0,999998	0,99982	0,982437		0,453898	0,369068	0,29305
lg(ω)	19,9526	25,1189	31,6228	39,8107		50,1187	63,0957	100
A(ω)	0,2271	0,171318	0,125278	0,0883814		0,059906	0,0389108	0,0144248
lg(ω)	1000	10000	10000
A(ω)	2,23605E-5	2,24986E-8	2,24986E-8

(-1, 0·i)

Рис. 2.1 – Годограф Найквиста

(-1, 0·i)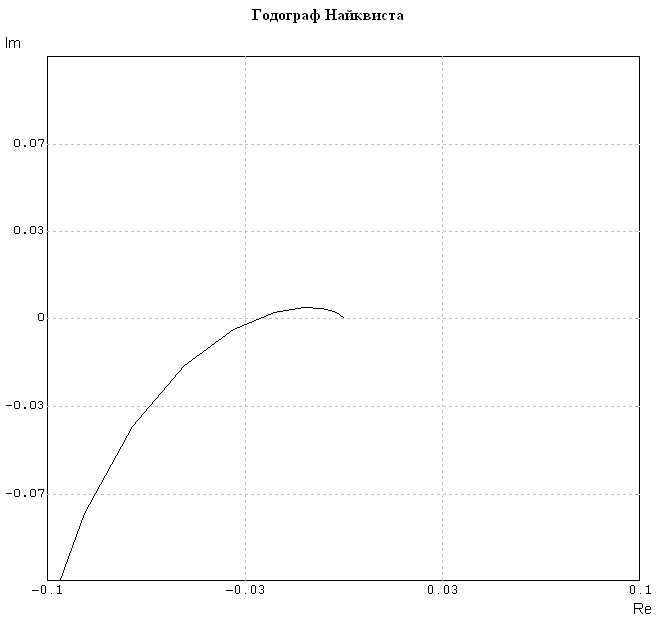

Рис. 2.2 – Годограф Найквиста (увеличение)

Так как линия годографа разомкнутой САУ на рис. 2.1 и 2.2 без сомнения не охватывает точку (-1, 0·i), то исходная САУ в замкнутом состоянии будет устойчива. 

3. Вычисление первых трех коэффициентов ошибки, а также добротность по скорости следящей системы

Представим передаточную функцию в виде

. (3.1)

В разложении ошибки по производным входного воздействия

(3.2)

заменим операцию дифференцирования символом р, т.е. = p и вынесем формально общий множитель за скобки:

(3.3);

С другой стороны можно определить дифференциальным уравнением, записанным в сокращенной форме:

. (3.4)

Подставив (3.1) в (3.4), приравняем выражения (3.3) и (3.4) 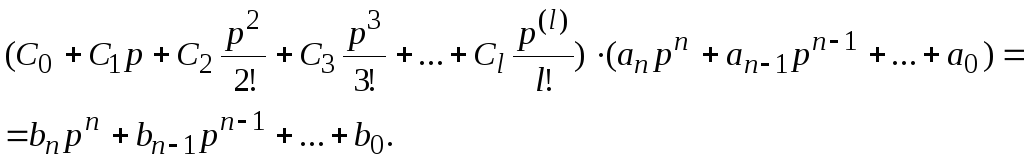(3.5)

Приравняв слагаемые, имеющие одинаковые степени р в правой и левой частях (3.5), получим:

; ;

;

; .

На основании полученных выражений можно записать формулу для расчета коэффициентов ошибки:

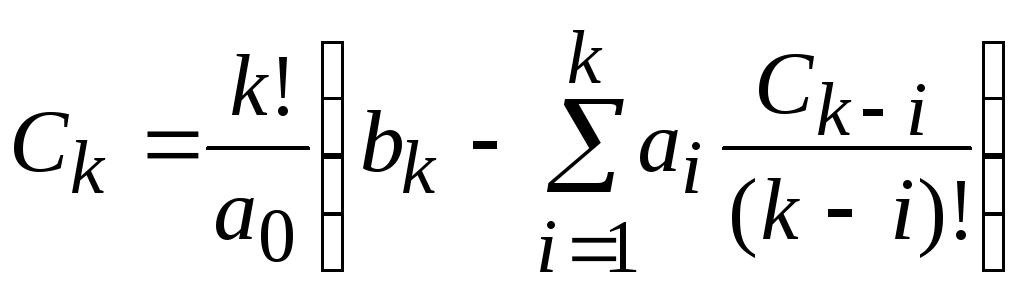. (3.6)

Коэффициенты ошибки могут быть также вычислены по формулам, составленным из коэффициентов полиномов числителя и знаменателя передаточной функции разомкнутой системы:

(3.7)

где k – добротность системы; v – порядок астатизма.

Для вычисления данных коэффициентов разложим в ряд передаточную функцию замкнутой системы по ошибке, и первые три члена этого разложения (в порядке убывания степеней) и будут искомыми коэффициентами.

В ходе контрольной работы 1 было получено следующее выражение для передаточной функции замкнутой системы по ошибке:

(3.8)

Разложим в (3.8) ряд Тейлора:

(3.9)

где - остаточный член 3-го порядка.

Тогда первые три коэффициента ошибки будут иметь следующие значения:

С₀=1,

С₁=0,0099,

С₂=1,527*10^-5.

Расшифруем физический смысл полученных коэффициентов.

- коэффициент ошибки по положению;

- коэффициент ошибки по скорости;

- коэффициент ошибки по ускорению.

Исходя из полученного значения С₁=0,0099, видим, что добротность данной системы слежения довольно высока: ошибка по скорости не превышает 1%.

9