1.10 Определение устойчивости системы по критерию Михайлова

Характеристическое уравнение системы имеет вид уравнения (1).

Согласно критерию Михайлова общий вид характеристического уравнения должен иметь следующий вид:

, где .

Таким образом, чтобы исследовать систему автоматического управления по критерию Михайлова необходимо разделить все коэффициенты характеристического уравнения (1) на 7 получим:

= 0

. (2)

В характеристическом уравнении (2) произведем замену и получим характеристический вектор:

Выделим вещественную и мнимую части:

,

где – вещественная часть;

– мнимая часть.

Для построения годографа Михайлова воспользуемся программой Mathcad.

Рисунок 8 – Годограф Михайлова для системы статического регулятора

уровня прямого действия

Для устойчивости системы необходимо и достаточно, чтобы годограф Михайлова при изменении частоты от нуля до бесконечности повернулся против часовой стрелки, начиная с вещественной оси на число квадрантов равное порядку характеристического уравнения, последовательно проходя эти квадранты.

Таким образом, из рисунка видно, что годограф Михайлова системы четвертого порядка при изменении частоты от нуля до бесконечности представляет собой линию, которая начинается на вещественной оси и заканчивается в четвертом квадранте, следовательно, система является устойчивой.

1.11 Построение переходного процесса

Переходная функция - это реакция системы на ступенчатое входное воздействие. Для того, чтобы построить переходный процесс, используем обратное преобразование Лапласа от функции вида .

Передаточная функция САУ имеет вид:

Для построения графика переходного процесса воспользуемся программой Маthcad.

Максимальное значение переходного процесса: h_max=0,07

Установившееся значение переходного процесса: h_уст=0,05

Время переходного процесса - время регулирования системы; определяется как интервал времени от момента приложения какого-либо воздействия до времени вхождения в пятипроцентную трубку (). t_перех=7,5 c.

Значение перерегулирования:

.

Время достижения макс. значения переходного процесса: t_max=1,6 с.

Время первого согласования - время, за которое регулируемая величина первый раз достигает своего установившегося значения. =9,3 с.

Колебательность n – число колебаний системы от момента воздействия на нее до перехода в установившееся состояние. n=2.

, с

Рисунок 9 – График переходного процесса для системы статического ре-

гулятора уровня прямого действия

1.12 Построение амплитудно-частотной характеристики

Косвенные оценки качества системы управления определяются из графика амплитудно-частотной характеристики.

Для построения графика АЧХ необходимо сначала в передаточной функции САУ заменить , получим:

Определим выражение для амплитудно-частотной характеристики и построим её график.

A_max

ω_р

ω_ср

, Гц

Рисунок 10 - График АЧХ системы статического регулятора уровня пря-

мого действия

Из графика АЧХ определим косвенные характеристики:

– максимальная амплитуда;

– амплитуда при нулевой частоте;

Показатель колебательности ;

– резонансная частота (частота, при которой АЧХ достигает максимального значения);

– частота среза;

– полоса пропускания (полоса, при которой значение амплитуды больше, чем );

=3,6 – период колебаний;

– величина перерегулирования;

=7,22 с, =10,83 с – время регулирования.

с

1.13 Определение запаса устойчивости

Для определения запасов устойчивости по фазе и по амплитуде необходимо построить графики ЛАЧХ И ЛФЧХ на одних и тех же осях, причем ЛФЧХ строится ниже ЛАЧХ.

Передаточная функция разомкнутой системы:

График ЛАЧХ строим по следующей функции:

.

График ЛФЧХ строим по следующей формуле:

.

Для построения графиков воспользуемся программой Matlab.

ΔL

Δφ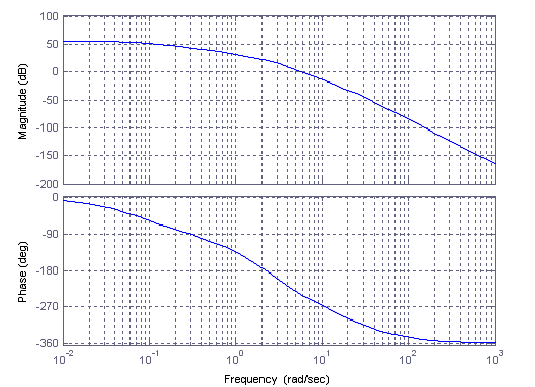

Рисунок 11 - Графики ЛАЧХ и ЛФЧХ

Определим запасы устойчивости по фазе (φ) и по амплитуде (L):

Δφ = 63.8⁰;

Аппроксимируем ЛАЧХ, изображенную на рисунке 11:

ω₁

ω₂

0 Дб/дк

-20 Дб/дк

-40 Дб/дк

ω, Гц

Рисунок 12 – Аппроксимация ЛАЧХ

Из рисунка видно, что передаточная функция в общем виде имеет вид:

Для того, чтобы записать полученную передаточную функцию системы в численном виде, необходимо рассчитать T₁, T₂, по формуле:

Частота находится из рисунка 12. Для того чтобы её определить, нужно опустить перпендикуляр с точки пересечения аппроксимированных участков.

Таким образом, из рисунка видно, что 0,13, 5,1,

Следовательно, передаточная функция системы в численном виде будет иметь вид:

2 Исследование НЕлинейной части системы

2.1 Техническое задание для нелинейной части системы

НЭ – нелинейный элемент;

W₂ (p) - передаточная функция бака;

W₃ (p) - передаточная функция насоса;

W₄ (p) - передаточная функция поплавка;

W₅ (p) - передаточная функция рычага.

Рисунок 13 – Структурная схема нелинейной системы

Передаточная функция бака:

W₂(р) = k / Тр+1= 3/13р+1.

Передаточная функция насоса:

W₃ (р) = k / (Т₁р+1)(Т₂р+1) =4/(0,4р+1)(0,04р+1).

Передаточная функция поплавка:

W₄(р) = k / Тр+1 = 5/0,5р+1.

Передаточная функция рычага:

W₅(р) = k = 5.

Графическая характеристика нелинейного элемента:

Рисунок 14 – Релейная статическая характеристика нелинейного элемента

2.2 Упрощение нелинейной системы

Для построения фазового портрета упростим структурную схему нелинейной системы управления. Разомкнем систему перед нелинейным элементом.

Выражение для общей передаточной функции линейной части:

Общая схема системы статического регулятора прямого действия, включая нелинейный элемент примет вид:

НЭ

W­(p)

Рисунок 15 - Вид структурной схемы, включающей линейную и нелинейную части

Так как обратная связь оказывает на состояние системы незначительное воздействие, то в дальнейшем будем рассматривать систему без нее:

2.3 Построение фазового портрета нелинейной системы

Об устойчивости системы будем судить по фазовому портрету. Построение фазового портрета будем вести методом припасовывания. Но, сначала рассмотрим данную нам нелинейную характеристику элемента с ограничениями.

Передаточная функция есть или ,

где -передаточная функция линейной системы;

Подставляя в эту формулу значение передаточной функции получим:

Для того чтобы построить фазовый портрет, необходимо, чтобы степень числителя и знаменателя не превышала вторую степень и наше уравнение не удовлетворяет этим условиям.

Степени больше второй - степени для более низких частот, оказывают небольшое влияние на систему в целом, поэтому мы можем ими пренебречь.

Следовательно можем записать, что:

Приведённую формулу можно записать в виде:

Введем замену :

Перенесем влево:

Так как в качестве нелинейного элемента используется реле со статической характеристикой, представленной на рис.14, то подставляя значение для трех участков, получим систему:

Создадим матрицу для решения дифференциального уравнения в программе MathCad:

В данной матрице реализовано условие перехода от одного уравнения к другому. Зададим матрицы для трех начальных условий:

Возьмем количество точек равным 500 и конечное время интегрирования 100, то матрица решений запишется как:

Построим фазовый портрет:

Рисунок 16 – Фазовый портрет нелинейной системы

Построим переходные процессы нелинейной системы:

Рисунок 17 – Переходный процесс нелинейной системы

Из графика видно, что при различных начальных условиях система будет оставаться устойчивой. С течением времени процесса амплитуда колебаний будет уменьшаться, система придет к устойчивому равновесию. Устойчивость системы подтверждает график переходного процесса рисунок 17.