3. Расчет времени установления процесса на выходе

;

;

;

сек.

4. Проектирование пропорционального регулятора, обеспечивающего 3 % статической ошибки от установившегося значения

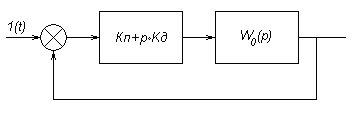
Передаточная функция разомкнутой системы, состоящей из объекта управления и П-регулятора, соединенных последовательно, в соответствии с [2]:

;

Передаточная функция замкнутой системы [3]:

;

Установившееся значение переходной функции замкнутой системы [3]:

;

Статическая ошибка замкнутой системы [3]:

;

Установившееся значение статической ошибки замкнутой системы [3]:

.

Для обеспечения 3 % статической ошибки от установившегося значения, необходимо выполнение равенства:

.

Построим переходную характеристику замкнутой системы.

.

По формуле Хэвисайда:

.

;;

;

.

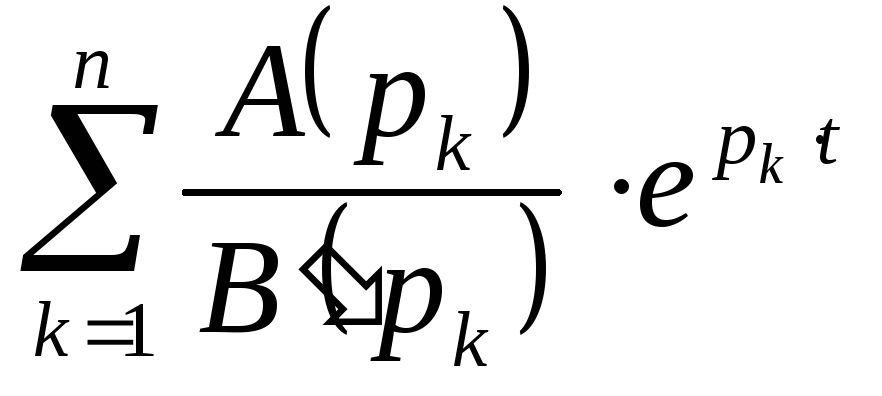Рис.2. Переходная характеристика замкнутой системы

Рассчитаем время регулирования из условия вхождения в 3-х процентную трубку.

;

;

сек.

5. Проектирование пропорционально-дифференциального регулятора, обеспечивающего время переходного процесса, по крайней мере, в 2 раза меньше, чем в предыдущем пункте

Передаточная функция ПД-регулятора: .

Передаточная функция разомкнутой системы:

;

Передаточная функция замкнутой системы:

.

Найдем по формуле Хэвисайда:

;;

;

.

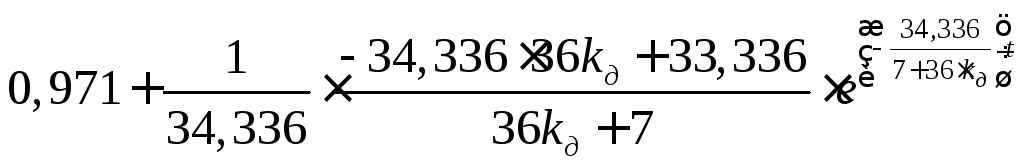Коэффициент выбирается из условия. Примемсек.

Из условия вхождения в 3-х процентную трубку: .

.

С помощью пакета MathCADрешили данное уравнение, получили ответ.

Итак, передаточная функция ПД-регулятора, необходимого для обеспечения времени переходного процесса, равного 0,358 сек: .

Переходная характеристика замкнутой системы, состоящей из объекта управления и ПД-регулятора:

;

Ширина 3-х процентной трубки:

Ширина 3% трубки

Рис.3. Переходная характеристика замкнутой системы с ПД-регулятором

6. Изменение найденного значения коэффициента при дифференциальной составляющей на 10% и оценка влияния этого коэффициента на время регулирования

1);

=.

Время регулирования из условия вхождения в 3-х процентную трубку:

;

сек.

2);

=

Время регулирования:

сек.

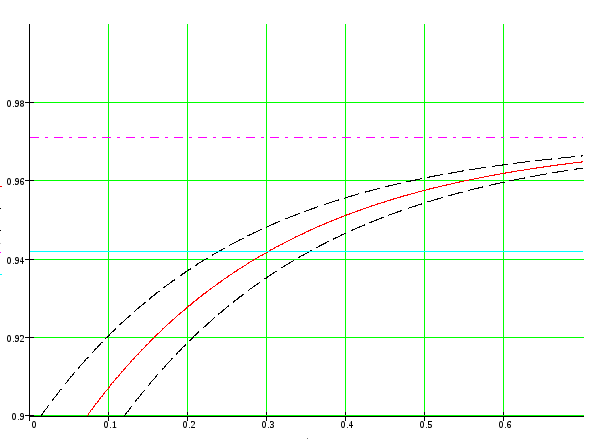
Рис.4. Переходная характеристика замкнутой системы с ПД-регулятором при различных значениях коэффициента при дифференциальной составляющей

Из графика видно, что изменение коэффициента при дифференциальной составляющей существенным образом повлияло на время регулирования. В частности, в нашем случае, при уменьшении коэффициента всего на 10 %, время регулирования увеличилось. А при увеличении его на 10 % время регулирования уменьшилось.

7. Проектирование пид-регулятора таким образом, чтобы корни характеристического уравнения замкнутой системы были бы действительными

Передаточная функция регулятора: .

Передаточная функция разомкнутой системы:

.

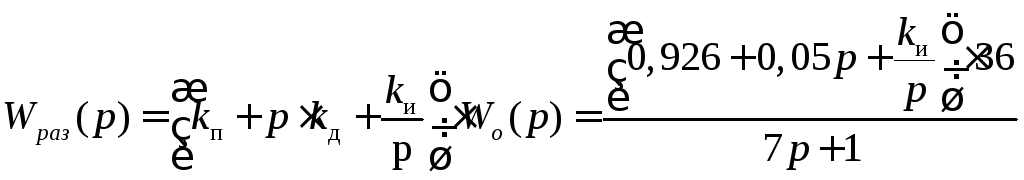Передаточная функция замкнутой системы имеет вид:

;

Характеристическое уравнение передаточной функции замкнутой системы:

= 0;

Для того чтобы корни характеристического уравнения были действительными: D0.

Кроме того, для того, чтобы система была устойчивой, корни характеристического уравнения должны находиться в левой полуплоскости (должны быть отрицательными): .

;.

, что и так уже предусмотрено.

Примем = 5. Тогда характеристическое уравнение примет вид:

= 0.

;

;

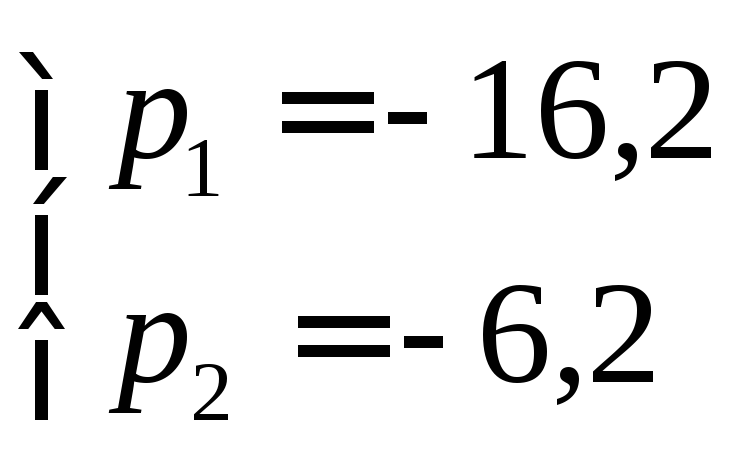
Таким образом, получили ПИД-регулятор с передаточной функцией .