Лекция № 18.

АНАЛИЗ ДИСКРЕТНЫХ ЛИНЕЙНЫХ СИТЕМ МПС.

План лекции:

1. Вычисление z- ПФ многомерных систем.

2. Пример вычисления z- ПФ силовой системы привода.

3. Исследование устойчивости дискретных систем.

4. Вычисление переходных процессов в импульсных системах.

18.1. Вычисление z- пф многомерных систем.

Рассмотрим уравнение состояния линейной многомерной дискретной системы:

x[k+1]=Фx[k]+Hu[k] (18.1)

y[k]=сx[k]+Ru[k] (18.2)

Здесь x=(x₁,...x_n)- n-мерный вектор переменных состояния;

u=(u₁,...u_m)- m- мерный - вектор входных воздействий;

y=(y₁,...y_r)- r-мерный вектор выходных переменных.

Использование математического описания в форме (18.1), (18.2) дает ряд преимуществ при исследовании дискретных систем с вычислительной точки зрения. В частности оно позволяет легко формализовать решения задач анализа и синтеза ИС.

Например, математическое описание (18.1), (18.2) может быть использовано для матричной z- передаточной функцией, устанавливающей связь между входными и выходными переменными. Найдем эту z- передаточную функцию.

Введем z- преобразование координат:

x(z)=Z{x[k]}, y(z)= Z{y[k]}, u(z)= Z{u[k]}.

Применяя z- преобразование к обеим частям уравнений (18.1), (18.2) получим:

,

откуда:

(zE-Ф)x =H u+zx(0);

x =(zE-Ф)^-1 Hu +(zE-Ф)^-1 zx(0);

y =c(zE-Ф)^-1 Hu +c(zE-Ф)^-1 zx(0)+Ru(z) =

=[ c(zE-Ф)^-1 H+R] u + c(zE-Ф)^-1 zx(0) (18.3)

Положив в (5.29) , получим зависимость:

y =[ c(zE-Ф)^-1 H+R] u ,

устанавливающую связь между операторными изображениями входа и выхода. Матрица z- передаточных функций, связывающая входные переменные u₁, u₂,... u_m с выходными переменными y₁, y₂,... y_r, определится соотношением:

.

Для системы с m- выходами и r- входами матричная ПФ имеет размерность rх m, причем W_ij(z) представляет собой z- ПФ от j- того входа к i- тому выходу.

Рассмотрим вычисление матричной ПФ. Основная трудность заключается в определении обратной матрицы (zE-Ф)^-1. Аналитическое выражение для ее вычисления имеет вид:

,

где - присоединенная (взаимная) матрица (напомним, что это транспонированная матрица алгебраических дополнений элементов исходной матрицы).

Из приведенной зависимости, в частности, видно, что det(zE-Ф) - входит в матрицу передаточных функций. Этот детерминант определяет характеристическое уравнение системы:

Det (zE-Ф)=0.

Корни этого уравнения являются собственными числами матрицы Ф.

Таким образом, матричная z- ПФ содержит в качестве своих полюсов собственные числа матрицы Ф.

Алгоритмы получения ПФ, основанные на использовании уравнений состояния, удобнее алгоритмов, построенных на формулах - преобразования. Использование ЭВМ в задачах исследования дискретных систем позволяет применить стандартные программы обращения матриц, что приводит к существенному снижению трудоемкости выполняемых вычислений.

Пример вычисления z-ПФ силовой системы привода:

Введем обозначения:

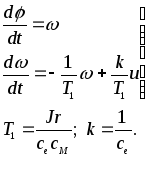
где - угол поворота вала двигателя;

- скорость;

21. управляющее напряжение;

k и T₁ - параметры ОУ.

Выберем вектор состояния . Тогда

.

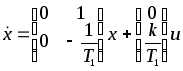Применим для вычисления переходной матрицы Ф - аналитический способ, основанный на использовании преобразования Лапласа.

,

при этом

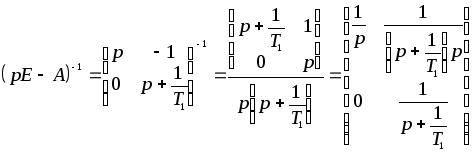
Найдем обратное преобразование:

(18.4)

Подставляя в (18.4) t=T (интервал квантования), получим переходную матрицу состояния дискретной системы:

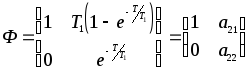
Перейдем к нахождению z- ПФ. Пусть y[k]=x[k], то есть e=E, R=0.

Тогда выражение для матричной ПФ примет вид:

.

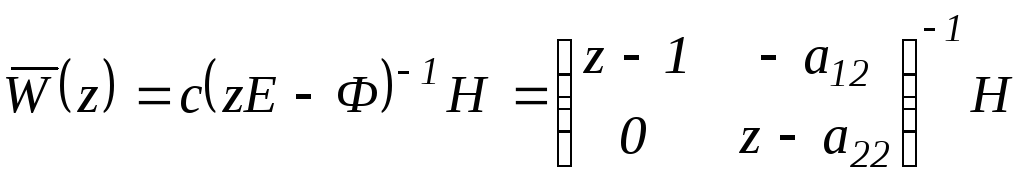Для определения элементов матрицы H найдем решение дифференциальных уравнений объекта при нулевых начальных условиях и u=1:

Подставив в полученные зависимости t=T, найдем матрицу H:

.

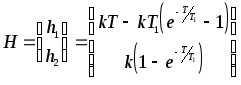Матрица ПФ в данном случае характеризует связь напряжения u с координатами . Вычислим матрицу:

.

окончательно получим:

.
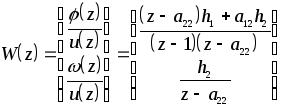