Наибольшее и наименьшее значения функции двух переменных
При нахождении наибольшего и наименьшего значений функции нескольких переменных, непрерывной на некотором замкнутом множестве, следует помнить, что эти значения достигаются в точках экстремума или на границе множества.
Пример
3. Найти
наибольшее и наименьшее значения функции
в области
.
Решение. Изобразим данную область на координатной плоскости:
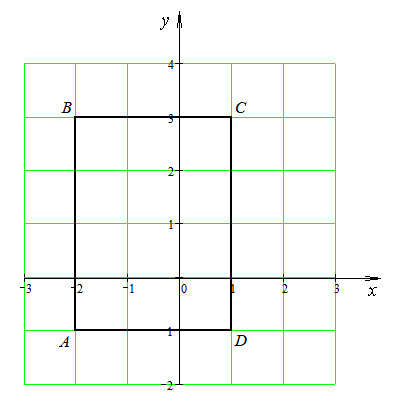
1) Находим критические точки функции:
-
критическая точка.
значение
функции z
в этой точке вычислять не нужно.
2) Находим значения функции на границах области:
х
= -2:
-
получили функцию одной переменной.
Находим её производную, приравниваем
её к нулю, чтобы найти критические точки:
.
Находим значение функции z
в точке
.
х
= 1:
.
Находим значение функции z
в точке
.
y
= -1:
точка
значение функции z
в этой точке вычислять не нужно.
y
= 3:
точка
значение функции z
в этой точке вычислять не нужно.
3) Находим значения функции в угловых точках:
.
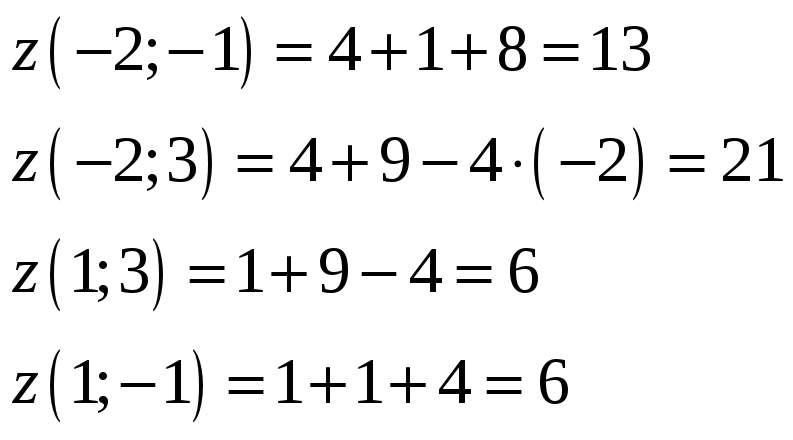
Из найденных значений 12, -3, 13, 21, 6, выбираем наибольшее и наименьшее.
Ответ: М = 21, m = -3.
Условный экстремум
Пусть
рассматривается функция
,
аргументы которой удовлетворяют условию
,
называемому уравнением
связи.
Точка
называется точкой условного
максимума
(минимума),
если существует такая окрестность этой
точки, что для всех точек
из этой окрестности, удовлетворяющих
условию
,
выполняется неравенство:
.
Если
выразить у
через х
из уравнения связи
и подставить в функцию
,
то полученная функция
будет являться функцией одной переменной,
для которой можно найти её экстремумы,
они будут являться условными экстремумами
функции
.
Пример
4. Найти точки
максимума и минимума функции
при условии
.
Решение.
Выразим из уравнения связи переменную
у:
.
Находим
экстремумы:
-
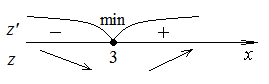
точка условного минимума.
В данном примере уравнение связи являлось линейным, поэтому его легко можно решить относительно одной из переменных. Для случаев, когда уравнение связи имеет более сложный вид, применяется метод множителей Лагранжа.
Метод множителей Лагранжа
Рассмотрим
функцию трёх переменных
.
Эта функция называется функцией
Лагранжа, λ
– множителем
Лагранжа.
Теорема.
Если точка
является точкой условного экстремума
функции
при условии
,
то существует значение
такое, что точка
является точкой экстремума функции
.
Таким
образом, для нахождения условного
экстремума функции
при условии
требуется найти решение системы уравнений
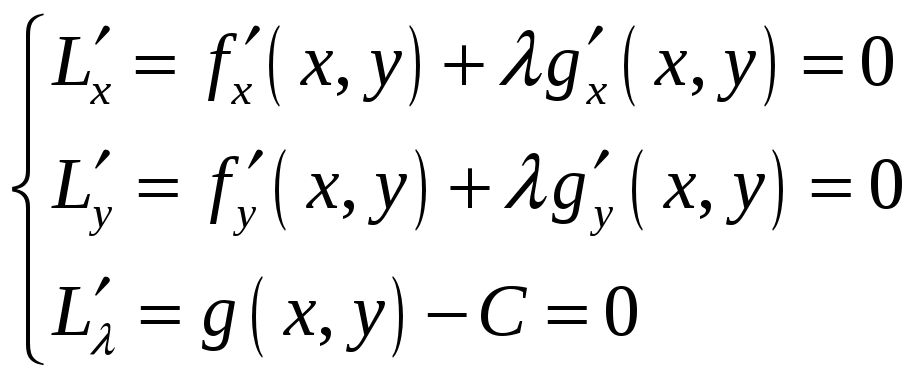
Далее,
для каждой из точек
находят определитель
.
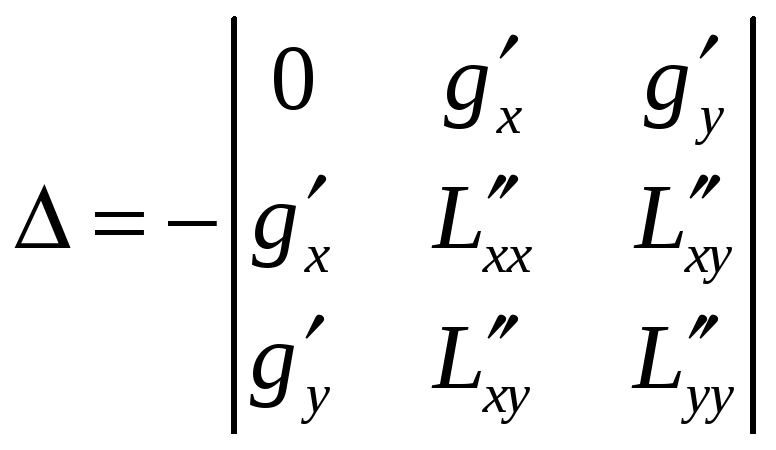Если
,
то точка
является
точкой условного
минимума,
если
- условного
максимума.
Геометрический
смысл условий Лагранжа:
.
В точке условного экстремума градиенты
функций
и
коллинеарны.
Пример
5. Найти
условные экстремумы функции
при
.
Решение.
Запишем функцию Лагранжа:
.
Находим частые производные функции Лагранжа и решаем систему уравнений:
.
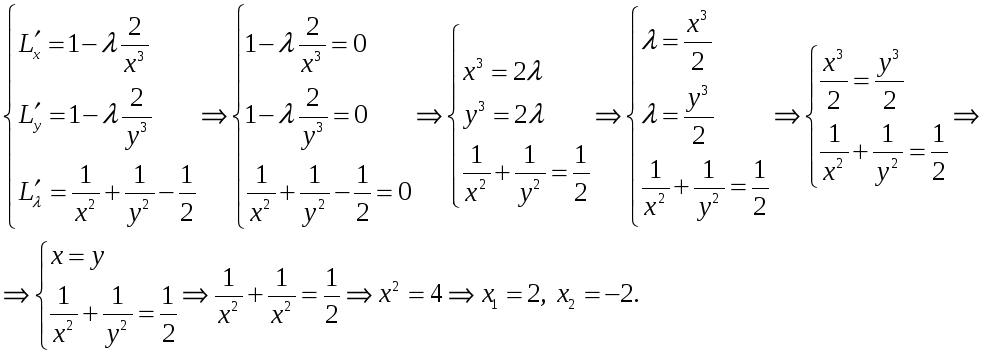
Получили
две точки
и
.
Для каждой из них найдём определитель
Δ.
.
Для
точки
:
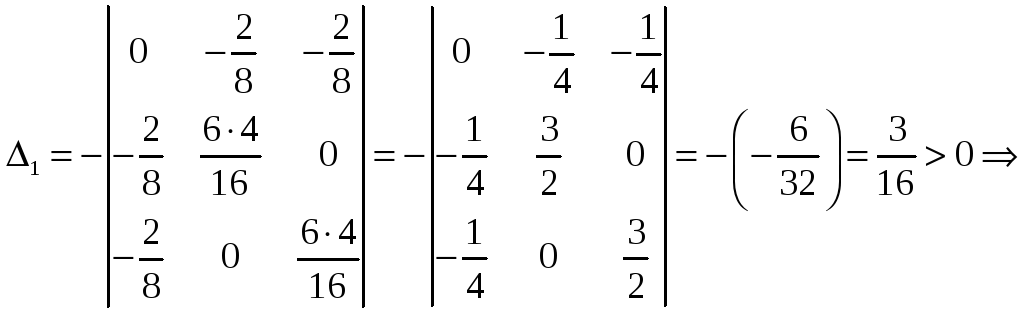в
точке
-
условный
минимум;
.
Для
точки
:
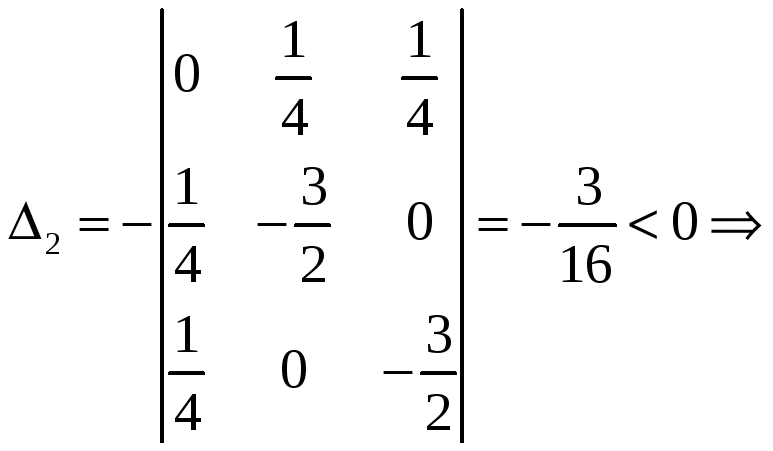в
точке
-
условный максимум;
.
Задания для самостоятельного решения
Исследовать на экстремум функции:
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
Исследовать функции на условный экстремум:
13.
14.
15.
16.
17.
18.
19.
20.
21.
22.
23.
24.
25.
26.
27.
