
- •7. Определённый интеграл Понятие определённого интеграла
- •Интегрирование по частям в определённом интеграле
- •Вычисление площадей плоских фигур
- •Вычисление объёмов тел вращения
- •Несобственные интегралы
- •8. Числовые ряды
- •Свойства сходящихся рядов
- •Необходимый признак сходимости
- •Ряды с положительными членами. Признаки сходимости
- •Знакочередующиеся числовые ряды
- •Знакопеременные ряды
- •9. Степенные ряды
- •Область сходимости степенного ряда
- •Свойства степенных рядов
- •Ряд Маклорена
- •Применение рядов в приближённых вычислениях
- •10. Функции нескольких переменных
- •Предел и непрерывность
- •Частные производные
- •Дифференциал функции
- •Градиент
- •Производная по направлению
- •Частные производные высших порядков
- •11. Исследование функции нескольких переменных Экстремум функции нескольких переменных
- •Наибольшее и наименьшее значения функции двух переменных
- •Условный экстремум
- •Метод множителей Лагранжа
- •12. Общие понятия теории дифференциальных уравнений. Дифференциальные уравнения 1-го порядка
- •Уравнения с разделяющимися переменными
- •Однородные уравнения
- •Линейные уравнения
- •Уравнения в полных дифференциалах
- •13. Дифференциальные уравнения высших порядков Основные понятия и определения
- •Уравнения, допускающие понижение порядка
- •Линейные дифференциальные уравнения второго порядка
- •Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами
- •Линейные неоднородные дифференциальные уравнения второго порядка с постоянными коэффициентами
- •Метод вариации произвольных постоянных
Вычисление объёмов тел вращения
Кривая
![]() вращается вокруг оси Ох,
при этом образуется некое тело вращения.
Всякое сечение тела вращения – круг
радиуса
вращается вокруг оси Ох,
при этом образуется некое тело вращения.
Всякое сечение тела вращения – круг
радиуса
![]() в сечении х.
Объём тела вращения вычисляется по
формуле
в сечении х.
Объём тела вращения вычисляется по
формуле
![]() .
.
Пример
6. В плоскости
Оху
задана функция
![]() на отрезке
на отрезке
![]() .
Найти объём тела, полученного в результате
вращения
.
Найти объём тела, полученного в результате
вращения
![]() вокруг оси Ох.
вокруг оси Ох.
Решение.


Несобственные интегралы
В
соответствии с определением интеграла
по Риману, функция
![]() должна быть ограничена на
должна быть ограничена на
![]() ,
а сам отрезок
,
а сам отрезок
![]() конечен. Однако в ряде технических задач
требуется вычислить определённый
интеграл, промежуток интегрирования
которого является бесконечным, т.е. один
или оба предела интегрирования равны
конечен. Однако в ряде технических задач
требуется вычислить определённый
интеграл, промежуток интегрирования
которого является бесконечным, т.е. один
или оба предела интегрирования равны
![]() .
Функция
.
Функция
![]() может иметь внутри промежутка
интегрирования точки разрыва второго
рода, т.е.
может иметь внутри промежутка
интегрирования точки разрыва второго
рода, т.е.
![]() неограниченна. При этом такие интегралы
могут существовать, т.е. принимать
конечные значения.
неограниченна. При этом такие интегралы
могут существовать, т.е. принимать
конечные значения.
Определённый
интеграл
![]() называется несобственным
интегралом,
если выполняется, по крайней мере одно
из следующих условий:
называется несобственным
интегралом,
если выполняется, по крайней мере одно
из следующих условий:
-
Предел a или b (или оба предела) являются бесконечными;
-
Функция f (x) имеет одну или несколько точек разрыва внутри [a,b].
Несобственные интегралы I рода – интегралы с бесконечными пределами интегрирования. Их вычисление осуществляется следующим образом:
1.
![]()
2.
![]()
3.
![]()
Если
предел существует, то несобственный
интеграл сходится и равен этому пределу.
Если предел равен
![]() ,
то интеграл расходится, то есть не
существует.
,
то интеграл расходится, то есть не
существует.
Пример
7. Вычислить
интеграл
![]()
Решение.

![]()
Несобственные интегралы II рода.
Пусть
функция
![]() непрерывна на
непрерывна на
![]() ,
исключая точку
,
исключая точку
![]() ,
в которой
,
в которой
![]() имеет разрыв второго рода
имеет разрыв второго рода
![]() .
Интеграл от такой функции называется
несобственным
интегралом
II
рода.
Вычисляется он следующим образом:
возьмём на
.
Интеграл от такой функции называется
несобственным
интегралом
II
рода.
Вычисляется он следующим образом:
возьмём на
![]() окрестность точки с
радиуса ε.
окрестность точки с
радиуса ε.

Тогда
вне этой окрестности
![]() интегрируема. Вычисляется предел при
интегрируема. Вычисляется предел при
![]() .
.
1.
Если точка разрыва
![]() :
:
![]()
2.
Если точка разрыва
![]() :
:
![]()
3.
Если точка разрыва
![]() :
:
![]()
Если данный предел существует, то несобственный интеграл сходит и равен этому пределу.
Пример
8. Вычислить
интеграл
 .
.
Решение.
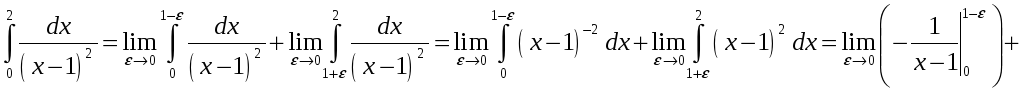

![]() несобственный
интеграл расходится.
несобственный
интеграл расходится.
Задания для самостоятельного решения
Вычислить интегралы:
1.
![]() 2.
2.
![]() 3.
3.
![]() 4.
4.
![]() 5.
5.
![]()
6.
![]() 7.
7.
 8.
8.
![]() 9.
9.
 10.
10.
![]()
11.
 12.
12.
![]() 13.
13.
 14.
14.
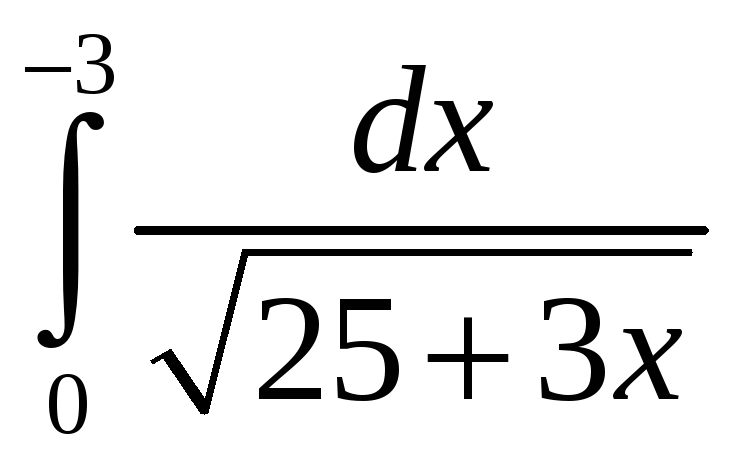
15.
 16.
16.
![]() 17.
17.
![]() 18.
18.

19.
![]() 20.
20.
 21.
21.
 22.
22.
![]()
23.
 24.
24.
 25.
25.
 26.
26.
![]()
27.
![]() 28.
28.
![]() 29.
29.
![]() 30.
30.
![]()
Вычислить площади фигур, ограниченных линиями:
31.
![]() 32.
32.
![]() 33.
33.
![]()
34.
![]() 35.
35.
![]() 36.
36.
![]()
37.
![]() 38.
38.
![]() 39.
39.
![]()
40.
![]() 41.
41.
![]() 42.
42.
![]()
Вычислить объём тела, образованного вращением вокруг оси Ох фигуры, ограниченной линиями:
43.
![]() 44.
44.
![]()
45.
![]() 46.
46.
![]()
47.
![]() 48.
48.
![]()
49.
![]() 50.
50.
![]() 51.
51.
![]()
Вычислить несобственный интеграл или установить его расходимость:
52.
![]() 53.
53.
![]() 54.
54.
![]() 55.
55.
![]() 56.
56.
![]()
57.
![]() 58.
58.
![]() 59.
59.
![]() 60.
60.
![]() 61.
61.
![]()
62.
![]() 63.
63.
 64.
64.
![]() 65.
65.
![]()
66.
 67.
67.
 68.
68.
![]() 69.
69.
![]()
8. Числовые ряды
Числовым
рядом
называется бесконечная последовательность
чисел
![]() .
Числа
.
Числа
![]() называются членами ряда, а член
называются членами ряда, а член
![]() - общим членом ряда.
- общим членом ряда.
Например,
общим членом ряда
 является
является
 .
.
Пример
1. Найти в
простейшей форме общий член ряда
![]()
![]() .
.
Рассмотрим суммы конечного числа членов ряда:
![]() .
.
Сумма
n
первых членов ряда
![]() называется n-ной
частичной
суммой ряда.
называется n-ной
частичной
суммой ряда.
Ряд
называется сходящимся,
если существует конечный предел
последовательности его частичных сумм,
то есть
![]() .
.
Число
S
называется суммой
ряда:
![]() .
.
Если конечного предела последовательности частичных сумм не существует, то ряд называется расходящимся.
