
- •7. Определённый интеграл Понятие определённого интеграла
- •Интегрирование по частям в определённом интеграле
- •Вычисление площадей плоских фигур
- •Вычисление объёмов тел вращения
- •Несобственные интегралы
- •8. Числовые ряды
- •Свойства сходящихся рядов
- •Необходимый признак сходимости
- •Ряды с положительными членами. Признаки сходимости
- •Знакочередующиеся числовые ряды
- •Знакопеременные ряды
- •9. Степенные ряды
- •Область сходимости степенного ряда
- •Свойства степенных рядов
- •Ряд Маклорена
- •Применение рядов в приближённых вычислениях
- •10. Функции нескольких переменных
- •Предел и непрерывность
- •Частные производные
- •Дифференциал функции
- •Градиент
- •Производная по направлению
- •Частные производные высших порядков
- •11. Исследование функции нескольких переменных Экстремум функции нескольких переменных
- •Наибольшее и наименьшее значения функции двух переменных
- •Условный экстремум
- •Метод множителей Лагранжа
- •12. Общие понятия теории дифференциальных уравнений. Дифференциальные уравнения 1-го порядка
- •Уравнения с разделяющимися переменными
- •Однородные уравнения
- •Линейные уравнения
- •Уравнения в полных дифференциалах
- •13. Дифференциальные уравнения высших порядков Основные понятия и определения
- •Уравнения, допускающие понижение порядка
- •Линейные дифференциальные уравнения второго порядка
- •Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами
- •Линейные неоднородные дифференциальные уравнения второго порядка с постоянными коэффициентами
- •Метод вариации произвольных постоянных
Знакочередующиеся числовые ряды
Знакочередующийся
ряд – ряд,
в котором члены попеременно то
положительны, то отрицательны:
![]() ,
где
,
где
![]() .
.
Признак Лейбница
Если
члены знакочередующегося ряда убывают
по абсолютной величине (по модулю)
![]() и предел его общего члена при
и предел его общего члена при
![]() равен нулю, т.е.
равен нулю, т.е.
![]() ,
то ряд сходится, а его сумма не превосходит
первого члена ряда
,
то ряд сходится, а его сумма не превосходит
первого члена ряда
![]() .
.
Пример
11. Исследовать
сходимость ряда
![]() .
.
Решение.
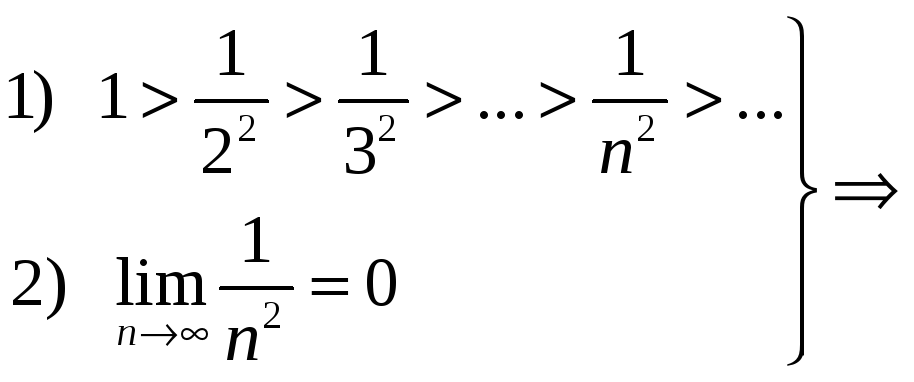 ряд
сходится по признаку Лейбница.
ряд
сходится по признаку Лейбница.
Знакопеременные ряды
Пусть
![]() - знакопеременный
ряд, в котором
любой член
- знакопеременный
ряд, в котором
любой член
![]() может быть как положительным, так и
отрицательным.
может быть как положительным, так и
отрицательным.
Достаточный признак сходимости знакопеременного ряда
Если
ряд, составленный из модулей членов
данного ряда
![]() сходится, то сходится и данный ряд.
сходится, то сходится и данный ряд.
Заметим, что обратное утверждение неверно.
Ряд называется абсолютно сходящимся, если сходится как сам ряд, так и ряд, составленный из абсолютных величин его членов.
Ряд называется условно сходящимся, сам ряд сходится, а ряд, составленный из абсолютных величин его членов, расходится.
Пример
12. Исследовать
сходимость ряда
![]() .
.
Решение.
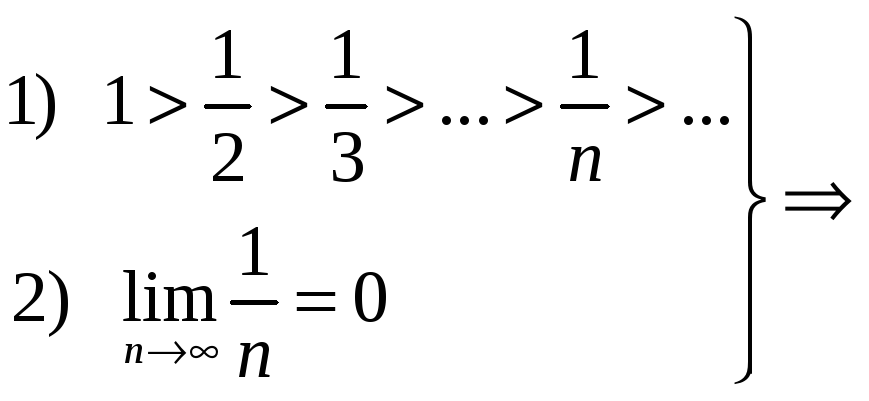 ряд
сходится по признаку Лейбница.
ряд
сходится по признаку Лейбница.
3)
Ряд, составленный из модулей, имеет вид
![]() .
Это гармонический ряд, следовательно,
он расходится.
.
Это гармонический ряд, следовательно,
он расходится.
Ответ:
ряд
![]() сходится условно.
сходится условно.
Пример
13. Исследовать
сходимость ряда
![]() .
.
Решение.
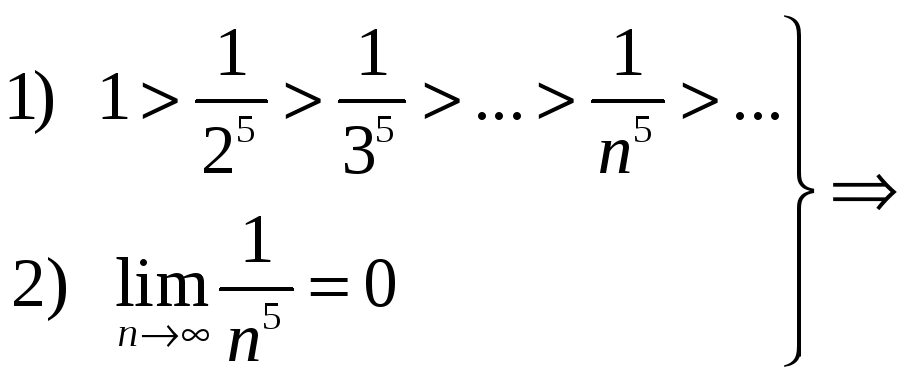 ряд
сходится по признаку Лейбница.
ряд
сходится по признаку Лейбница.
3)
Ряд, составленный из модулей, имеет вид
![]() .
Это обобщенный гармонический ряд,
.
Это обобщенный гармонический ряд,
![]() ,
следовательно, он сходится.
,
следовательно, он сходится.
Ответ:
ряд
![]() сходится абсолютно.
сходится абсолютно.
Пример
14. Исследовать
сходимость ряда
![]() .
.
Решение.
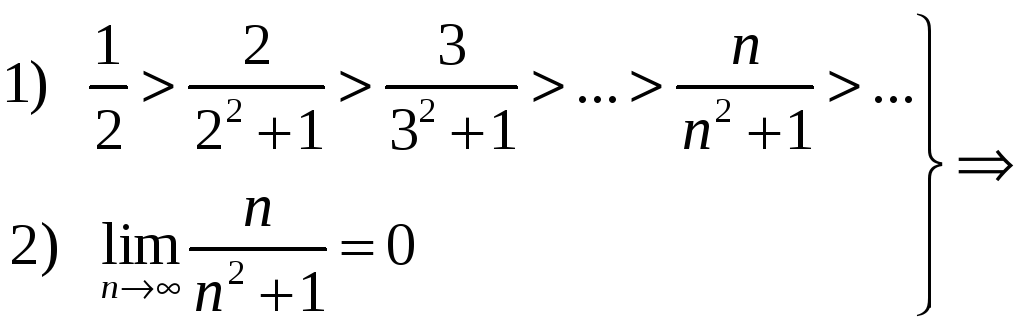 ряд
сходится по признаку Лейбница.
ряд
сходится по признаку Лейбница.
3)
Ряд, составленный из модулей, имеет вид
![]() .
Исследуем его сходимость, для этого
применим предельный признак сравнения.
Сравним с расходящимся гармоническим
рядом
.
Исследуем его сходимость, для этого
применим предельный признак сравнения.
Сравним с расходящимся гармоническим
рядом
![]() .
Найдём предел
.
Найдём предел
![]() ряд
ряд
![]() расходится.
расходится.
Ответ:
ряд
![]() сходится условно.
сходится условно.
Задания для самостоятельного решения
Исследовать сходимость ряда:
1.
![]() 2.
2.
![]() 3.
3.
![]() 4.
4.
![]()
5.
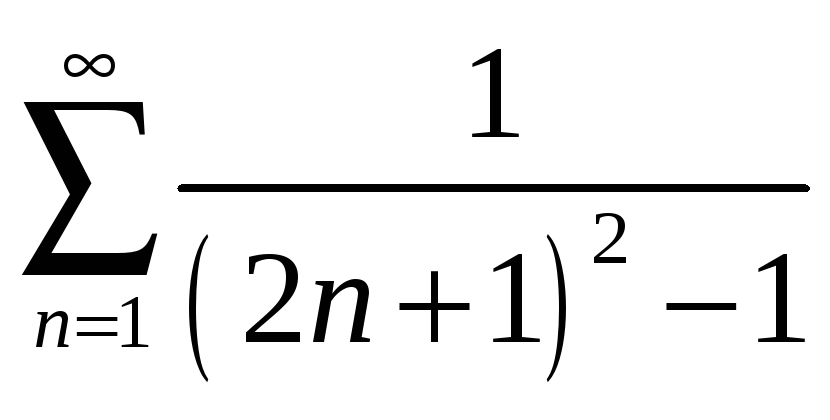 6.
6.
![]() 7.
7.
![]() 8.
8.
![]()
9.
![]() 10.
10.
![]() 11.
11.
![]() 12.
12.
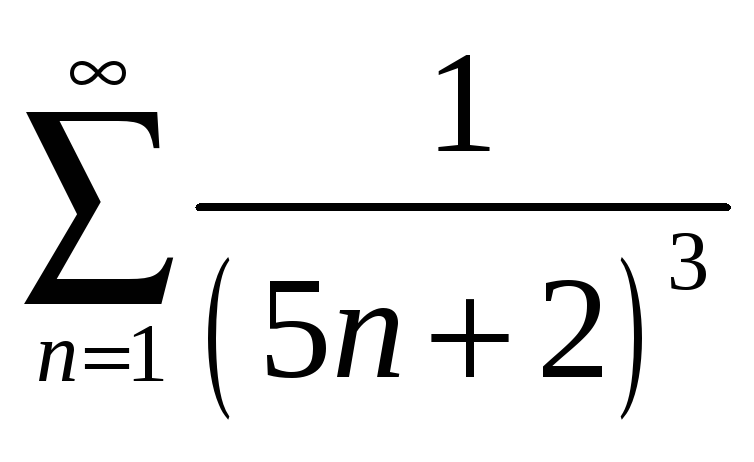
13.
![]() 14.
14.
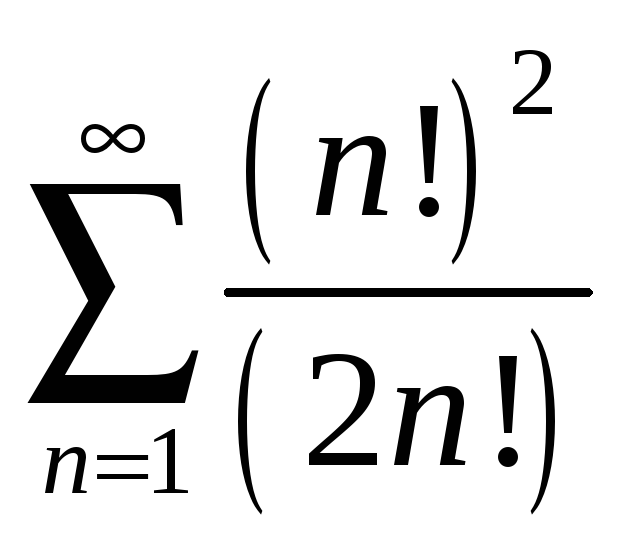 15.
15.
![]() 16.
16.
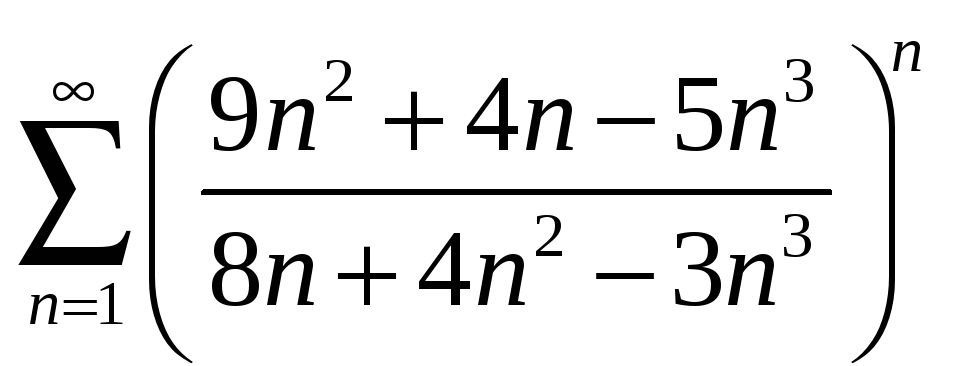
17.
![]() 18.
18.
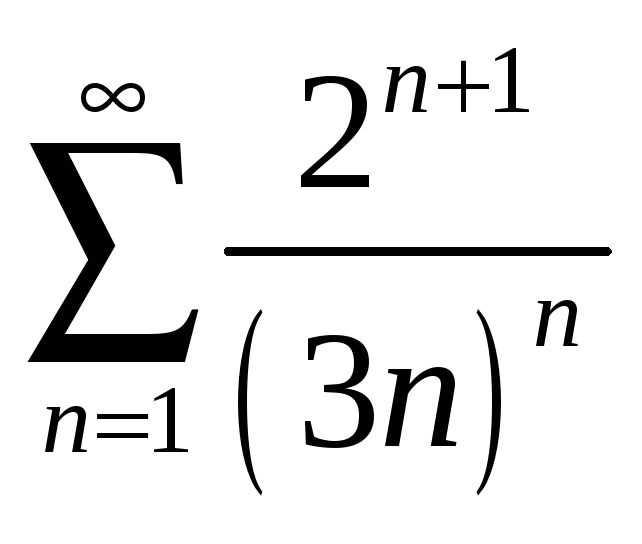 19.
19.
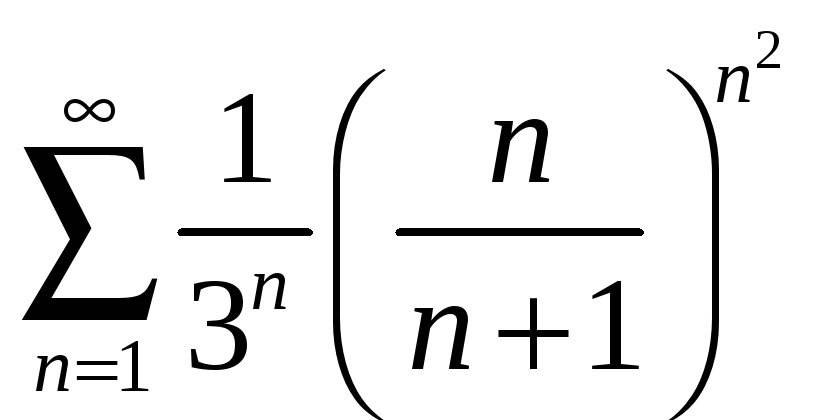 20.
20.
![]()
21.
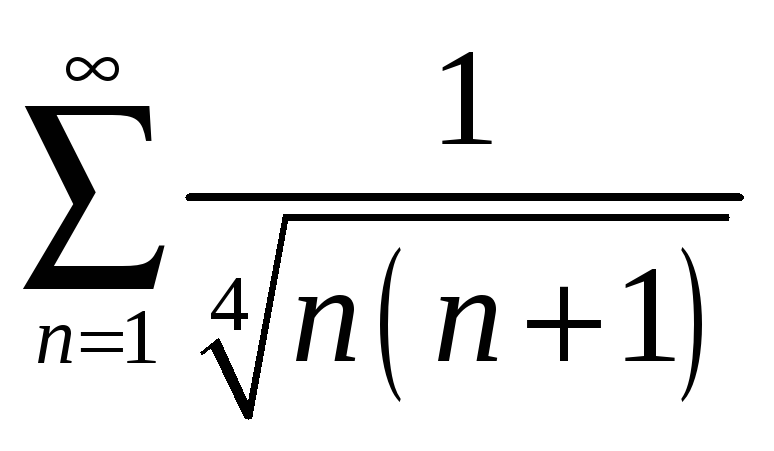 22.
22.
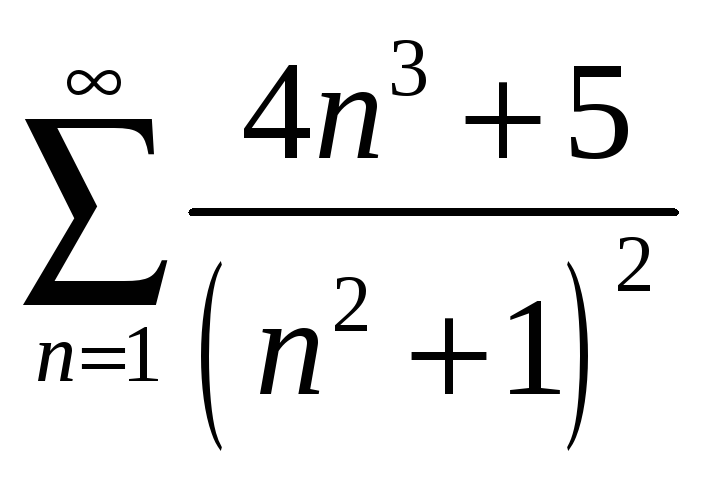 23.
23.
![]() 24.
24.
![]()
25.
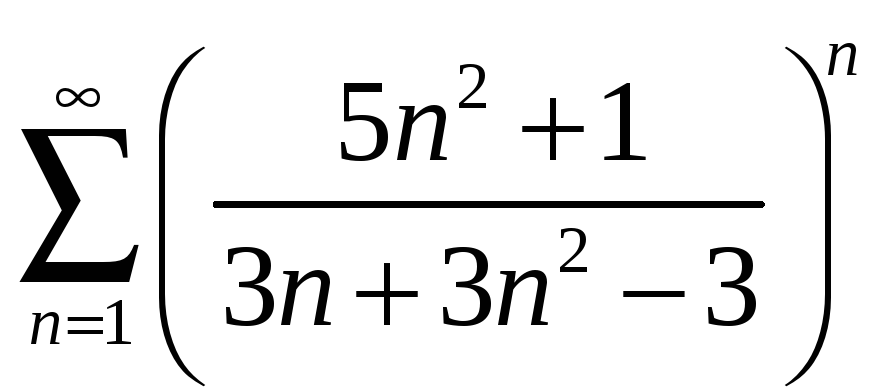 26.
26.
![]() 27.
27.
![]() 28.
28.
![]()
30.
![]() 31.
31.
![]() 32.
32.
![]() 33.
33.
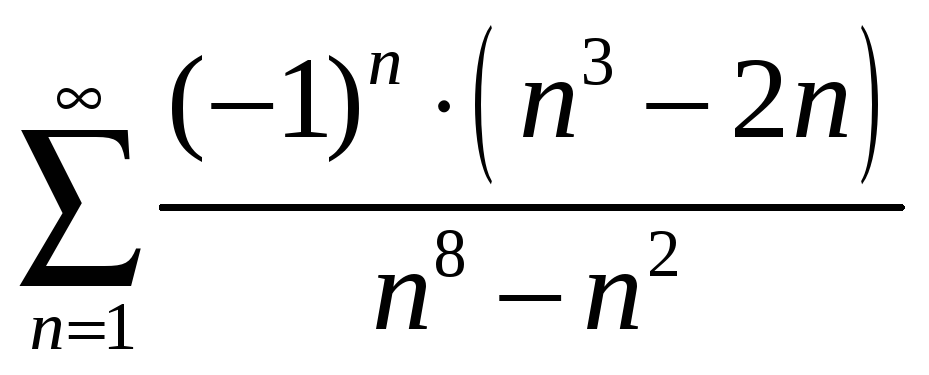
34.
![]() 35.
35.
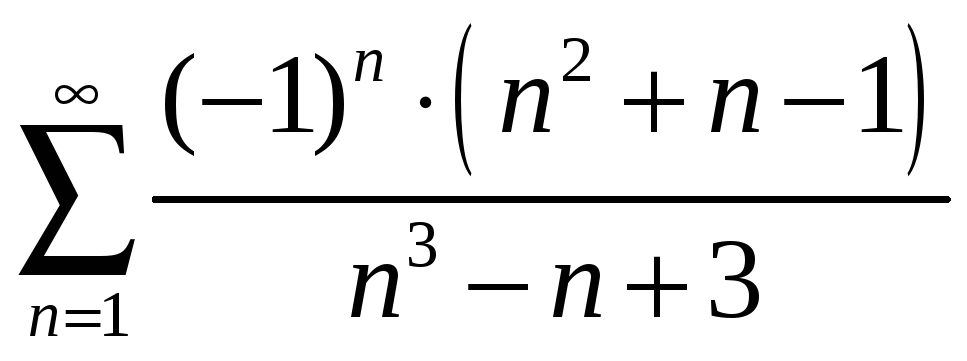 36.
36.
![]() 37.
37.
![]()
38.
![]() 39.
39.
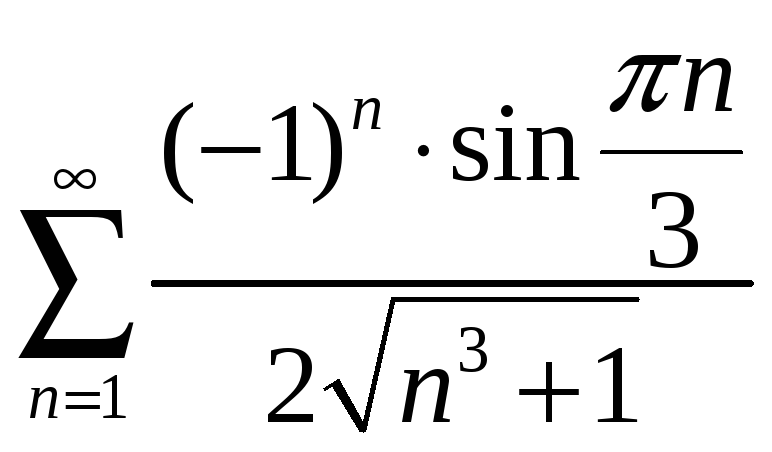 40.
40.
![]()
9. Степенные ряды
Ряды,
членами которых являются степенные
функции, называются степенными
![]() .
Числа
.
Числа
![]() называются коэффициентами
степенного ряда.
называются коэффициентами
степенного ряда.
Область сходимости степенного ряда
Совокупность тех значений х, при которых степенной ряд сходится, называется областью сходимости степенного ряда.
Пример
1. Найти
область сходимости степенного ряда
![]() .
.
Решение.
Ряд можно рассматривать как геометрический
ряд со знаменателем
![]() ,
который сходится при
,
который сходится при
![]() .
Отсюда
.
Отсюда
![]() ,
т.е. областью сходимости является
интервал
,
т.е. областью сходимости является
интервал
![]() .
.
Структура области сходимости степенного ряда устанавливается с помощью теоремы Абеля.
1)
Если степенной ряд сходится при значении
![]() (отличном от нуля), то он сходится, и
притом абсолютно, при всех значениях
х,
таких, что
(отличном от нуля), то он сходится, и
притом абсолютно, при всех значениях
х,
таких, что
![]() .
.
2)
Если степенной ряд расходится при
![]() ,
то он расходится при всех значениях х,
таких, что
,
то он расходится при всех значениях х,
таких, что
![]() .
.
Из
теоремы следует, что существует такое
число
![]() ,
что при
,
что при
![]() ряд сходится, а при
ряд сходится, а при
![]() - расходится. Число R
называется радиусом
сходимости.
- расходится. Число R
называется радиусом
сходимости.
Интервал
![]() - интервалом
сходимости степенного
ряда.
- интервалом
сходимости степенного
ряда.
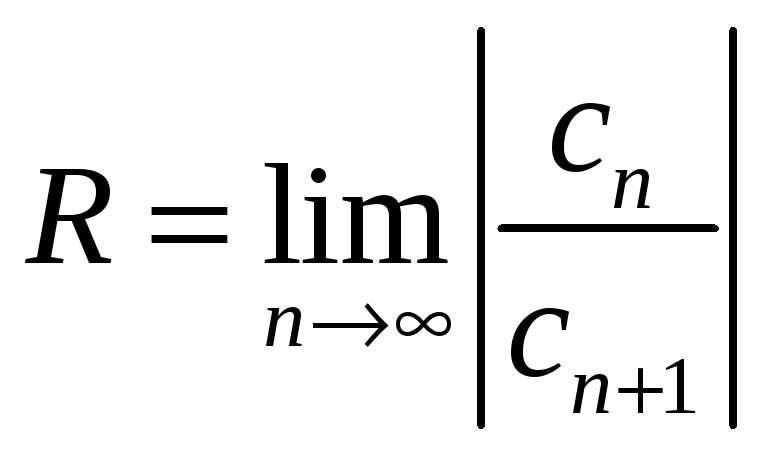
Для нахождения области сходимости, сначала находят интервал сходимости, затем проверяют сходимость ряда на концах интервала.
