
- •7. Определённый интеграл Понятие определённого интеграла
- •Интегрирование по частям в определённом интеграле
- •Вычисление площадей плоских фигур
- •Вычисление объёмов тел вращения
- •Несобственные интегралы
- •8. Числовые ряды
- •Свойства сходящихся рядов
- •Необходимый признак сходимости
- •Ряды с положительными членами. Признаки сходимости
- •Знакочередующиеся числовые ряды
- •Знакопеременные ряды
- •9. Степенные ряды
- •Область сходимости степенного ряда
- •Свойства степенных рядов
- •Ряд Маклорена
- •Применение рядов в приближённых вычислениях
- •10. Функции нескольких переменных
- •Предел и непрерывность
- •Частные производные
- •Дифференциал функции
- •Градиент
- •Производная по направлению
- •Частные производные высших порядков
- •11. Исследование функции нескольких переменных Экстремум функции нескольких переменных
- •Наибольшее и наименьшее значения функции двух переменных
- •Условный экстремум
- •Метод множителей Лагранжа
- •12. Общие понятия теории дифференциальных уравнений. Дифференциальные уравнения 1-го порядка
- •Уравнения с разделяющимися переменными
- •Однородные уравнения
- •Линейные уравнения
- •Уравнения в полных дифференциалах
- •13. Дифференциальные уравнения высших порядков Основные понятия и определения
- •Уравнения, допускающие понижение порядка
- •Линейные дифференциальные уравнения второго порядка
- •Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами
- •Линейные неоднородные дифференциальные уравнения второго порядка с постоянными коэффициентами
- •Метод вариации произвольных постоянных
Дифференциал функции
Дифференциалом
функции
называется сумма произведений частных
производных этой функции на приращения
соответствующих переменных, т.е.
![]() .
.
Градиент
Градиентом
![]() функции z =
f(x,
y)
называется вектор с координатами
функции z =
f(x,
y)
называется вектор с координатами
![]() .
Градиент функции
.
Градиент функции
![]() в данной точке характеризует направление
максимальной скорости изменения функции
в этой точке.
в данной точке характеризует направление
максимальной скорости изменения функции
в этой точке.
Теорема.
Пусть задана дифференцируемая функция
z = f(x,
y)
и пусть в точке
![]() ,
величина градиента отлична от нуля.
Тогда градиент перпендикулярен линии
уровня, проходящей через данную точку.
,
величина градиента отлична от нуля.
Тогда градиент перпендикулярен линии
уровня, проходящей через данную точку.
Таким образом, линии уровня можно построить следующим образом.
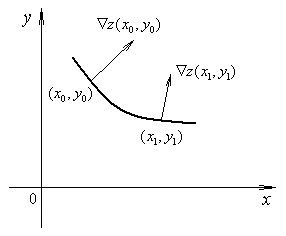
Предположим,
мы начинаем с точки
![]() .
Построим градиент в этой точке. Задаем
направление, перпендикулярное градиенту.
Оно позволяет построить малую часть
линии уровня. Далее рассмотрим близкую
точку
.
Построим градиент в этой точке. Задаем
направление, перпендикулярное градиенту.
Оно позволяет построить малую часть
линии уровня. Далее рассмотрим близкую
точку
![]() и построим градиент в ней. Продолжая
этот процесс, можно (с определенной
погрешностью) построить линии уровня.
и построим градиент в ней. Продолжая
этот процесс, можно (с определенной
погрешностью) построить линии уровня.
Пример
6. Найти
градиент функции
![]() в точке М(1; 1).
в точке М(1; 1).
Решение. Находим частные производные функции z:
![]() .
.
Подставляем
значения х
= 1 и y
= 1(координаты
точки М) в частные производные:
![]() .
.
Ответ:
![]() .
.
Производная по направлению
Производной
![]() по направлению
вектора
по направлению
вектора
![]() функции двух переменных
функции двух переменных
![]() называется
предел отношения приращения функции в
этом направлении к величине перемещения
называется
предел отношения приращения функции в
этом направлении к величине перемещения
![]() при
при
![]() :
:
![]()
![]() характеризует скорость изменения
функции в направлении
характеризует скорость изменения
функции в направлении
![]() .
.
![]()
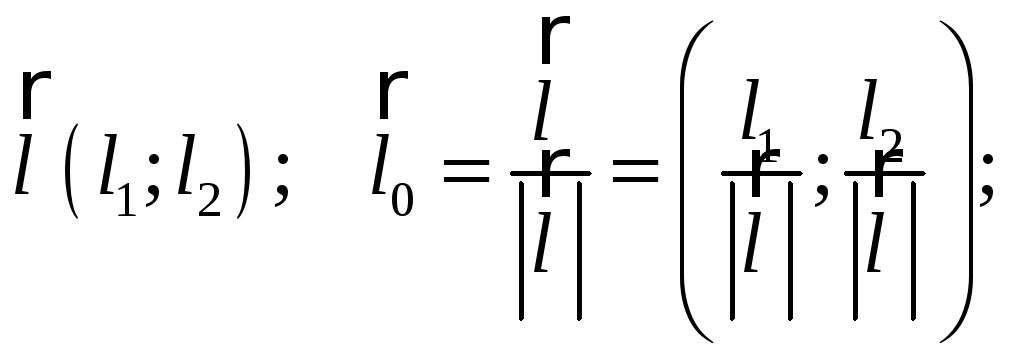
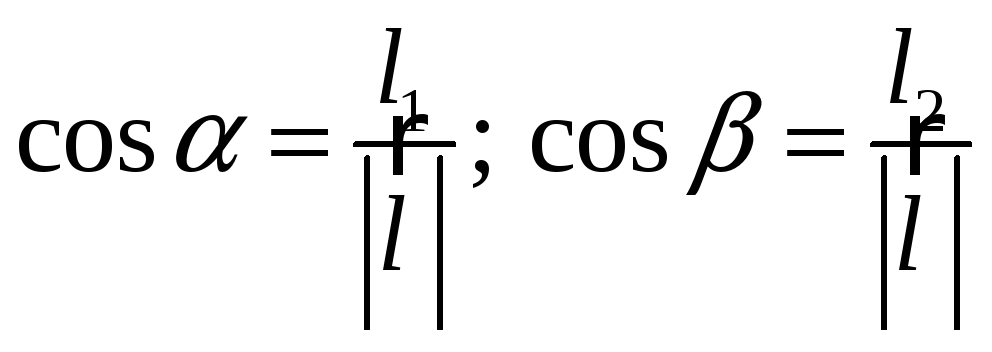 - направляющие
косинусы.
- направляющие
косинусы.
Пример
7. Вычислить
производную функции
![]() в точке М(1; 1) по направлению вектора
в точке М(1; 1) по направлению вектора
![]() .
.
Решение.
1)
![]() .
.
![]() .
.
2)
![]()
![]()
3)
![]() .
.
Частные производные высших порядков
Если
частные производные
![]() и
и
![]() сами являются дифференцируемыми
функциями, то можно найти так же и их
частные производные, которые называются
частными
производными второго порядка.
сами являются дифференцируемыми
функциями, то можно найти так же и их
частные производные, которые называются
частными
производными второго порядка.
Частные
производные от
![]() :
:
![]() и
и
![]() .
.
Частные
производные от
![]() :
:
![]() и
и
![]() .
.
Если
частные производные второго порядка
функции z
непрерывны в точке
![]() ,
то в этой точке
,
то в этой точке
![]() .
.
Пример
8. Найти
частные производные второго порядка
для функции
![]() .
.
Решение.
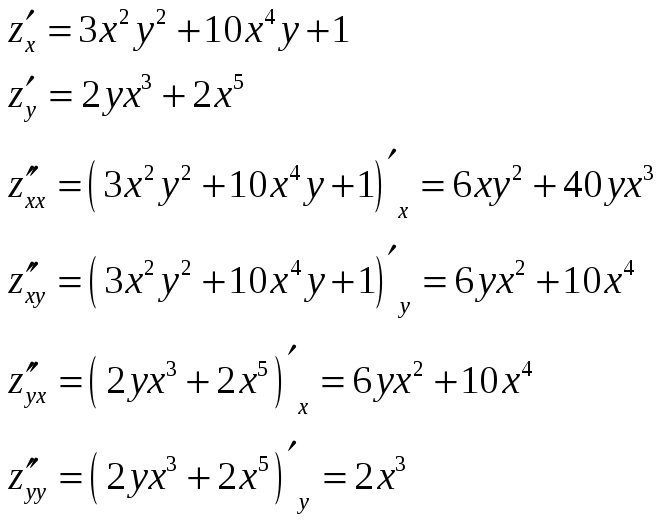
Задания для самостоятельного решения
Найти частные производные функций:
1.
![]() 2.
2.
![]() 3.
3.
![]() 4.
4.
![]()
5.
![]() 6.
6.
![]() 7.
7.
![]() 8.
8.
![]()
9.
![]() 10.
10.
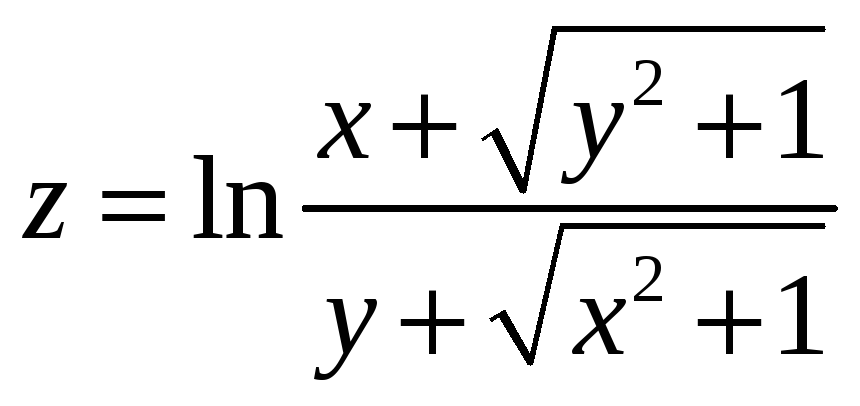 11.
11.
![]() 12.
12.
![]()
Найти градиент функции в точке.
13.
![]() 14.
14.
![]() 15.
15.
![]()
16.
![]() 17.
17.
![]() 18.
18.
![]()
19.
![]() 20.
20.
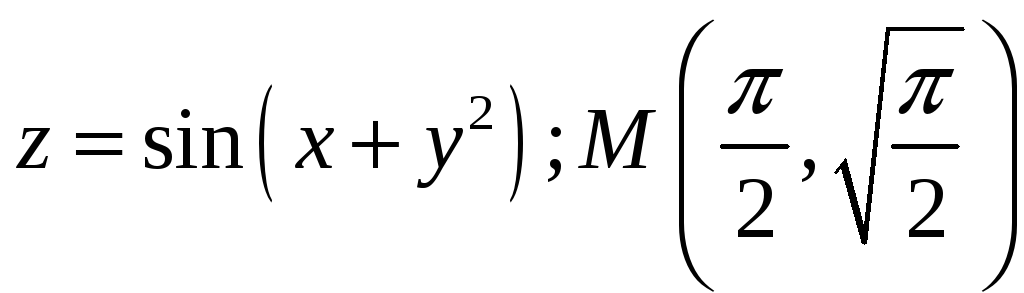 21.
21.
![]()
22.
Найти производную функции
![]() в
точке M (–9; –1) в направлении вектора
в
точке M (–9; –1) в направлении вектора
![]() .
.
23.
Найти производную функции
![]() в точке М (0; 0) в направлении вектора
в точке М (0; 0) в направлении вектора
![]() .
.
24.
Найти
производную функции
![]() в точке М (-2; 3) в направлении вектора
в точке М (-2; 3) в направлении вектора
![]() .
.
25.
Найти производную функции
![]() в точке М (1; 1) в направлении вектора
в точке М (1; 1) в направлении вектора
![]() .
.
26.
Найти производную функции
![]() в точке А (1; 2) по направлению вектора
в точке А (1; 2) по направлению вектора
![]() ;
В (3; 0).
;
В (3; 0).
27.
Найти производную функции
![]() в точке М(1; 1) в направлении вектора
в точке М(1; 1) в направлении вектора
![]() ,
составляющем угол =60о
с положительным направлением оси Ох.
,
составляющем угол =60о
с положительным направлением оси Ох.
28.
Найти производную функции
![]() в точке М (3; 4) в направлении градиента
функции z.
в точке М (3; 4) в направлении градиента
функции z.
Найти частные производные второго порядка функций:
29.
![]() 30.
30.
![]() 31.
31.
![]()
32.
![]() 33.
33.
![]() 34.
34.
![]() 35.
35.
![]()
36.
![]() 37.
37.
![]() 38.
38.
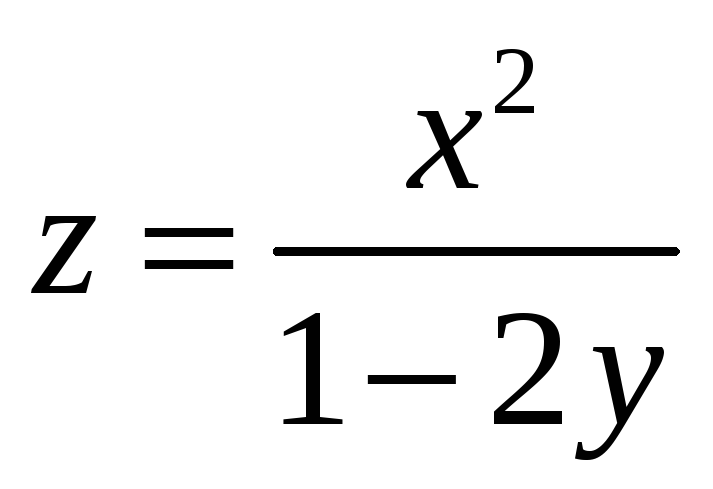 39.
39.
![]()
11. Исследование функции нескольких переменных Экстремум функции нескольких переменных
Точка
![]() называется точкой максимума
(минимума)
функции
называется точкой максимума
(минимума)
функции
z
= f(x,
y),
если существует окрестность точки М,
такая, что для всех точек (х,
у)
из этой окрестности выполняется
неравенство
![]()
Сформулируем необходимое условие экстремума – многомерный аналог теоремы Ферма.
Теорема.
Пусть точка
![]() есть точка экстремума дифференцируемой
функции z =
f(x,
y).
Тогда частные производные
есть точка экстремума дифференцируемой
функции z =
f(x,
y).
Тогда частные производные
![]() и
и
![]() в этой точке равны нулю.
в этой точке равны нулю.
Точки,
в которых выполнены необходимые условия
экстремума функции z
= f(x,
y),
т.е. частные производные
![]() и
и
![]() равны нулю, называются критическими
или стационарными.
равны нулю, называются критическими
или стационарными.
Теорема
(достаточное условие экстремума функции
двух переменных).
Пусть функция z
= f(x,
y):
а) определена в некоторой окрестности
критической точки
![]() ,
в которой
,
в которой
![]() и
и
![]() ;
б) имеет в этой точке непрерывные частные
производные второго порядка:
;
б) имеет в этой точке непрерывные частные
производные второго порядка:
![]() .
.
![]() .
Тогда, если
.
Тогда, если
![]() ,
то в точке
,
то в точке
![]() функция z =
f(x,
y)
имеет экстремум, причем если А
< 0 – максимум, если А
> 0 – минимум. В случае
функция z =
f(x,
y)
имеет экстремум, причем если А
< 0 – максимум, если А
> 0 – минимум. В случае
![]() ,
функция z =
f(x,
y)
экстремума не имеет. Если
,
функция z =
f(x,
y)
экстремума не имеет. Если
![]() ,
то вопрос о наличии экстремума остается
открытым.
,
то вопрос о наличии экстремума остается
открытым.
Исследование функции двух переменных на экстремум рекомендуется проводить по следующей схеме:
-
Найти частные производные функции
 и
и
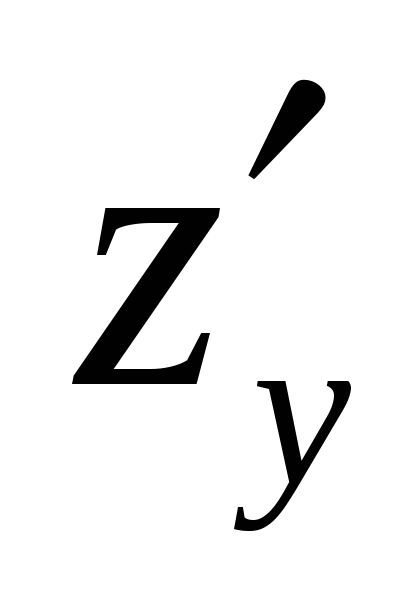 .
. -
Решить систему уравнений
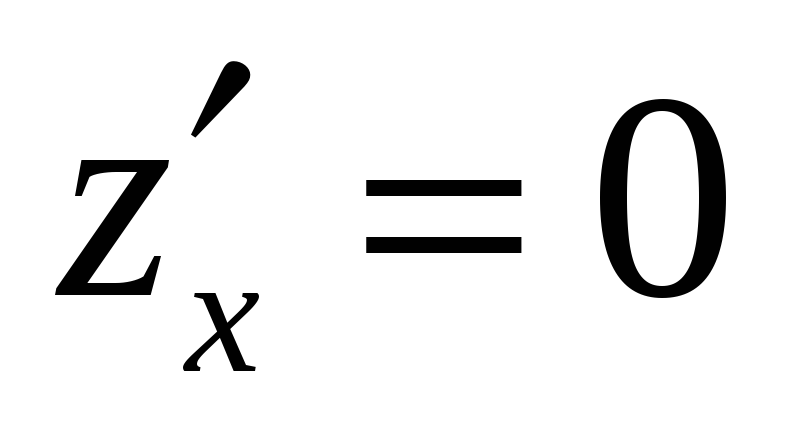 ,
,
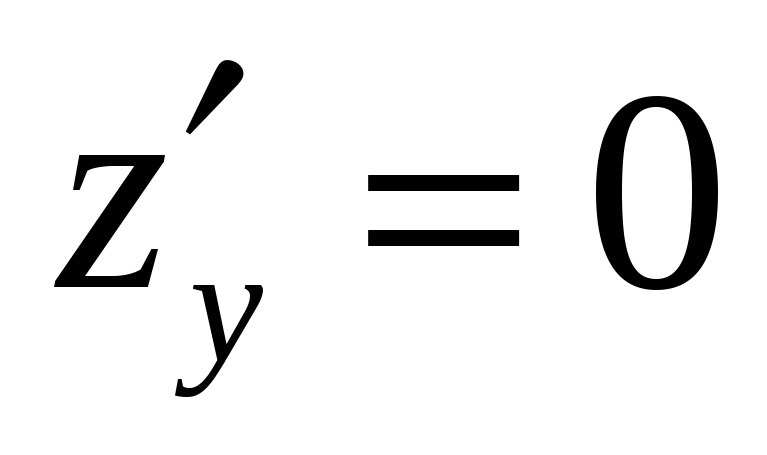 и найти критические точки функции.
и найти критические точки функции. -
Найти частные производные второго порядка, вычислить их значения в каждой критической точке и с помощью достаточного условия сделать вывод о наличии экстремумов.
-
Найти значения функции в точках экстремума.
Пример
1. Исследовать
на экстремум функцию
![]() .
.
Решение.
1)
![]()
![]()
2)
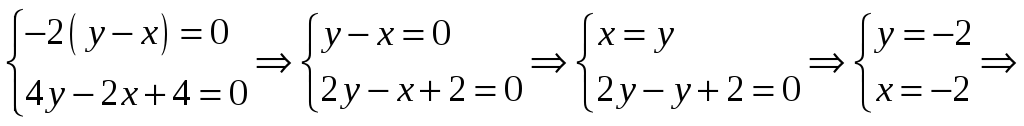 т.
М(-2; -2) –
т.
М(-2; -2) –
критическая точка.
3)
![]() .
.
![]() в
точке М(-2; -2) существует экстремум.
в
точке М(-2; -2) существует экстремум.
![]() минимум
минимум
4)
![]() .
.
Ответ:
![]() .
.
Пример
2. Исследовать
на экстремум функцию
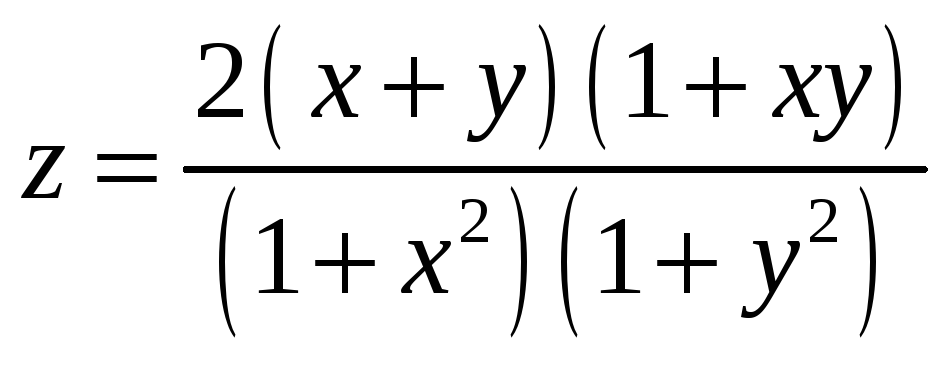 .
.
Решение. 1) Преобразуем функцию:
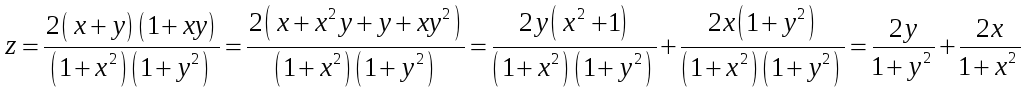 .
.
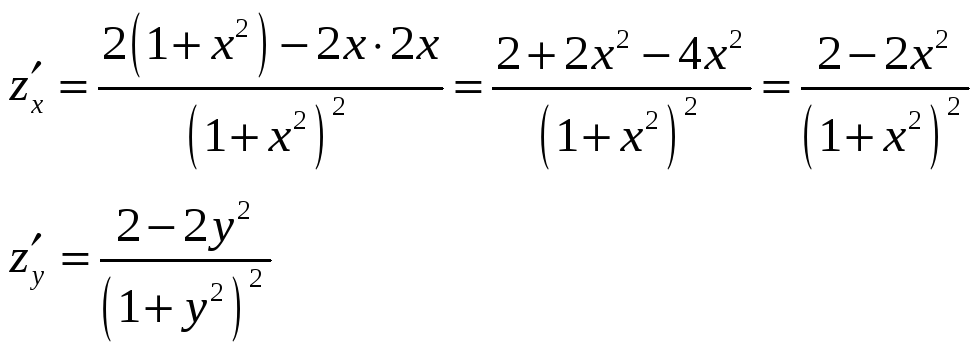
2)
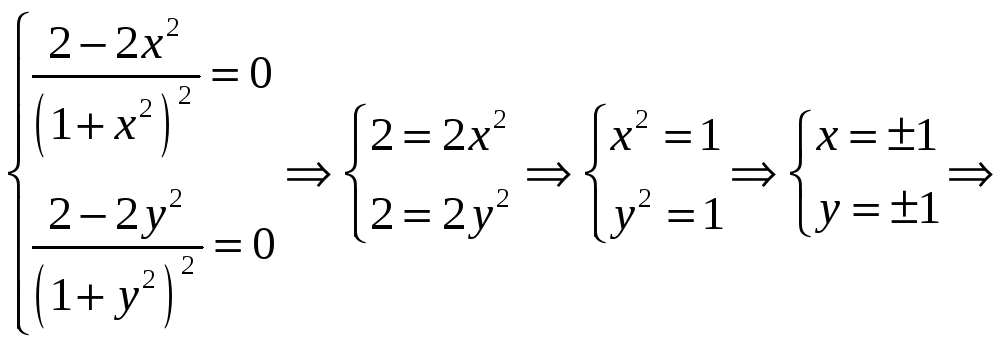
критические
точки
![]() .
.
3)
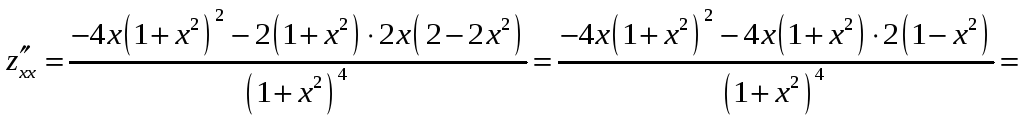
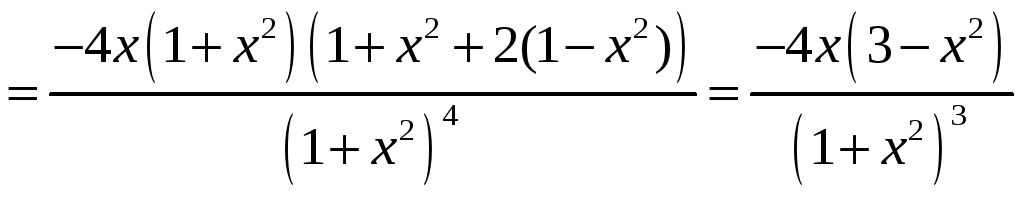

Для
точки
![]() :
:
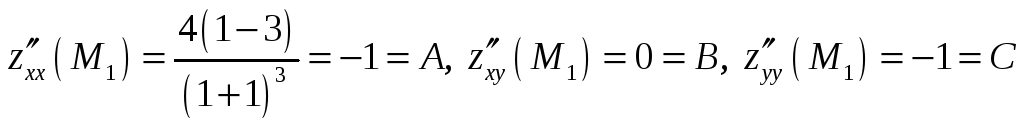
![]() в
точке
в
точке
![]() существует экстремум,
существует экстремум,
![]() максимум.
максимум.
Для
точки
![]() :
:
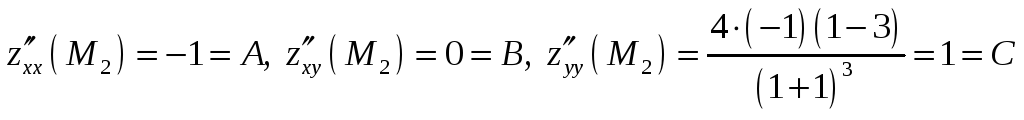
![]() в
точке
в
точке
![]() нет экстремума.
нет экстремума.
Для
точки
![]() :
:
![]()
![]() в
точке
в
точке
![]() нет экстремума.
нет экстремума.
Для
точки
![]() :
:
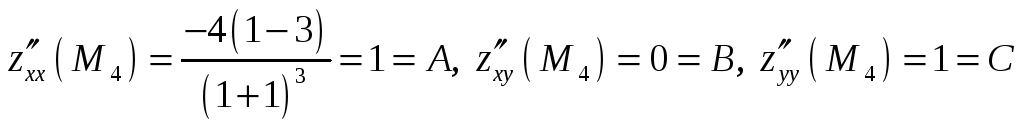
![]() в
точке
в
точке
![]() существует экстремум,
существует экстремум,
![]() минимум.
минимум.
4)
![]()
