
- •7. Определённый интеграл Понятие определённого интеграла
- •Интегрирование по частям в определённом интеграле
- •Вычисление площадей плоских фигур
- •Вычисление объёмов тел вращения
- •Несобственные интегралы
- •8. Числовые ряды
- •Свойства сходящихся рядов
- •Необходимый признак сходимости
- •Ряды с положительными членами. Признаки сходимости
- •Знакочередующиеся числовые ряды
- •Знакопеременные ряды
- •9. Степенные ряды
- •Область сходимости степенного ряда
- •Свойства степенных рядов
- •Ряд Маклорена
- •Применение рядов в приближённых вычислениях
- •10. Функции нескольких переменных
- •Предел и непрерывность
- •Частные производные
- •Дифференциал функции
- •Градиент
- •Производная по направлению
- •Частные производные высших порядков
- •11. Исследование функции нескольких переменных Экстремум функции нескольких переменных
- •Наибольшее и наименьшее значения функции двух переменных
- •Условный экстремум
- •Метод множителей Лагранжа
- •12. Общие понятия теории дифференциальных уравнений. Дифференциальные уравнения 1-го порядка
- •Уравнения с разделяющимися переменными
- •Однородные уравнения
- •Линейные уравнения
- •Уравнения в полных дифференциалах
- •13. Дифференциальные уравнения высших порядков Основные понятия и определения
- •Уравнения, допускающие понижение порядка
- •Линейные дифференциальные уравнения второго порядка
- •Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами
- •Линейные неоднородные дифференциальные уравнения второго порядка с постоянными коэффициентами
- •Метод вариации произвольных постоянных
10. Функции нескольких переменных
Пусть имеется n переменных величин, и каждому набору их значений (х1, х2, …, хn) из некоторого множества Х соответствует одно вполне определенное значение переменной величины z. Тогда говорят, что задана функция нескольких переменных z = f(х1, …, хn).
Переменные х1, …, хn называются независимыми переменными или аргументами, z – зависимой переменной, а символ f означает закон соответствия. Множество Х называется областью определения функции. Очевидно, что это подмножество n-мерного пространства.
Функция двух переменных будем обозначается z = f(x, y). Её область определения Х есть подмножество координатной плоскости Оху.
Окрестностью
точки
![]() называется круг, содержащий точку М0.
Круг на плоскости – двумерный аналог
интервала на прямой.
называется круг, содержащий точку М0.
Круг на плоскости – двумерный аналог
интервала на прямой.
Графиком функции двух переменных z = f(x, y) называется множество точек трехмерного пространства (х, у, z), аппликата z которых связана с абсциссой х и ординатой у функциональным соотношением z = f(x, y).
График функции двух переменных z = f(x, y) представляет собой некоторую поверхность в трехмерном пространстве.
Для построения графика функции z = f(x, y) полезно рассматривать функции одной переменной z = f(x, y0) и z = f(x0, y), представляющие сечения графика z = f(x, y) плоскостями Охz и Oyz, т.е. плоскостями y = y0 и х = х0.
Пример
1. Построить
график функции
![]() .
.
Решение.
Сечения поверхности
![]() плоскостями, параллельными координатным
плоскостям Oyz
и
Охz, представляют
параболы (например, при
плоскостями, параллельными координатным
плоскостям Oyz
и
Охz, представляют
параболы (например, при
![]() ,
при
,
при
![]() и т.д.). В сечении поверхности координатной
плоскостью Оху,
т.е. плоскостью z
= 0, получается окружность
и т.д.). В сечении поверхности координатной
плоскостью Оху,
т.е. плоскостью z
= 0, получается окружность
![]() .
График функции представляет поверхность,
называемую параболоидом.
.
График функции представляет поверхность,
называемую параболоидом.
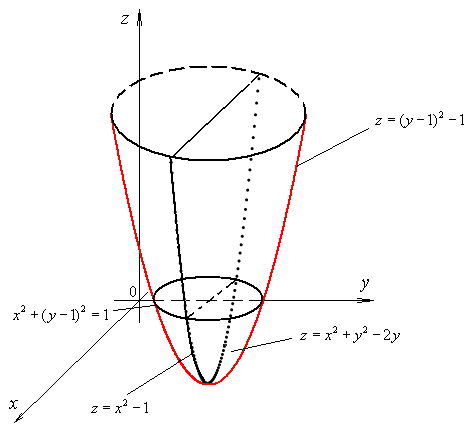
График функции двух переменных – значительно более сложный объект, чем график функции одной переменной. Как правило, построение поверхности оказывается довольно трудной задачей. В то же время, поверхность в пространстве обладает гораздо меньшей наглядностью, чем линия на плоскости. Поэтому в случае двух переменных для изучения поведения функции желательно использовать другие, более наглядные инструменты. Важнейшим из них являются линии уровня.
Линией уровня функции двух переменных z = f(x, y) называется множество точек на плоскости, таких, что во всех этих точках значение функции одно и то же и равно С.
Предел и непрерывность
Число
А
называется пределом функции z
= f(x,
y)
при
![]() и
и
![]() (или в точке (x0,
y0)),
если для любого, даже сколь угодно малого
положительного числа
(или в точке (x0,
y0)),
если для любого, даже сколь угодно малого
положительного числа
![]() ,
найдется положительное число
,
найдется положительное число
![]() (зависящее от ε,
(зависящее от ε,
![]() ),
такое, что для всех точек (x,
y),
отстоящих от точки (x0,
y0)
на расстояние ρ
меньше, чем δ (т.е. при 0 < ρ < δ),
выполняется неравенство
),
такое, что для всех точек (x,
y),
отстоящих от точки (x0,
y0)
на расстояние ρ
меньше, чем δ (т.е. при 0 < ρ < δ),
выполняется неравенство
![]() .
.
Обозначается
предел так:
![]() .
.
Функция z = f(x, y) называется непрерывной в точке (x0, y0), если она:
1)
определена в точке (x0,
y0);
2) имеет конечный предел при
![]() и
и
![]() ;
;
3)
этот предел равен значению функции в
точке (x0,
y0),
т.е.
![]() .
.
Частные производные
Частной производной функции нескольких переменных по одной из этих переменных называется предел отношения соответствующего приращения функции к приращению рассматриваемой независимой переменной при стремлении последнего к нулю (если этот предел существует).
Обозначается
частная производная так:
![]() или
или
![]() ,
или
,
или
![]() .
.
Для
нахождения производной
![]() надо считать постоянной переменную у,
а для нахождения
надо считать постоянной переменную у,
а для нахождения
![]() - переменную х.
- переменную х.
Пример
2. Найти
частные производные функции
![]() .
.
Решение.
1) Находим частные производные по х.
При этом y
= const:
![]() .
.
2)
Находим частные производные по y.
При этом х
= const:
![]() .
.
Пример
3. Найти
частные производные функции
![]() .
.
![]()
Пример
4. Найти
частные производные функции
![]() .
.
![]()
Пример
5. Найти
частные производные функции
![]() .
.
![]() .
.
