Свойства степенных рядов

Пусть функция является суммой степенного ряда, т.е. . На любом отрезке , целиком принадлежащем интервалу сходимости , функция является непрерывной, а следовательно, степенной ряд можно почленно интегрировать на этом отрезке.

.

В интервале сходимости степенной ряд можно почленно дифференцировать: .

Полученные после дифференцирования или интегрирования ряды имеют тот же радиус сходимости R.

Пример 2. Найти область сходимости ряда

Решение. Находим радиус сходимости ряда: .

Интервал сходимости .

Проверяем сходимость ряда на концах интервала.

ряд сходится по признаку Лейбница.

. Сравним со сходящимся рядом . По предельному признаку сравнения: ряд сходится.

Ответ: область сходимости .

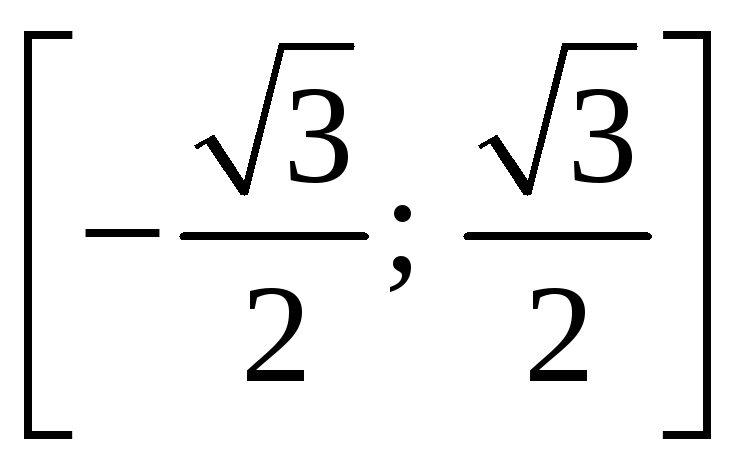Пример 3. Найти область сходимости ряда

Решение. Найти радиус сходимости по формуле в данном случае невозможно, т.к. коэффициенты ряда и т.д. равны нулю. Применим признак Даламбера: .

Следовательно, ряд сходится при или на интервале .

Исследуем сходимость на концах интервала сходимости.

Обе эти ряда расходятся, т.к. не выполняется необходимый признак сходимости.

Ответ: область сходимости .

Ряд Маклорена

Предположим, что функция , определённая и n раз дифференцируемая в окрестности точки х = 0, может быть представлена в виде суммы степенного ряда:

Выразим коэффициенты ряда через . Найдем производную функции , почленно дифференцируя ряд.

Полагая х = 0, получим

. Подставляем значения коэффициентов :

- ряд Маклорена.

Не все функции могут быть разложены в ряд Маклорена. Может оказаться, что ряд расходится или сходится не к функции .

Сумму ряда Маклорена можно представить в виде , где - n-я частичная сумма ряда; - n-й остаток ряда.

Теорема. Для того чтобы ряд Маклорена сходился к функции , необходимо и достаточно, чтобы при остаток ряда стремился к нулю, т.е. для всех значений х из интервала сходимости ряда.

Если функция разложена в ряд Маклорена, то это разложение единственное.

Ряд Маклорена является частным случаем ряда Тейлора:

при .

Ряд Тейлора тесно связан с формулой Тейлора:

где - остаточный член формулы Тейлора: , . При выполнении условия остаток ряда Тейлора равен остаточному члену формулы Тейлора.

Разложение в ряд Маклорена некоторых функций

1. .

Область сходимости ряда

2. .

Область сходимости ряда

3. .

Область сходимости ряда

4. - биномиальный ряд.

Интервал сходимости ряда

5.

Область сходимости ряда

Пример 4. Разложить в ряд функцию .

Решение. Так как , то, заменяя х на , получим:

Применение рядов в приближённых вычислениях

С помощью степенных рядов можно вычислить с заданной степенью точности значения функций, определённых интегралов, которые являются неберущимися или слишком сложными для вычислений, интегрировать дифференциальные уравнения.

Пример 5. Вычислить приближённо с точностью до 0,0001 .

Решение. Запишем ряд при :

Взяв первые 6 членов разложения, для сходящегося знакочередующегося ряда получим погрешность , не превышающую по модулю первого отброшенного члена ряда. .

.

Пример 6. Вычислить приближённо с точностью до 0,0001 .

Решение. Запишем ряд при , входящем в область сходимости ряда :

Возьмём первые 4 члена ряда, так как погрешность в этом случае

Мы учли, что сумма сходящегося геометрического ряда в скобках равна ).

.

Задания для самостоятельного решения

Найти область сходимости ряда:

1. 2.

3. 4.

5. 6. 7.

8. 9. 10.

Разложить в степенной ряд по степеням х функции:

11. 12. 13. 14. 15.

16. 17. 18.

Разложить в ряд Тейлора следующие функции:

19. по степеням 20. по степеням

Вычислить приближённо с точностью до 0,0001:

21. 22. 23. 24. 25. 26. 27.