
- •7. Определённый интеграл Понятие определённого интеграла
- •Интегрирование по частям в определённом интеграле
- •Вычисление площадей плоских фигур
- •Вычисление объёмов тел вращения
- •Несобственные интегралы
- •8. Числовые ряды
- •Свойства сходящихся рядов
- •Необходимый признак сходимости
- •Ряды с положительными членами. Признаки сходимости
- •Знакочередующиеся числовые ряды
- •Знакопеременные ряды
- •9. Степенные ряды
- •Область сходимости степенного ряда
- •Свойства степенных рядов
- •Ряд Маклорена
- •Применение рядов в приближённых вычислениях
- •10. Функции нескольких переменных
- •Предел и непрерывность
- •Частные производные
- •Дифференциал функции
- •Градиент
- •Производная по направлению
- •Частные производные высших порядков
- •11. Исследование функции нескольких переменных Экстремум функции нескольких переменных
- •Наибольшее и наименьшее значения функции двух переменных
- •Условный экстремум
- •Метод множителей Лагранжа
- •12. Общие понятия теории дифференциальных уравнений. Дифференциальные уравнения 1-го порядка
- •Уравнения с разделяющимися переменными
- •Однородные уравнения
- •Линейные уравнения
- •Уравнения в полных дифференциалах
- •13. Дифференциальные уравнения высших порядков Основные понятия и определения
- •Уравнения, допускающие понижение порядка
- •Линейные дифференциальные уравнения второго порядка
- •Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами
- •Линейные неоднородные дифференциальные уравнения второго порядка с постоянными коэффициентами
- •Метод вариации произвольных постоянных
Свойства сходящихся рядов
1.
Если ряд
![]() сходится и имеет сумму S,
то и ряд
сходится и имеет сумму S,
то и ряд
![]() ,
полученный умножением данного ряда на
число λ,
также сходится и имеет сумму λS.
,
полученный умножением данного ряда на
число λ,
также сходится и имеет сумму λS.
2.
Если ряды
![]() и
и
![]() сходятся и их суммы соответственно
равны
сходятся и их суммы соответственно
равны
![]() и
и
![]() ,
то и ряд
,
то и ряд
![]() также сходится, и его сумма равна
также сходится, и его сумма равна
![]() .
.
3. Если ряд сходится, то сходится и ряд, полученный из данного путём отбрасывания (или приписывания) конечного числа членов.
Ряд,
полученный из данного отбрасыванием
его n
первых членов, называется n-м
остатком
ряда:
![]() .
.
![]()
4.
Для того
чтобы ряд
![]() сходился, необходимо и достаточно, чтобы
при
сходился, необходимо и достаточно, чтобы
при
![]() остаток ряда стремился к нулю, то есть
остаток ряда стремился к нулю, то есть
![]() .
.
Необходимый признак сходимости
Теорема.
Если ряд сходится, то предел его общего
члена
![]() при
при
![]() равен нулю:
равен нулю:
![]() .
.
Пример
2. Проверить
выполнение необходимого признака
сходимости для ряда
![]() .
.
![]() необходимый
признак сходимости выполнен.
необходимый
признак сходимости выполнен.
Следствие
из необходимого признака сходимости.
Если предел общего члена ряда при
![]() не равен 0, т.е.
не равен 0, т.е.
![]() ,
то ряд расходится.
,
то ряд расходится.
Пример
3. Исследовать
сходимость ряда
![]() .
.
![]() необходимый
признак сходимости не выполняется
необходимый
признак сходимости не выполняется
![]() ряд расходится.
ряд расходится.
Теорема
выражает лишь необходимый, но не
достаточный признак сходимости ряда.
Если
![]() ,
то из этого ещё не следует, что ряд
сходится.
,
то из этого ещё не следует, что ряд
сходится.
Ряды с положительными членами. Признаки сходимости
Первый признак сравнения. Даны два ряда с положительными членами
![]() и
и
![]() ,
и выполняется неравенство
,
и выполняется неравенство
![]() .
Если сходится ряд
.
Если сходится ряд
![]() ,
то сходится и ряд
,
то сходится и ряд
![]() .
Если расходится ряд
.
Если расходится ряд
![]() ,
то расходится и ряд
,
то расходится и ряд
![]() .
.
Для сравнения с данным рядом используются эталонные ряды.
1.
Геометрический ряд
![]() - сходится при
- сходится при
![]() ,
расходится при
,
расходится при
![]() .
.
2.
Гармонический ряд
![]() - расходится.
- расходится.
3.
Обобщённый гармонический ряд
![]() - сходится при
- сходится при
![]() ,
расходится при
,
расходится при
![]() .
.
Второй
признак сравнения (предельный).
Если
![]() и
и
![]() - ряды с положительными членами и
существует конечный предел отношения
их общих членов
- ряды с положительными членами и
существует конечный предел отношения
их общих членов
![]() ,
то ряды одновременно сходятся, либо
одновременно расходятся.
,
то ряды одновременно сходятся, либо
одновременно расходятся.
Пример
4. исследовать
сходимость ряда
![]() .
.
Решение.
Сравним этот
ряд с расходящимся гармоническим рядом
![]() .
.
(Выбор
основан на том, что при больших значениях
n
![]() ).
).
Применим
второй (предельный) признак сравнения:
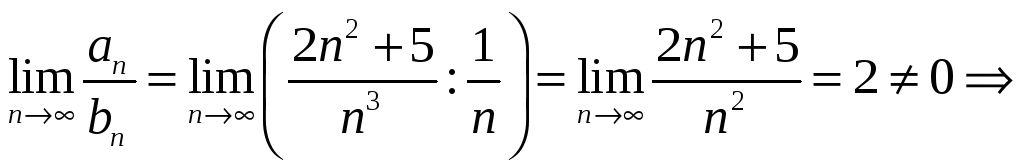 данный
ряд, как и гармонический, расходится.
данный
ряд, как и гармонический, расходится.
Пример
5. исследовать
сходимость ряда
![]() .
.
Решение.
Сравним этот
ряд с геометрическим рядом
![]() ;
;
![]() ряд сходится.
ряд сходится.
Применим
первый признак сравнения:
![]() ряд
ряд
![]() сходится.
сходится.
Признак
Даламбера.
Пусть
![]() - ряд с положительными членами.
- ряд с положительными членами.
Если
![]() ,
ряд сходится. Если
,
ряд сходится. Если
![]() ,
ряд расходится.
,
ряд расходится.
Если
![]() ,
то вопрос о сходимости ряда остаётся
открытым, требуются дополнительные
исследования.
,
то вопрос о сходимости ряда остаётся
открытым, требуются дополнительные
исследования.
Пример
6. Исследовать
сходимость ряда
![]() .
.
Решение.
Применим признак Даламбера, для этого
найдем n+1-й
член ряда:
![]() .
.
![]() ряд
сходится.
ряд
сходится.
Пример
7. Исследовать
сходимость ряда
![]() .
.
Решение.
Применим
признак Даламбера.
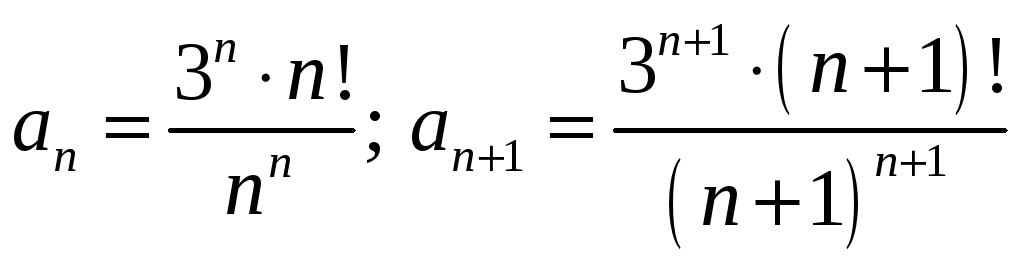 .
.
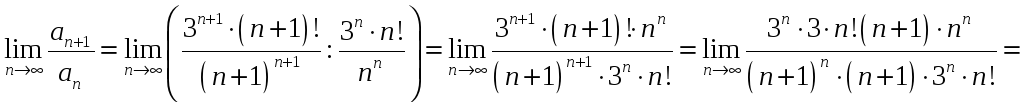
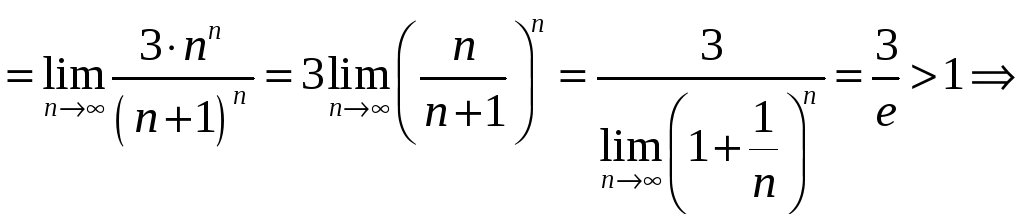 ряд
расходится.
ряд
расходится.
Интегральный признак сходимости
Дан
ряд
![]() с положительными членами, для которых
выполняется
с положительными членами, для которых
выполняется
![]() ,
и функция
,
и функция
![]() ,
определённая при
,
определённая при
![]() ,
непрерывная и невозрастающая, и
,
непрерывная и невозрастающая, и
![]() .
Тогда для сходимости ряда
.
Тогда для сходимости ряда
![]() необходимо и достаточно, чтобы сходился
несобственный интеграл
необходимо и достаточно, чтобы сходился
несобственный интеграл
![]() .
.
Пример
8. Исследовать
сходимость обобщенного гармонического
ряда
![]() .
.
Решение.
Применим интегральный признак сходимости.
Рассмотрим функцию
![]() .
При х >
0 (а значит и при
.
При х >
0 (а значит и при
![]() )
положительная и невозрастающая. Вычислим
несобственный интеграл
)
положительная и невозрастающая. Вычислим
несобственный интеграл
![]()
если
![]() ,
то
,
то
![]()
если
![]() ,
то
,
то
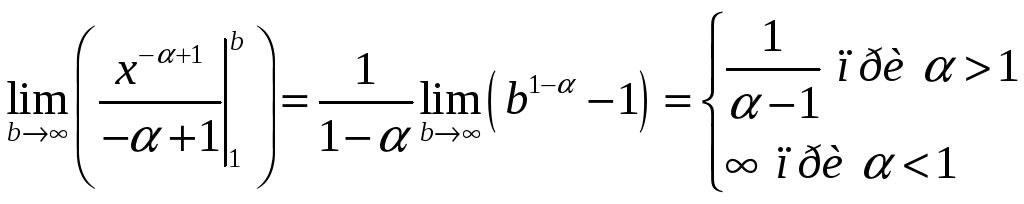
![]() ряд
сходится при
ряд
сходится при
![]() ,
расходится при
,
расходится при
![]() .
.
Пример
9. Исследовать
сходимость ряда
![]() .
.
Решение.
Функция
![]() при х >
0 положительная и невозрастающая.
Вычислим несобственный интеграл:
при х >
0 положительная и невозрастающая.
Вычислим несобственный интеграл:
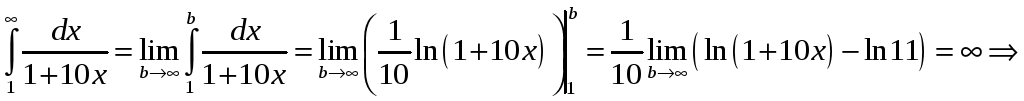 данный
ряд расходится.
данный
ряд расходится.
Признак Коши
Пусть
![]() - ряд с положительными членами.
- ряд с положительными членами.
Если
![]() ,
ряд сходится. Если
,
ряд сходится. Если
![]() ,
ряд расходится.
,
ряд расходится.
Если
![]() ,
то вопрос о сходимости ряда остаётся
открытым, требуются дополнительные
исследования.
,
то вопрос о сходимости ряда остаётся
открытым, требуются дополнительные
исследования.
Пример
10. Исследовать
сходимость ряда
![]() .
.
Решение. Воспользуемся признаком Коши:
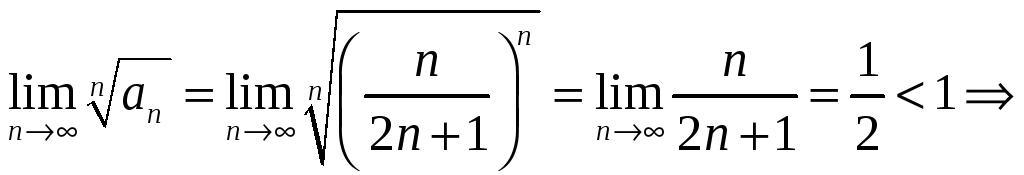 ряд
сходится.
ряд
сходится.
