
- •7. Определённый интеграл Понятие определённого интеграла
- •Интегрирование по частям в определённом интеграле
- •Вычисление площадей плоских фигур
- •Вычисление объёмов тел вращения
- •Несобственные интегралы
- •8. Числовые ряды
- •Свойства сходящихся рядов
- •Необходимый признак сходимости
- •Ряды с положительными членами. Признаки сходимости
- •Знакочередующиеся числовые ряды
- •Знакопеременные ряды
- •9. Степенные ряды
- •Область сходимости степенного ряда
- •Свойства степенных рядов
- •Ряд Маклорена
- •Применение рядов в приближённых вычислениях
- •10. Функции нескольких переменных
- •Предел и непрерывность
- •Частные производные
- •Дифференциал функции
- •Градиент
- •Производная по направлению
- •Частные производные высших порядков
- •11. Исследование функции нескольких переменных Экстремум функции нескольких переменных
- •Наибольшее и наименьшее значения функции двух переменных
- •Условный экстремум
- •Метод множителей Лагранжа
- •12. Общие понятия теории дифференциальных уравнений. Дифференциальные уравнения 1-го порядка
- •Уравнения с разделяющимися переменными
- •Однородные уравнения
- •Линейные уравнения
- •Уравнения в полных дифференциалах
- •13. Дифференциальные уравнения высших порядков Основные понятия и определения
- •Уравнения, допускающие понижение порядка
- •Линейные дифференциальные уравнения второго порядка
- •Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами
- •Линейные неоднородные дифференциальные уравнения второго порядка с постоянными коэффициентами
- •Метод вариации произвольных постоянных
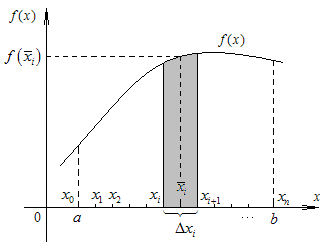
7. Определённый интеграл Понятие определённого интеграла
Пусть
функция
![]() определена и непрерывна на отрезке
определена и непрерывна на отрезке
![]() .
Разобьём отрезок
.
Разобьём отрезок
![]() на n
частей
на n
частей
![]() .
Внутри каждой части
.
Внутри каждой части
![]() выберем точку
выберем точку
![]() и составим сумму вида
и составим сумму вида
![]() .
Пусть
.
Пусть
![]() ,
тогда если существует предел
,
тогда если существует предел
![]() ,
который не зависит от способа разбиения
отрезка
,
который не зависит от способа разбиения
отрезка
![]() и выбора точек
и выбора точек
![]() ,
то он называется определённым
интегралом
от функции
,
то он называется определённым
интегралом
от функции
![]() по отрезку
по отрезку
![]() и обозначается
и обозначается
![]()
а
– нижний предел интегрирования, b
– верхний предел интегрирования,
![]() – подынтегральная функция,
– подынтегральная функция,
![]() – подынтегральное выражение, σ
– интегральная сумма Римана.
– подынтегральное выражение, σ
– интегральная сумма Римана.
Основным
необходимым условием существования
интеграла Римана является ограниченность
функции
![]() на отрезке
на отрезке
![]() .
Отличие неопределённого и определённого
интегралов в том, что неопределённый
интеграл представляет собой семейство
функций, а определённый интеграл является
числом.
.
Отличие неопределённого и определённого
интегралов в том, что неопределённый
интеграл представляет собой семейство
функций, а определённый интеграл является
числом.
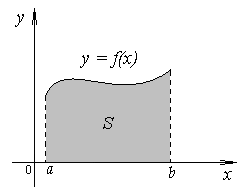
Геометрический смысл определённого интеграла.
Если
функция
![]() неотрицательна на отрезке
неотрицательна на отрезке
![]() ,
где a
< b,
то
,
где a
< b,
то
![]() численно равен площади S
под кривой
численно равен площади S
под кривой
![]() на отрезке
на отрезке
![]() .
.
Экономический смысл определённого интеграла
Если
![]() - производительность труда в момент
времени t,
то
- производительность труда в момент
времени t,
то
![]() - объём выпуска продукции за промежуток
времени
- объём выпуска продукции за промежуток
времени
![]() .
.
Достаточное
условие существования определённого
интеграла
(интегрируемости функции): если функция
![]() непрерывна на отрезке
непрерывна на отрезке
![]() ,
то она интегрируема на этом отрезке.
,
то она интегрируема на этом отрезке.
Свойства определённого интеграла
1.
![]()
2.
![]()
3.
![]() ,
где
,
где
![]() .
.
4.
Если
![]() на
на
![]() ,
то
,
то
![]()
Если
![]() на
на
![]() ,
то
,
то
![]()
5.
![]()
6.
Пусть
![]() - интегрируема на
- интегрируема на
![]() ,
и точка с
такая, что a
< c
< b,
тогда
,
и точка с
такая, что a
< c
< b,
тогда
![]() .
.
Формула Ньютона – Лейбница
Пусть
функция
![]() непрерывна на отрезке
непрерывна на отрезке
![]() и
и
![]() - любая первообразная для
- любая первообразная для
![]() на
на
![]() .
Тогда определённый интеграл от функции
.
Тогда определённый интеграл от функции
![]() на
на
![]() равен приращению первообразной
равен приращению первообразной
![]() на этом отрезке:
на этом отрезке:
![]()
![]()
Пример
1. Вычислить
интеграл
![]() .
.
Решение.
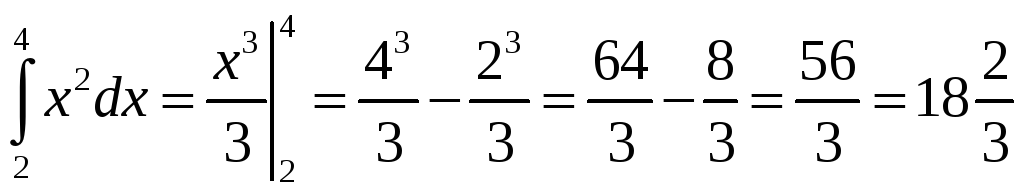 .
.
Замена переменной в определённом интеграле
Пусть
![]() непрерывна на
непрерывна на
![]() .
.
![]() ,
где
,
где
![]() - непрерывная функция вместе со своей
производной
- непрерывная функция вместе со своей
производной
![]() ;
;
![]() ;
;
![]() ,
тогда
,
тогда
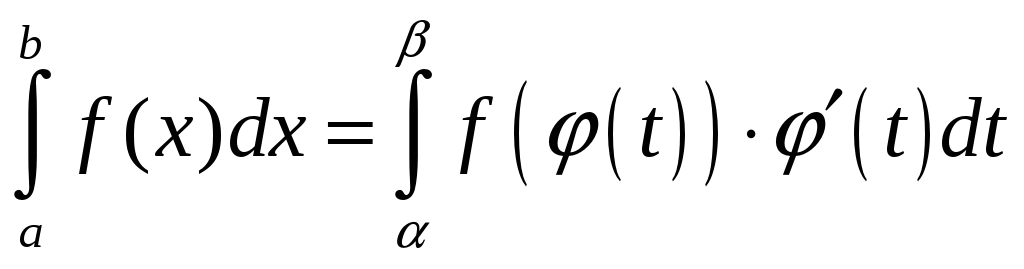 .
.
При
введении новой переменной изменяются
пределы интегрирования, т.н., если
![]() ,
то для вычисления нового нижнего предела
нужно задать
,
то для вычисления нового нижнего предела
нужно задать
![]() и из уравнения
и из уравнения
![]() выразить
выразить
![]() .
Для вычисления верхнего предела:
.
Для вычисления верхнего предела:
![]() .
.
При использовании замены переменной необходимо, чтобы направления изменений x и t совпадали.
Пример
2. Вычислить
интеграл
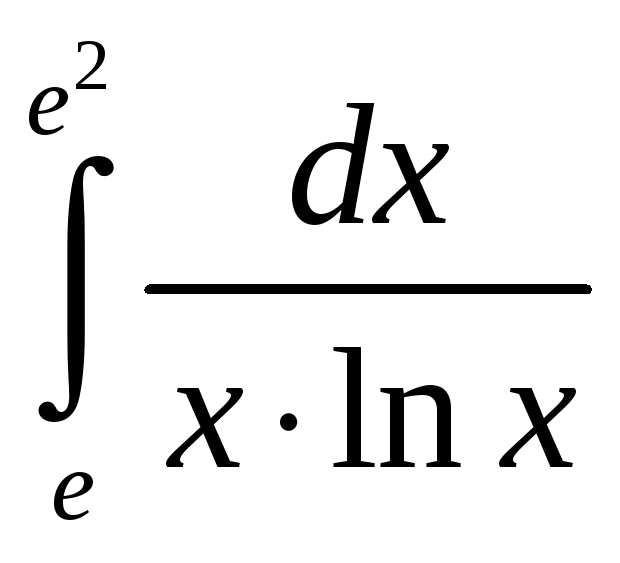 .
.
Решение.
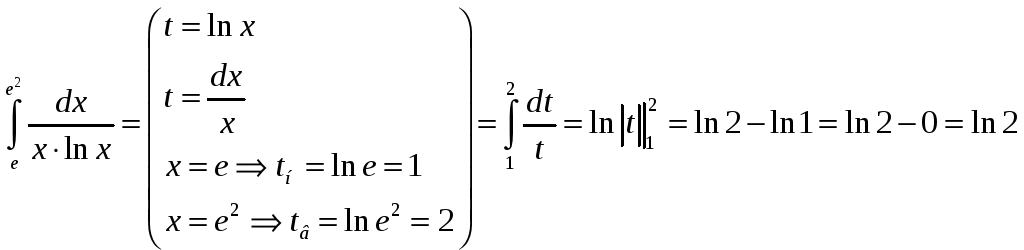 .
.
Интегрирование по частям в определённом интеграле
Формула
интегрирования по частям для определенного
интеграла имеет вид:
![]() .
Рекомендации по выбору u
и dv
остаются точно такими же, как и для
формулы интегрирования по частям в
неопределённом интеграле.
.
Рекомендации по выбору u
и dv
остаются точно такими же, как и для
формулы интегрирования по частям в
неопределённом интеграле.
Пример
3. Вычислить
интеграл![]() .
.
Решение.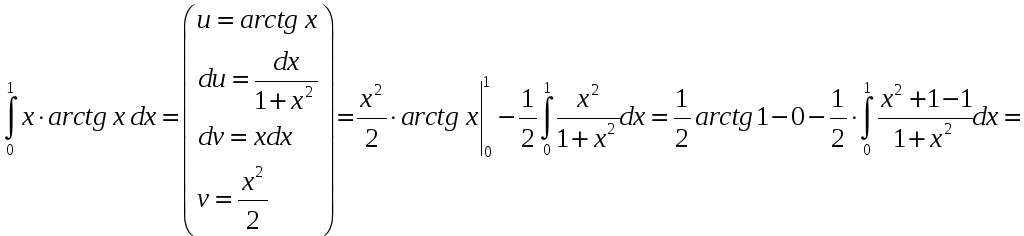
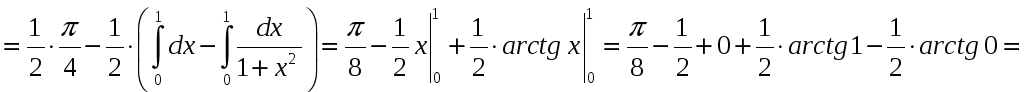
![]() .
.
Вычисление площадей плоских фигур
Из
понятия определённого интеграла следует,
что площадь криволинейной трапеции,
ограниченной сверху графиком кривой
![]() ,
снизу – осью Ох,
с боков – прямыми
,
снизу – осью Ох,
с боков – прямыми
![]() и
и
![]() ,
равна
,
равна
![]() .
.
Если
же необходимо вычислить площадь фигуры,
ограниченной сверху и снизу графиками
функций
![]() и
и
![]() ,
с боков – прямыми
,
с боков – прямыми
![]() и
и
![]() ,
то
,
то
![]() .
.
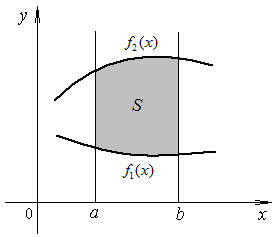
Если
необходимо определить площадь фигуры,
заключённой между двумя кривыми
![]() и
и
![]() ,
то нужно найти точки пересечения этих
кривых, абсциссы которых будут равны a
и b.
,
то нужно найти точки пересечения этих
кривых, абсциссы которых будут равны a
и b.
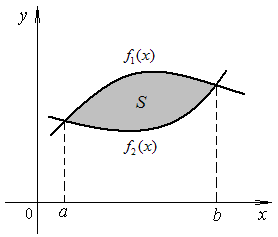
График
функции
![]() может располагаться и ниже оси Ох,
при этом имеют место те же формулы.
может располагаться и ниже оси Ох,
при этом имеют место те же формулы.
Пример
4. Найти
площадь фигуры, ограниченной линиями
![]() ,
,
![]() .
.
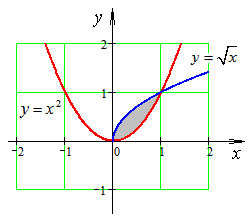
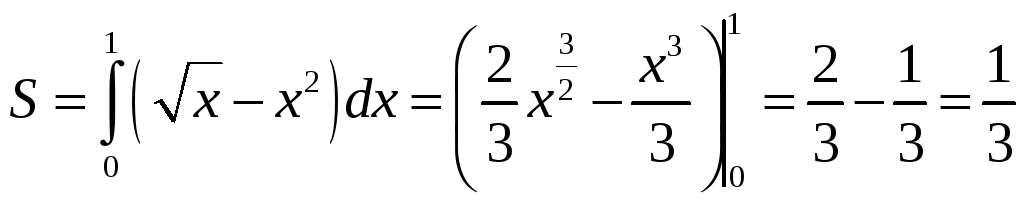 .
.
Иногда бывает удобно поменять функцию, относительно которой происходит интегрирование.
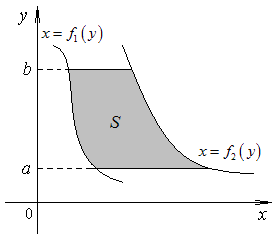
Площадь
фигуры, ограниченной с боков графиками
функций
![]() и
и
![]() ,
сверху и снизу прямыми
,
сверху и снизу прямыми
![]() и
и
![]() ,
вычисляется по формуле:
,
вычисляется по формуле:
![]() .
.
Пример
5. Найти
площадь фигуры, ограниченной графиками
функций
![]() ,
,
![]() .
.
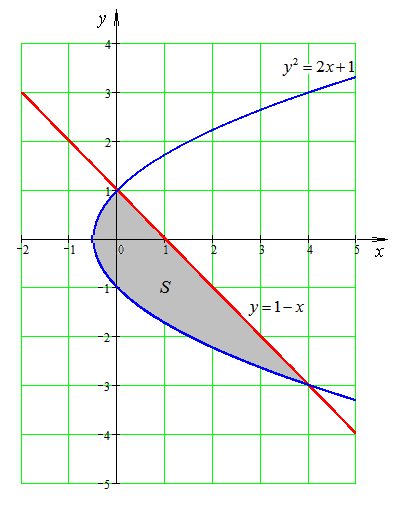
Выразим
х:
![]() .
Для того чтобы найти точки пересечения
кривых, приравниваем значения функций:
.
Для того чтобы найти точки пересечения
кривых, приравниваем значения функций:
![]()
![]() .
.
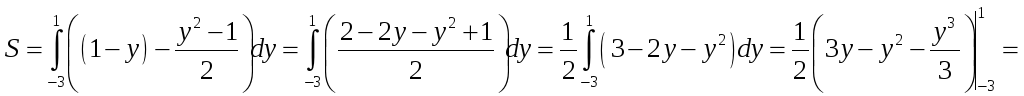
![]() .
.
