лекции / Лекции дсау / ДСАУ 4_4

4. Методы исследования ДСАУ в плоскости z

Синтез ДСАУ с апериодическим процессом______________________________________

4. Синтез ДСАУ с апериодическим процессом

В данном разделе будет рассмотрен метод проектирования цифровой системы с конечным временем переходного процесса.

Рассмотрим цифровую систему, структурная схема которой показана на рис. 1.

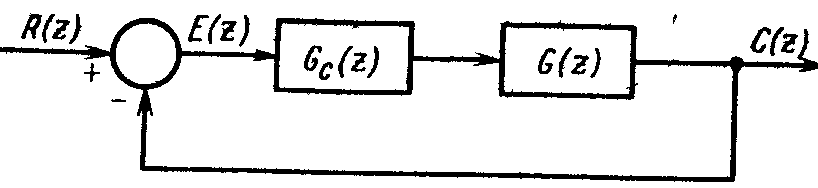
Рис. 1. Цифровая система управления

Пусть передаточная функция управляемого процесса имеет следующий вид

(1)

передаточную функцию последовательного регулятора примем в виде

(2)

как следует из (2), введение регулятора приводит к компенсации всех нулей и полюсов управляемого процесса и к появлению нового полюса z=1. В этом случае передаточная функция разомкнутой системы с коррекцией принимает вид:

(3)

Соответствующая ей передаточная функция замкнутой системы принимает вид

Тогда при ступенчатом входном воздействии z-преобразование выходного сигнала имеет вид

(4)

Это означает, что выходной сигнал системы с (kT) достигает требуемого установившегося значения за один период квантования и с этого момента сохраняет данное значение. Перерегулирование с (kT) равно нулю. Однако| надо иметь в виду, что в действительности о качестве системы следует судить по поведению непрерывной выходной величины c(t). В общем случае, хотя c(kT) может иметь малое перерегулирование или вообще не иметь его, действительная реакция c(t)может сопровождаться пульсациями в промежутках между моментами замыкания.

Поскольку период квантования T =0,1 с намного меньше постоянных времени управляемого процесса, для данной системы можно ожидать, что С (z) или с(kT) довольно хорошо совпадает с c(t). Поэтому есть надежда, что в системе с цифровым регулятором (2) переходная функция достигает установившегося значения, равного единице, за 0,1 с, а в промежутках между моментами замыкания пульсаций не будет или они будут малыми. Такой тип реакции обычно называют апериодическим переходным процессом.

Важно подчеркнуть, что апериодический процесс можно получить только в идеальном случае, когда происходит идеальная компенсация полюсов и нулей. На практике неопределенность полюсов и нулей управляемого процесса, возникающая на стадии его описания, и ограничения в реализации передаточной функции регулятора на ЭВМ приводят к тому, что достигнуть идеального апериодического процесса невозможно.

Подойдем теперь к синтезу систем с апериодическим переходным процессом с общих позиций. Рассмотрим структурную схему системы, изображенную на рис. 1, где G(z) — передаточная функция управляемого процесса, которая может включать и экстраполятор нулевого порядка. Если мы получим критерий синтеза систем с апериодическим переходным процессом, будет ясно, что структура системы не обязательно должна быть такой, как показано на рис.1.

Запишем передаточную функцию замкнутой системы:

(5)

Критерий синтеза характеризуется следующими условиями:

1) система должна иметь в моменты замыкания нулевую установившуюся ошибку при определенном входном сигнале;

2) длительность переходного процесса, определяемая временем достижения установившегося состояния, должна быть минимальной;

3) цифровой регулятор G_c(z) должен быть физически реализуемым.

Разрешая уравнение (5) относительно G_с(z), имеем

(6)

Запишем z-преобразование сигнала ошибки в следующем виде:

(7)

Представим z-преобразование входного сигнала в виде функции

(8)

где N - положительное целое число; A (z) — полином от переменной z^-1, не имеющий нулей z = 1. Например, для единичной ступенчатой функции А (z) = 1 и N = 1; для единичной линейной входной функции А (z) = Tz^-1 и N= 2 и т. д. В общем случае выражение (8) соответствует входным| сигналам типа t^N-1 (см. таблицы z-преобразования непрерывных функций). Приравняем к нулю установившуюся ошибку:

Поскольку полином A (z) не содержит нулей z = 1, то необходимым условием равенства нулю установившейся ошибки является наличие множителя (1 – z^-1)^N в выражении 1 - M(z). Следовательно, последнее должно иметь вид

(9)

где F(z) - полином от переменной z^-1. Разрешая последнее уравнение относительно M(z), получим

(10)

Так как F(z) является полиномом от z^-1, то она имеет полюсы только z = . Таким образом, выражение (10) показывает, что характеристическое уравнение системы с нулевой установившейся ошибкой имеет вид

z^p = 0 (11)

где p – положительное число, причем pN.

После подстановки (9) в (7) z-преобразование ошибки принимает вид

(12)

Поскольку и A(z) и F(z) являются полиномами от z^-1, то изображение ошибки E(z), определяемое выражением (12), будет иметь конечное число членов при разложении его в ряд по отрицательным степеням z. Таким образом, если характеристическое уравнение цифровой системы управления имеет вид (11), т.е. все его корни нулевые, то сигнал ошибки будет сводится к нулю за конечное число периодов квантования.

В общем случае F(z) может иметь вид

(13)

где F_n(z) и F_d(z) – полиномы от z, не содержащие полюсов и нулей z=1 и полюсов, для которых |z|>1. Тогда характеристическое уравнение будет иметь вид

z^pF_d(z) = 0 (14)

Условия физической реализуемости. Выражение (10) показывает, что синтез цифровой системы управления с апериодическим переходным процессом при заданном входном воздействии прежде всего связан с выбором функции F(z). Если по этому выражению установлен вид M(z), то передаточная функция цифрового регулятора находится с помощью (6). Однако требование физической реализуемости Gc(z) и тот факт, что G(z) есть передаточная функция реального физического процесса, накладывают ограничения на вид передаточной функции замкнутой системы М(г). В общем случае G(z) и M(z) могут быть представлены разложением в степенной ряд

(15)

(16)

где n0 и k0. Подставляя два последних выражения в выражение передаточной функции регулятора (6), получим

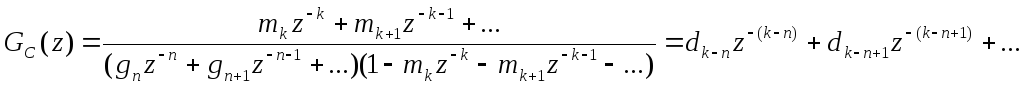
Таким образом, чтобы функция Gc(z) была физически реализуемой, должно выполняться условие k > п, т. е. низшая степень разложения M(z) в ряд относительно переменной z^-1 должна быть во всяком случае не меньше аналогичной (низшей) степени полинома G(z). Тогда выбор функции F(z) при заданном входном воздействии должен производиться на основании соотношения (9) с учетом сформулированного требования к М(z).

Согласно z-преобразованию входного сигнала (8), значение N определяется его видом, т. е. для ступенчатого сигнала N= 1, для линейного сигнала N= 2, для параболического сигнала N=3 и т. д. Связь между общим видом M(z) и типом входного сигнала, необходимая для получения апериодического переходного процесса, устанавливается с помощью соотношения (10). Эта связь отражена в табл. 1.

Анализ табл. 1 показывает, что функция F(z) должна содержать, по крайней мере, слагаемое, равное единице, ибо, если такое слагаемое будет иметь M(z), она не будет физически реализуемой. В действительности, ничто не мешает выбрать F(z) = 1 для всех входных сигналов типа (8). Тогда для трех основных типов входных сигналов, рассмотренных в табл. 1, передаточные функции замкнутой системы с апериодическим переходным процессом будут иметь вид, представленный в табл. 2.

Таблица 1

Входная функция	N	M(z)
Ступенчатая us(t)	1	1 – (1- z-1)F(z)
Линейная tus(t)	2	1 – (1- z-1)2F(z)
Параболическая t2us(t)	3	1 – (1- z-1)3F(z)

Таблица 2

Входной сигнал	M(z)
Ступенчатый	z-1
Линейный	2z-1 - z-2
Параболический	3z-1 - 3z-2 + z-3

Результаты, приведенные в табл. 2, показывают, что при ступенчатой входной функции минимальное время установления нулевой ошибки равно одному, при линейной функции — двум, а при параболической — трем периодам квантования.

Как было показано на примере в начале этого параграфа синтез систем с апериодической реакцией основан на компенсации полюсов и нулей управляемого процесса нулями и полюсами цифрового регулятора и добавлении новых полюсов и нулей в соответствующих местах z-плоскости. Здесь может возникнуть одно затруднение, когда G(z) имеет один нуль или большее число нулей, расположенных на единичной окружности или вне ее, и для компенсации этих нулей потребуется неустойчивый регулятор. Другое затруднение возникает при использовании формулы (6), когда M(z) имеет какое-либо из выражений, представленных в табл. 2. Поскольку член наивысшей степени в M(z) равен z^-1, то M(z)/[ 1—M(z}] всегда будет иметь число полюсов на единицу больше, чем число нулей. Тогда, чтобы Gc (z) была физически реализуемой передаточной функцией, число полюсов G(z) не должно превышать числа ее нулей более, чем на единицу. Само собой разумеется, функция G(z) не может иметь нулей больше, чем полюсов. Например, при ступенчатом входном сигнале M(z) = =z^-1 и в результате (6) на основании (6) имеем

(17)

Отсюда легко получается приведенное выше ограничение на G(z). Итак, мы приходим к выводу, что если G(z) имеет один нуль или более на единичной окружности |z| = 1 (или вне ее) или если число её полюсов более чем на единицу превышает число нулей, то F(z) не может просто равняться 1. Следующий пример как раз иллюстрирует тот случай, когда у G(z) число полюсов превышает число нулей более чем на единицу.

Пример 1. Пусть в цифровой системе, изображенной на рис.1, управляемый процесс описывается передаточной функцией

Требуется спроектировать цифровой регулятор, обеспечивающий апериодический переходный процесс при входном сигнале типа единичной ступенчатой функция.

Поскольку передаточная функция G (z) имеет полюсов на два больше, чем нулей, мы не можем выбрать M(z) = z^-1, так как это приведет к физически нереализуемой функции Gc(z). Попробуем взять М(z) = z^-2. Тогда из (6) имеем

что соответствует физически реализуемой передаточной функции. В данном случае функция F(z) определяется выражением

Можно показать, что в общем случае при заданном входном воздействии, определяющем значение N, минимальное число периодов квантования, необходимое для (Установления нулевой ошибки, равно N+ М, где М + 1 есть разность между числом полюсов и числом нулей передаточной функции управляемого процесса G (z).

Синтез систем с апериодической реакцией при наличии полюсов или нулей управляемого процесса на единичной окружности или вне ее. Мы установили, что синтез цифровых систем управления с апериодической реакцией основан на компенсации полюсов и нулей управляемого процесса дулями и полюсами регулятора. Однако если управляемый процесс имеет полюсы или нули, которые находятся на z-плоскости на единичной окружности или вне ее, то неидеальная компенсация, весьма вероятная на практике, будет приводить к неустойчивости замкнутой системы. Поэтому в подобных случаях и не пытаются прибегать к такой компенсации, а просто накладывают дополнительные ограничения на передаточную .функцию замкнутой системы М (z).

Пусть передаточная функция управляемого процесса, представленного на рис. 1, имеет вид

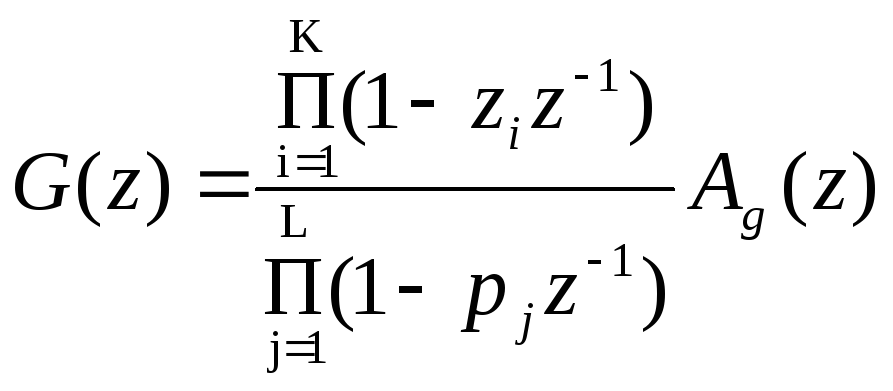(18)

где z_i (i = 1, 2, ..., k) и p_j (j = 1, 2,..., L) есть соответственно нули и полюсы G(z), лежащие на единичной окружности или вне ее, Ag (z) — рациональная функция от z^-1, полюсы и нули которой расположены только внутри единичной окружности. Подстановка (18) в (6) дает

(19)

Поскольку Gc (z) не может иметь p_j и z_i- в качестве своих нулей и полюсов, необходимо предусмотреть их сокращение за счет соответствующих нулей и полюсов функций 1 — M(z) и M(z). Иными словами, функция M(z) должна содержать член

(20)

а функция 1 – M(z) должна содержать

В общем случае M(z) и 1 – M(z) имеют следующий вид:

(21)

(22)

где т должно быть больше или равно низшей степени z^-1 в разложении G(z) в ряд, а целое число N зависит от порядка входного сигнала. Заметим, что если G(z) имеет полюсы z = 1, то сомножитель (1 – z^-1) в выражении 1 - M(z) возводится в степень, равную либо порядку полюсов входного сигнала, либо порядку полюсов z = 1 функции G(z) в зависимости от того, какой из них выше.

Приведенный ниже пример иллюстрирует синтез цифровой системы, в которой управляемый процесс имеет полюсы или нули вне единичной окружности или на ней.

Пример 2. Пусть передаточная функция управляемого процесса имеет вид

(23)

Требуется спроектировать цифровой регулятор, который при линейном входном воздействии обеспечивал бы минимальное время переходного процесса и нулевую установившуюся ошибку.

Поскольку G (z) имеет нуль z = — 2,78 вне единичной окружности и два полюса z = 1 на единичной окружности, то M(z) и 1 - М(г) должны быть выбраны в виде (21) и (22) соответственно. Таким образом,

(24)

Так как первый член разложения G(z) в ряд равен 0,000392 z^-1, то первый член разложения M(z) в ряд должен быть вида M₁z^-1, где М₁ — коэффициент, подлежащий определению. В случае линейной входной функции выражение 1 - M(z) должно содержать множитель (1 - z^-1)², а также множитель, соответствующий всем полюсам G(z), расположенным на единичной окружности или вне ее. Так как G(z) имеет два полюса z =1, то наличие члена (1 – z^-1)² в выражении 1 –M(z) достаточно, чтобы удовлетворить обоим требованиям. Поэтому 1 - M(z) следует выбрать в виде

(25)

где для получения апериодической реакции и одновременно физически реализуемой функции G_c(z) в выражении 1 — M(z) должен присутствовать постоянный член, равный 1, ибо a₁  0. Поскольку M(z) теперь имеет минимальный порядок, равный 3, то переходный процесс будет заканчиваться за три периода квантования, что для данной системы является наименьшим возможным временем установления. Из табл. 2 следует, что если бы функция G(z) не имела полюсов или нулей на единичной окружности или вне ее, то минимальное время установления при линейном входном сигнале было бы равно двум периодам квантования. Из-за наличия у G (z) нуля z = -2,78 функцию F(z} уже нельзя выбирать равной 1, и время установления увеличим на один период квантования. Вообще, чем больше нулей и полюсов G(z) находится на единичной окружности или вне ее, тем больше будет минимальное время установления апериодического переходного процесса.

Теперь получим три независимых уравнения относительно трех неизвестных M₁, M₂, и a₁. Подстановка (24) в (25) дает следующее уравнение:

Приравнивая коэффициенты при соответствующих членах в обеих частях последне­го уравнения, получим

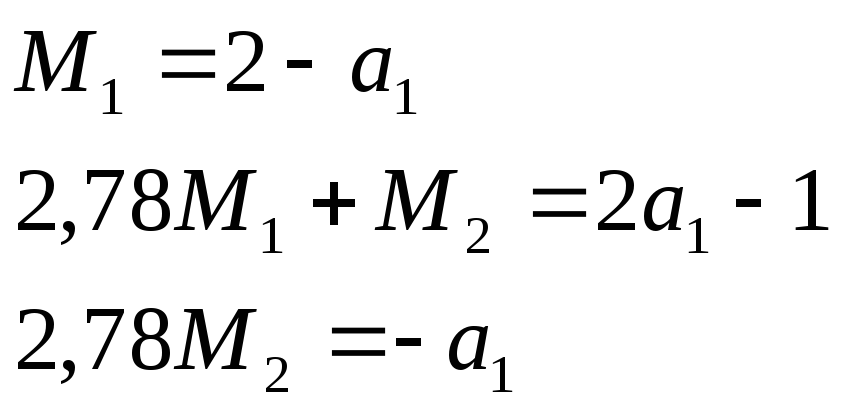
Решение этих уравнений дает следующие коэффициенты: М₁ = 0,723; M₂ = - 0,46; a₀= 1,277. Замкнутая система имеет передаточную функцию

При линейной входной функции с единичным наклоном z-преобразование выходного сигнала имеет вид

Если на вход подана единичная ступенчатая функция, то z-преобразование выходного сигнала имеет вид

Передаточная функция цифрового регулятора принимает вид:

Примечания к синтезу систем с апериодическим переходным процес­сом. Хотя при синтезе системы с апериодическим переходным процессом мы получаем систему, обладающую "идеальной" реакцией на определен­ный тип входного сигнала, в действительности она оказывается "настроен­ной" исключительно на этот сигнал, а по отношению к входным сигналам иного вида будет иметь гораздо худшее или неприемлемое качество. Так, в примере 2 система проектировалась в расчете на линейно меняющий­ся входной сигнал. Выходной сигнал становится равен входному и затем отслеживает его без ошибки спустя три периода квантования. Однако ес­ли на ту же самую систему действует единичная ступенчатая функция, то максимальное значение выходного сигнала равно 2,277, т. е. перерегулиро­вание достигает 127,7%.

Другая проблема возникает в связи с наличием кратного полюса у передаточной функции замкнутой системы M(z), поскольку характеристическое уравнение имеет вид z^N = 0. Можно показать, что чувствитель­ность кратного корня характеристического уравнения к изменению какого-либо параметра системы теоретически равна бесконечности.

6