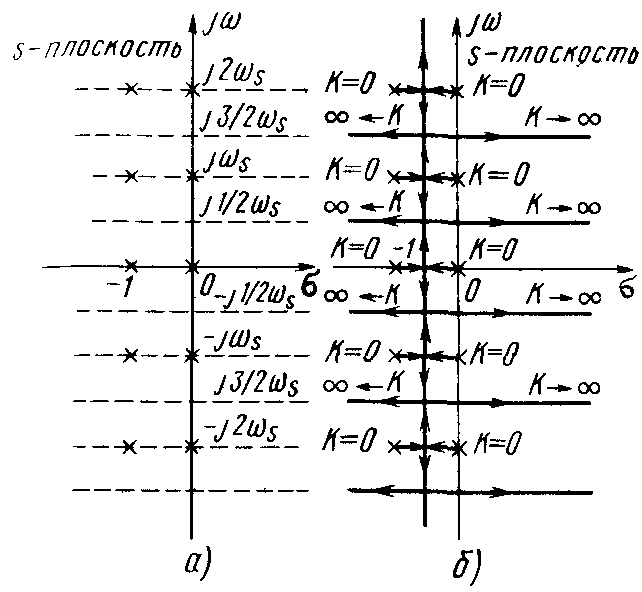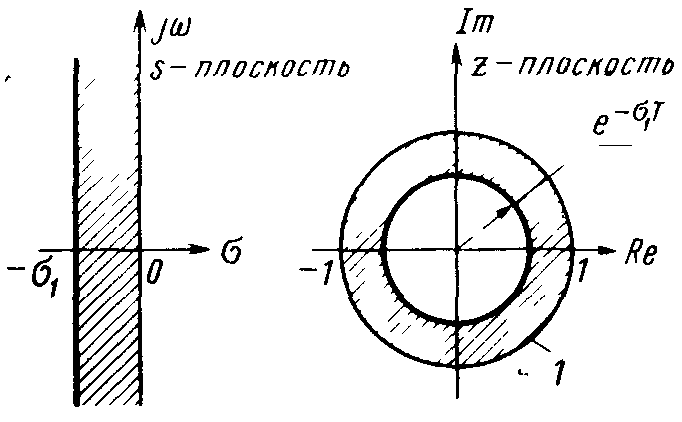лекции / Лекции дсау / ДСАУ 4_5_2

4. Методы исследования ДСАУ в плоскости z

Синтез с использованием корневых годографов__________________________________

Если характеристическое уравнение дискретной системы имеет комплексные корни, расположенные на z-плоскости внутри единичной окружности, то переходная функция системы будет иметь колебательный характер с положительным затуханием. Вообще, чем ближе эти комплексные корни к единичной окружности, тем более колебательным является переходный процесс. Целесообразно установить связь между положением полюсов и нулей передаточной функции замкнутой цифровой системы и максимальным перерегулированием и временем максимума Tmax её переходной характеристики.

Для непрерывной системы второго порядка, имеющей в замкнутом состоянии передаточную функцию вида

C(s) ω_n²

W(s) = —— = ——————— (1)

R(s) s² + 2ξω_ns + ω_n²

максимум переходной характеристики и время этого максимума определяются следующими выражениями:

c_max = 1 + exp(-ξπ / (1-ξ²)); T_max = π / (ω_n (1-ξ²)) (2)

Для систем, порядок которых выше второго, невозможно получить простые соотношения между c_max, T_max и положением полюсов и нулей передаточной функции. Однако, если систему можно охарактеризовать только парой доминирующих полюсов (т.е. полюсов передаточной функции замкнутой системы, которые имеют определяющее значения для переходной характеристики), а остальные полюсы и нули находятся далеко слева на s-плоскости, то влияние последних на переходную характеристику незначительно. При этом условии c_max и T_max можно оценивать выражениями (2), соответствующими передаточной функции (1).

● Рассмотрим, например, следующую передаточную функцию системы четвертого порядка:

C(s) K

W(s) = —— = ————————————— (3)

R(s) (s + p₁)(s + p₂)(s² + 2ξω_ns + ω_n²)

где p₁ и p₂ – действительные константы. Если p₁ и p₂ по крайней мере в 5 раз больше, чем ξω_n, то два полюса в точках - p₁ и - p₂ будут давать незначительный вклад в переходную характеристику, а полюсы

s = - ξω_n + jω_n(1-ξ²) и s = - ξω_n - jω_n(1-ξ²)

являются доминирующими. Однако просто отбросить члены (s + p₁) и (s + p₂) в выражении (3) нельзя, так как они оказывают влияние на качество установившегося режима системы.

4.5.2. Синтез с использованием корневых годографов на z-плоскости

1. Корневые годографы цифровых систем управления

Как известно, корневой годограф непрерывной системы управления, по существу, является диаграммой траектории корней характеристического уравнения как функцией некоторого параметра K, который изменяется от - до +. Корневой годограф дает возможность судить об абсолютной и относительной устойчивости системы управления в зависимости от этого параметра.

Поскольку характеристическое уравнение линейной стационарной цифровой системы управления является рациональным полиномом относительно z, то те же правила, которые используются для построения корневых годографов на s-плоскости, могут быть применены и на z-плоскости. В принципе корневой годограф цифровой системы управления можно построить на s-плоскости, воспользовавшись характеристическим уравнением, полученным из полинома в знаменателе передаточной функции замкнутой системы C*(s)/R*(s), однако он будет содержать бесконечное число ветвей. Чтобы проиллюстрировать трудности анализа цифровых систем на s-плоскости, рассмотрим импульсную передаточную функцию замкнутой цифровой системы управления, заданную в виде

(1)

где G*(s) — дискретная функция от

(2)

Итак,

(3)

Известно, что траектории корней уравнения 1 + G*(s) = 0 могут быть построены на основе информации о полюсах и нулях передаточной функции разомкнутой системы G*(s). В данном случае функция G*(s) имеет бесконечное число полюсов, как показано на рис. 1,а. Следовательно, корневой годограф уравнения 1 + G*(s) = 0 содержит бесконечное число ветвей, как показано на рис. 1,б. Ясно, что для цифровых систем управления с более сложными передаточными функциями построение корневых годографов на s-плоскости будет более трудоемким.

Использование z-преобразования отображает бесконечное число полюсов и нулей, а значит, и траекторий корней на s-плоскости в конечное число на z-плоскости. Для системы, описываемой уравнением (1), преобразование дает

(4)

а корни характеристического уравнения находят путем решения

(5)

где в соответствии с G(s) вида (6-53)

(6)

Теперь траектории корней характеристического уравнения

(7)

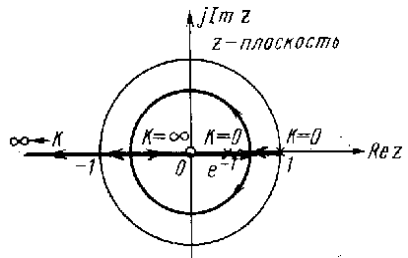
при изменении К от 0 до  выглядят с учетом расположения нулей и полюсов G(z) так, как показано на рис. 2. Поскольку уравнение (7) имеет второй порядок, то корневой годограф на рис. 2 состоит только из двух ветвей.

Рис. 1. Расположение полюсов G* (s) и корневой годограф системы (1) — (3) : а - полюсы G*(s); б — корневой годограф

Рис. 2. Траектории корней характеристического уравнения (7) при изменении К от 0 до 

Если на z-плоскости построен корневой годограф цифровой системы управления, то по траекториям корней можно судить как об абсолютной, так и об относительной устойчивости системы. Условие абсолютной устойчивости требует, чтобы при данной совокупности параметров системы все корни характеристического уравнения лежали на z-плоскости внутри единичной окружности. В то же время расположение корней указывает и на относительную устойчивость. В связи с этим нас интересуют следующие вопросы: Если система устойчива, то насколько она устойчива и как хороша? Удовлетворяет ли качество переходного процесса системы требованиям проектировщика? В частности, мы желаем иметь информацию о некоторых показателях качества таких, как максимальное перерегулирование и время максимума переходной функции, которые тесно связаны с коэффициентом затухания, фактором затухания и собственной частотой колебаний. Таким образом, проблема анализа относительной устойчивости на z-плоскости, по сути дела, сводится к исследованию положения корней характеристического уравнения относительно кривых постоянного фактора затухания, постоянного коэффициента затухания и постоянной частоты. Эти кривые были рассмотрены в п. 3.2.3.

Рис. 3. Линии постоянного фактора затухания на s- и z-шюскостях: 1 - единичная окружность

Кривые постоянного фактора затухания на z-плоскости представляет собой семейство концентрических окружностей с центром в начале координат; радиус окружности, соответствующий фактору затухания σ1, равен e-σ1T. Одна из таких кривых и соответствующая ей линия на s-плоскости показаны на рис. 3. Если при синтезе требуется, чтобы система имела наименьший фактор затухания σ1 или наибольшую постоянную времени 1/σ1, то все корни характеристического уравнения системы должны лежать слева от линии s = - σ1 на s-плоскости и

соответственно внутри окружности |z| = e^-σ1T (σ₁>0) на z-плоскости, как показано на рис.3.

Линии постоянной частоты являются прямыми, исходящими из начала координат z-плоскости под углами θ = ωТ рад относительно положительного направления действительной оси.

Кривые постоянного коэффициента затухания на z-плоскости представляют собой семейство логарифмических спиралей, за исключением случаев ξ = 0 и ξ = 1. Типичные линии постоянного значения ξ для ξ = 0,5 на s- и z-плоскостях изображены на рис. 4. Если при синтезе должен быть обеспечен определенный максимальный коэффициент затухания, то все корни характеристического уравнения должны лежать левее линии постоянного значения ξ на s-плоскости или внутри соответствующей логарифмической спирали нa z-плоскости.

Поскольку большинство систем управления обладают характеристиками типа фильтра нижних частот, то на практике достаточно использовать только основную полосу s-плоскости. Тем самым предполагается, что удовлетворяются условия импульсной теоремы, т.е. высшая частотная составляющая в системе меньше чем 2ωs. Для этого случая на рис. 5 изображены линии постоянного коэффициента затухания для различных значений ξ для положительной половины основной полосы на s-плоскости и соответствующий кривые на z-плоскости. Линии постоянного значения ξ для –ωs/2ω0 являются зеркальным отображением кривых на рис. 5 относительно действительной оси.

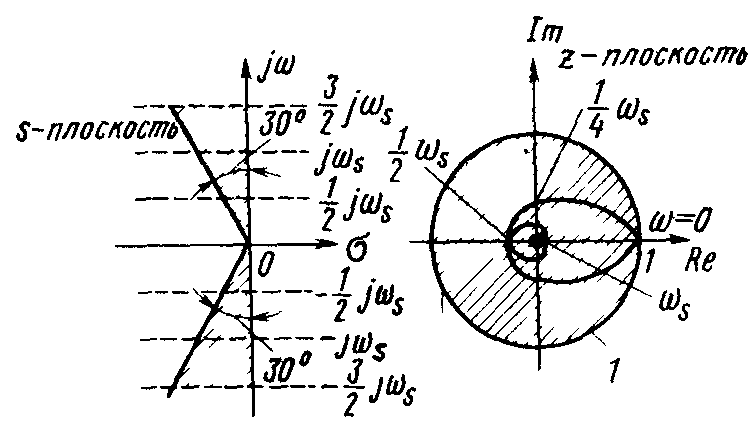
Рис. 4Линии постоянного коэффициента затухания на s- и z-плоскостях для ξ =• 0,5

Рис. 5. Линяй постоянного значения ξ на s-плоскости для периодической полосы от 0 до jω_s/2 (а) и соответствующие этим линиям кривые на z-плоскости(б)

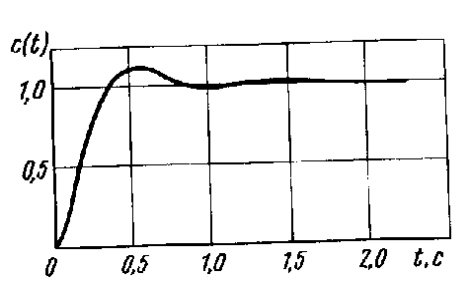
Рис. 6. Корневой годограф цифровой системы	Рис. 7. Переходная функция системы из примера 1

9