Стереографическая проекция

180. Докажите, что число вершин (p), ребер (q) и граней (r) любого выпуклого многогранника связано формулой p–q+r=2.

181. Доказать, что граф правильного многогранника является плоским и правильным.

182. Найти гамильтоновы циклы на правильных графах.

183. При изготовлении некоторой однослойной печатной платы по технологическим условиям один заданный проводник должен находится на краю платы. Доказать, что это всегда можно сделать.

184. Нарисуйте граф, изоморфный графу, изображенному на рисунке, так, чтобы внешней стала грань

• 2

• 3

Двойственные графы

185. Найдите двойственные графы для следующих графов:

186. Покажите, что граф, двойственный к колесу W_n, является колесом.

187. Плоский граф G имеет 7 вершин, 10 ребер и 5 граней. Сколько вершин, ребер и граней имеет двойственный к нему граф.

188. Докажите, что у выпуклого многогранника найдутся две грани с одинаковым числом ребер.

189. Докажите, что не существует выпуклого многогранника, у которого все грани шестиугольники.

190. Может ли существовать плоский граф с пятью гранями, в котором каждая пара граней является смежными?

191. Дан плоский граф, в каждой вершине которого сходится не более трех ребер. Докажите, что

• четное число граней имеет нечетное число смежных граней;

• существует грань, которая имеет не более пяти смежных с ней граней.

Раскраски графа

192. Найдите хроматические числа для:

• вполне несвязного графа с n вершинами;

• полного графа с n вершинами;

• двудольного графа, доли которого имеют n и m вершин;

• дерева с n вершинами.

193. Для графов, изображенных на рисунке, найдите хроматические числа и какую-либо правильную раскраску.

194. Сколькими способами можно раскрасить полный помеченный граф на 6 вершинах шестью цветами? (Два способа считаются различными, если некоторая вершина при одном способе имеет один цвет, а при другом способе – другой.)

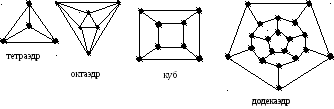
195. Определите хроматические числа для графов платоновых тел:

196. Граф называется критическим, если удаление любой его вершины вместе с инцидентными ей ребрами приводит к графу с меньшим хроматическим числом. Покажите, что К_n, является критическим графом при n >1.

197. Докажите, что всякий критический граф, являющийся k-хроматическим:

• связен;

• не имеет точек сочленения;

• степень каждой его вершины не меньше, чем k–1.

198. Коробка скоростей – механизм для изменения частоты вращения ведомого вала при неизменной частоте вращения ведущего. Это изменение происходит за счет того, что находящиеся внутри коробки шестерни вводятся в зацепление специальным образом. Одна из задач, стоящих перед конструктором коробки, заключается в минимизации числа валов, на которых размещаются шестерни.

Некоторые шестерни не должны находиться на одном валу, например, они могут быть в зацеплении или их общий вес велик для одного вала, и т.д. В таблице крестиками указаны такие пары шестерен. Найдите минимальное число валов, на которые можно поместить шестерни.

	1	2	3	4	5	6	7
1		+		+	+		+
2	+		+		+		+
3		+			+	+
4	+					+
5	+	+	+				+
6			+	+			+
7	+	+			+	+

199. Образовавшийся коммерческий университет арендует здание для проведения занятий. В четверг проводится 7 лекций: право, английский язык, французский язык, экономика, менеджмент, маркетинг, этикет. Чтение каждой лекции в отдельности занимает один час, но некоторые лекции не могут читаться одновременно. В таблице крестиком помечены лекции, которые не могут читаться одновременно. Определите минимальное время, за которое могут быть прочитаны лекции в четверг.

     	П	А	Ф	Э	М	М	Э
     Право		+		+			+
     Англ. яз.	+		+		+	+
     Фран. яз.		+			+	+	+
     Экономика	+				+	+
     Менеджмент		+	+	+		+
     Маркетинг		+	+	+	+
     Этикет	+		+

200. Задача распределения оборудования. Заданы множество работ и механизмов. Для выполнения каждой из работ требуются некоторое время, одинаковое для всех работ, и некоторые механизмы. При этом ни один из механизмов не может быть одновременно занят в нескольких работах. Нужно распределить механизмы так, чтобы общее время выполнения всех работ было минимально.

201. Все страны, расположенные на острове, имеют форму треугольников, причем любые две граничащие страны имеют целую общую сторону (то есть вершина одного треугольника не может лежать на стороне другого). Докажите, что для раскраски карты этого острова так, чтобы никакие две соседние страны не были окрашены в один цвет, достаточно трех красок.

202. Известно, что на карте некоторой области нет точек, в которых сходятся границы нечетного числа районов. Докажите, что такую карту можно раскрасить двумя цветами так, что любые два соседних района будут покрашены разными красками.

203. Докажите, что для раскраски карты, полученной при пересечении прямых и окружностей на плоскости, достаточно двух цветов.