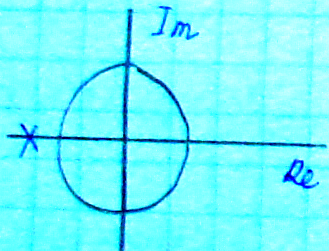12.2. Аналог критерия Михайлова для дискретных сау

В теории дискретных систем разработаны критерии устойчивости, которые являются аналогами критериев устойчивости непрерывных систем. Частотная характеристика дискретных систем получается из ее передаточной функции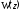путем подстановки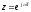

Критерий основан на рассмотрении характеристического полинома:

По выражению 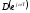можно построить кривую Михайлова.

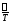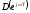Формулировка: Замкнутая дискретная система будет устойчива при возрастании частоты от 0 до, если криваяобходит последовательно в положительном направлении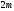квадрантов, где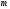- степень характеристического полинома.

По построенному рисунку можно вывести необходимые условия устойчивости дискретных систем:

Для четных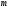

Для нечетных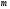

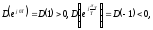
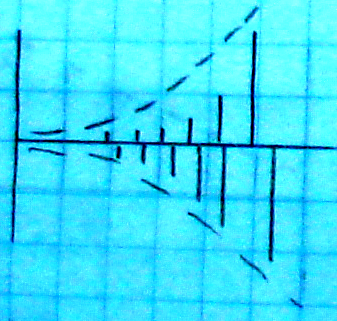
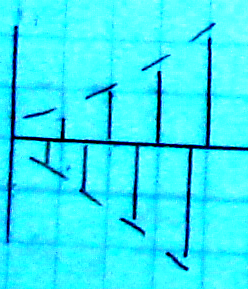
13.2. Виды переходных процессов в импульсных системах

Вид переходного процесса зависит от расположения корней характеристического полинома

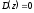
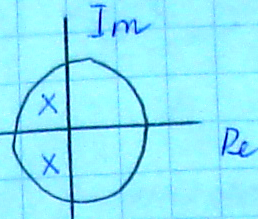
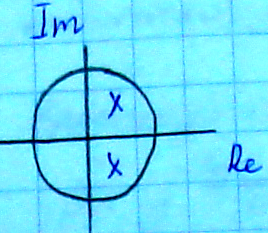
Комплексно сопряженным корням и вещественным отрицательным корням соответствуют колебательные переходные процессы.

Вещественным положительным корням соответствуют монотонные переходные процессы.

Если , то переходные процессы затухающие, если, то расходящиеся.

14.2. Устойчивость дискретных сау

Как и для непрерывных систем необходимым условием является устойчивость, оно означает, что переходный процесс с течением временит должен затухать.

Если считать, что выходная координата

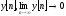
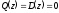- характеристический полином дискретной САУ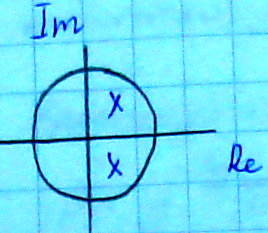

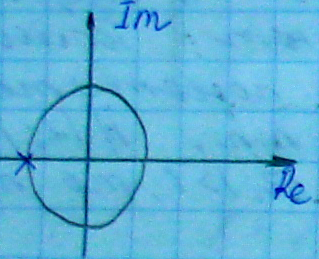
Для выполнения условия устойчивости дискретной САУ необходимо и достаточно, чтобы все корни характеристического полинома замкнутой дискретной системы были по модулю меньше единицы .

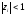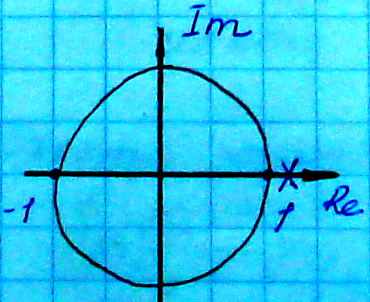
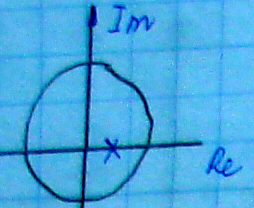
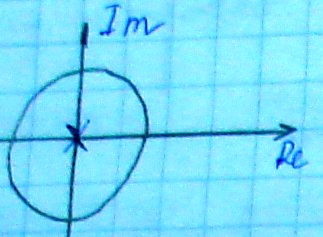
Круг единичного радиуса аналог левой полуплоскости для непрерывных систем.

Так как не всегда удобно решать уравнения высокой степени, то удобнее было бы использовать критерии устойчивости.

Так как для устойчивости непрерывных систем областью устойчивости является левая полуплоскость, а не единичный круг, то применять критерий Найквиста, Михайлова и т.д. к уравнению 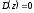неправомерно.

Чтобы иметь такую возможность в характеристическом уравнении переходят к новой переменной , которая связана с переменнойс помощью билинейного преобразования, которое позволяет переходит от области круга к левой полуплоскости.

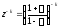
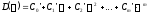
Доказано, что корни этого уравнения будут лежать в левой полуплоскости, если корни уравнения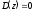лежат в круге единичного радиуса.

Билинейное преобразование отображает круг единичного радиуса в левую полуплоскость параметра , таким образом к новому уравнению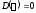теперь можно применять известные критерии устойчивости для непрерывных систем.

В теории дискретных систем разработаны критерии устойчивости, которые являются аналогами критериев устойчивости непрерывных систем. Частотная характеристика дискретных систем получается из ее передаточной функции 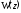путем подстановки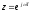

Аналог критерия Михайлова:

Замкнутая дискретная система будет устойчива при возрастании частоты от 0 до 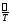, если криваяобходит последовательно в положительном направлении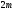квадрантов, где- степень характеристического полинома.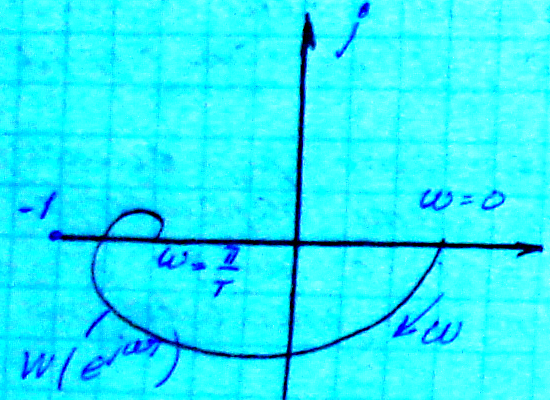

Аналог критерия Найквиста:

Чтобы замкнутая дискретная система, непрерывная часть которой является устойчивой, была тоже устойчива, необходимо и достаточно, чтобы годограф частотной характеристики разомкнутой системы 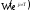при изменении частотыот 0 до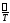не охватывал точку.