8.2. Математическое описание импульсных систем. Разностные уравнения

Импульсная система реагирует на значения воздействия, приложенного ко входу импульсного элемента только в строго определенные моменты времени, равно отстоящие друг от друга, поэтому непрерывное воздействие может быть заменено решетчатой функцией

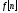
Решетчатая функция определяется в дискретные моменты времени: t=0;T; 2T..nTзначениями непрерывной функции, а в промежутках между этими моментами решетчатая функция равна 0.

_{При обозначении} решетчатой функции параметр Т постоянный и его убирают из выражения, оставляя только

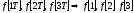
Скорость изменения функции, то есть ее производная определяется её производной первой разностью (аналог первой производной). Первая разность или разность первого порядка обозначается 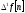и определяется следующим соотношением:

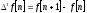
Вторая разность – аналог второй производной:

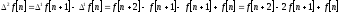
Разность к-го порядка:

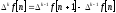
Может быть выражена через решетчатую функцию.

По аналогии с дифференциальными уравнениями для непрерывных систем для дискретных систем можно записать разностные уравнения.

Разностные уравнения - соотношение между решетчатой функцией 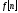и её разностями различных порядков.

Если это соотношение линейно, то и разностное уравнение называется линейным.

Существуют две формы записи линейных разностных уравнений.

1. 

2. 

Дискретные САУ описываются разностными уравнениями, которые можно решить с помощью z- преобразования, которое является основным математическим аппаратом теории дискретных систем

Обычное z- преобразование решетчатой функции 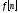называется функция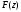, определяющаяся соотношением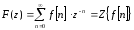, где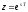- параметр z- преобразования

Модифицированное z- преобразование имеет месть для смещенной решетчатой функции

9.1. Аналитический способ определения параметров периодического движения

САУ позволяет определить и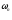из системы управлений:

(*)

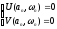где 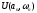,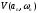вещественная и мнимая составляющие кривой Михайлова:

Если решение системы (*) существует(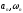- вещественные положительные числа), то, давая приращение амплитуде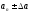, оценивается устойчивость системы. Для найденного периодического решения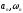кривая Михайлова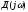проходит через начало координат .Если для положительных приращений амплитуды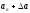, кривая Михайлова займет положение (1), а для отрицательных- положение (2), то найденное решение устойчивое и нелинейная САУ устойчива в «большом».В противном случае найденное решение неустойчивое, система устойчива в малом.

9.2. Виды модуляции в импульсных системах

Импульсной называется система, содержащая по крайней мере один импульсный элемент.

На вход импульсного элемента, осуществляющего квантование, подается непрерывный сигнал, а на его выходе формируется последовательность импульсов, форма которых может быть самой разнообразной. Она зависит от вида модуляции, реализуемой в импульсном элементе. Параметры импульсов изменяются в соответствии со значением входного сигнала и этот процесс их изменения и называется модуляцией.

Различают следующие виды модуляции:

1. Амплитудно-импульсная модуляция (АИМ)

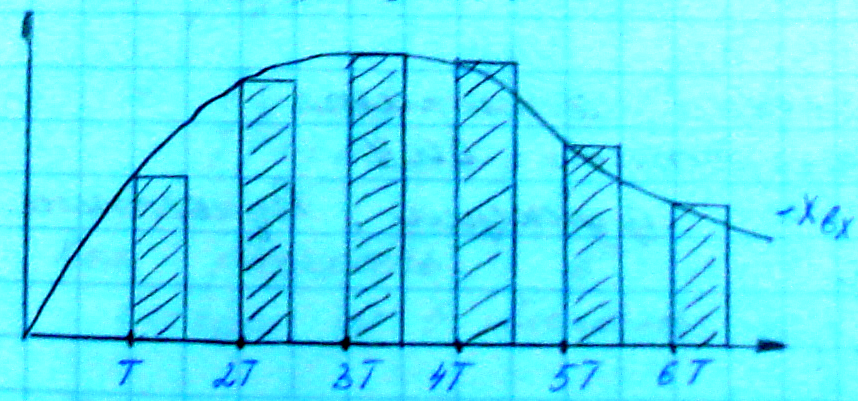
Между импульсами одинаковые расстояния. Ширина импульсов тоже постоянна. Меняется амплитуда импульсов.

2. Широтно-импульсная модуляция (ШИМ)

При этом виде модуляции амплитуда импульсов постоянна, а меняется только ширина импульсов.

3. Частотно-импульсная модуляция (ЧИМ)

4. Время-импульсная (или фазо-импульсная) модуляция (ФИМ)

При АИМ структурную схему системы можно представить :

ИЭ – импульсный элемент

Параметры:

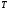- Период квантования

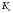Коэффициент усиления по амплитуде

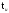Длительность импульса

Относительная длительность импульса