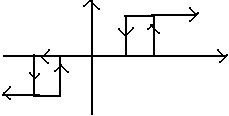
- •2.1. Типовые нелинейные характеристики
- •2.2. Самонастраивающиеся системы со стабилизацией частотных характеристик
- •3.1. Фазовая плоскость. Фазовая траектория. Фазовый портрет.
- •4.1. Фазовый потрет линейной консервативной системы
- •4.2. Адаптивные системы с эталонной моделью
- •5.1. Особые точки фазовых портретов линейной системы второго порядка
- •5.2. Принципы построения контура адаптации
- •6.1. Особые линии фазовых портретов нелинейных систем
- •6.2. Адаптивные системы с сигнальной самонастройкой
- •7.1. Основные положения метода гармонической линеаризации
- •7.2. Классификация адаптивных сау
- •8.1.Гармоничсекий коэффициент передачи нелинейного элемента
- •8.2. Математическое описание импульсных систем. Разностные уравнения
- •9.1. Аналитический способ определения параметров периодического движения
- •9.2. Виды модуляции в импульсных системах
- •10.1. Графический способ определения параметров периодического движения
- •10.2. Виды квантования в импульсных системах
- •11.1. Критерий абсолютной устойчивости Попова
- •11.2. Аналог критерия Найквиста для дискретных сау
- •12.1. Алгоритм анализа устойчивости нелинейных систем на основе критерия Попова
- •12.2. Аналог критерия Михайлова для дискретных сау
- •13.2. Виды переходных процессов в импульсных системах
- •14.2. Устойчивость дискретных сау
11.1. Критерий абсолютной устойчивости Попова
Этот критерий применяется для исследования устойчивости НСАУ с одним нелинейным элементом и устойчивой линейной частью.
Этот критерий является устойчивым.
Критерий достаточный: если он выполняется то система устойчива, если не выполняется, то система может быть как устойчивой, так и неустойчивой.
Для применения этого критерия систему необходимо привести к следующему виду:
|
При однозначной нелинейной характеристике: |
При неоднозначной нелинейной характеристике: |
|
|
|
Формулировка: для того чтобы
положение равновесия нелинейной системы
с устойчивой линейной частью и однозначной
нелинейностью было устойчиво необходимо
и достаточно выполнение следующих
условий:
Действительная часть функции Попова должна быть больше нуля

Нелинейная характеристика должна удовлетворять условию
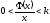
Абсолютная устойчивость проверяется при любых начальных условиях.
Абсолютная устойчивость имеет месть при любой нелинейности внутри сектора

Рассмотрим первое условие о функции Попова:
 ,
,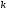 - действительные числа;
- действительные числа;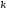 - связывает оба условия критерия.
- связывает оба условия критерия.
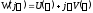 - модифицированный годограф Попова
- модифицированный годограф Попова
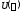 - модифицированная вещественная часть
- модифицированная вещественная часть
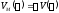 - модифицированная мнимая часть
- модифицированная мнимая часть

Отличие
модифицированной АФЧХ линейной части
от модифицированной АФЧХ заключается
в масштабировании мнимой части в
 раз.
раз.
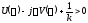 - уравнение прямой
- уравнение прямой
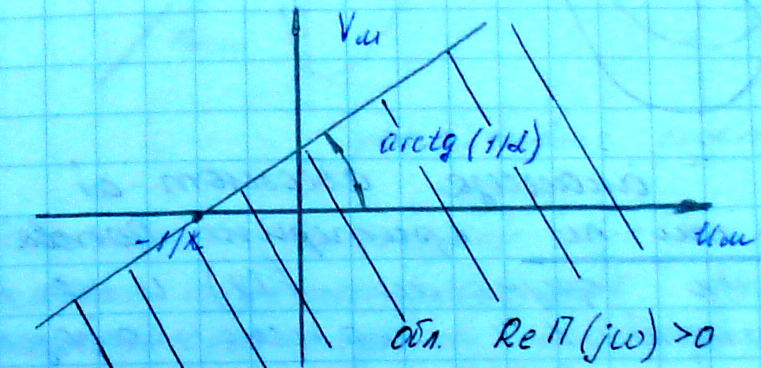
Строим в
плоскости
 прямую Попова.
прямую Попова.
Модифицированный годограф должен лежать справа от прямой:
|
Устойчивая система |
Неустойчивая система |
|
|
|
Если такую прямую невозможно подобрать,
то критерий Попова не выполняется. Если
прямую можно подобрать, то критерий
выполняется и система является абсолютно
устойчивой при любых нелинейностях,
лежащих внутри сектора
 .
.
Невыполнение критерия еще не означает, что равновесие неустойчиво, так как критерий только достаточный, а не необходимый.
Если происходит касание прямой Попова модифицированного годографа, то система устойчива.
11.2. Аналог критерия Найквиста для дискретных сау
В теории дискретных систем разработаны
критерии устойчивости, которые являются
аналогами критериев устойчивости
непрерывных систем. Частотная
характеристика дискретных систем
получается из ее передаточной функции
 путем подстановки
путем подстановки

Формулировка: Чтобы замкнутая
дискретная система, непрерывная часть
которой является устойчивой, была тоже
устойчива, необходимо и достаточно,
чтобы годограф частотной характеристики
разомкнутой системы при изменении частоты
при изменении частоты от
0 до
от
0 до не охватывал точку
не охватывал точку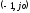 .
.
Удаление характеристики от точки
 характеризует запас устойчивости
системы, как и для непрерывных систем.
характеризует запас устойчивости
системы, как и для непрерывных систем.
12.1. Алгоритм анализа устойчивости нелинейных систем на основе критерия Попова
Формулировка: для того чтобы положение павновесия нелинейной системы с устойчивой линейной частью и однозначной нелинейностью было устойчиво необходимо и достаточно выполнение следующих условий:
Действительная часть функции Попова должна быть больше нуля

Нелинейная характеристика должна удовлетворять условию
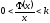

1. Преобразование структурной схемы нелинейной САУ к типовому виду (типовой структурной схеме) по соответствующим правилам.
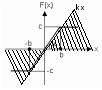
2. Строим график функции
 и на нем проводим линию
и на нем проводим линию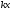 таким образом, чтобы
таким образом, чтобы было минимально и при этом исходная
нелинейность лежала в секторе
было минимально и при этом исходная
нелинейность лежала в секторе
Строим модифицированный годограф Попова
 по
выражению
по
выражению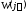 (
( изменяется
от 0 до
изменяется
от 0 до )
)В плоскости
 находим точку
находим точку и пытаемся провести через нее прямую
так, чтобы
и пытаемся провести через нее прямую
так, чтобы полностью лежала справа от прямой.
полностью лежала справа от прямой.
Если такую
прямую невозможно подобрать, то критерий
Попова не выполняется. Если прямую можно
подобрать, то критерий выполняется и
система является абсолютно устойчивой
при любых нелинейностях, лежащих внутри
сектора
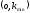 .
.
Невыполнение критерия еще не означает, что равновесие неустойчиво, так как критерий только достаточный, а не необходимый.
Если происходит касание прямой Попова модифицированного годографа, то система устойчива.