Линейные системы с постоянными параметрами

1. Последовательности дискретных сигналов

2. ЛПП – системы

3. Разностные уравнения

4. Частотная характеристика

1. Последовательность дискретных сигналов.

Математики дискретные сигналы представляют в виде непрерывной последовательности чисел:

{h(n)}, {h(nT)}, h(n), h(nT), N₁  n  N₂

При графическом изображении последовательностей используются два способа.

а) в виде отрезка в точке h₀

б) в виде огибающей

Наиболее важные последовательности, используемые при ЦОС:

1. Цифровой единичный импульс (отсчет)

2. Единичный импульс, задержанный на n₀ отсчетов

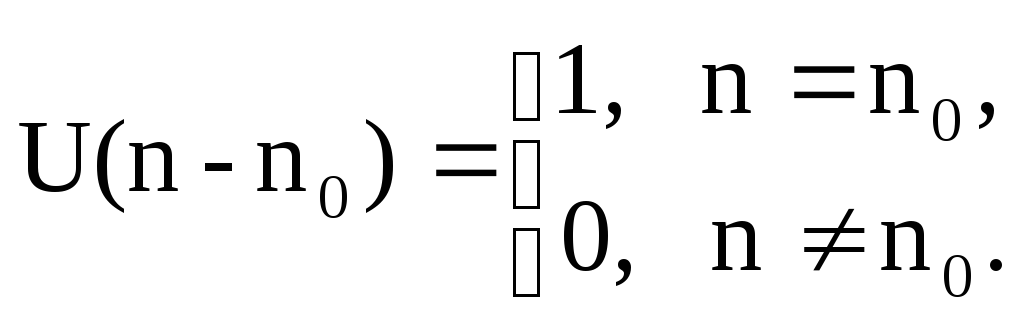
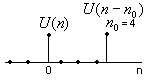
3. Единичный скачок

Единичный скачок связан с единичным импульсом соотношением:

4. Убывающая экспонента

5. Косинусоида

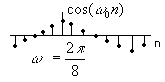для всех n.

6. Комплексная экспонента:

e^jn = cos(n) + jsin(n).

Для ее изображения нужны разделенные графики для действительной и мнимой частей.

7. Произвольная последовательность

a(0), a(1), a(2),…,a(n), где a(n) – величина n-го элемента

2. Линейные системы с постоянными параметрами (лпп).

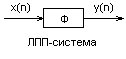
Дискретная система с входной x(n) и выходной y(n) последовательностями

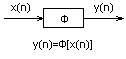
Линейная система:

если x₁(n), x₂(n) входные последовательности,

y₁(n), y₂(n) соответствующие им отклики линейной системы.

При подаче на вход линейной системы входной последовательности ax₁(n)+bx₂(n) на выходе образуется выходная последовательность ay₁(n)+by₂(n), где a и b произвольные постоянные.

Система с постоянными параметрами:

Если x₁(n), соответствует y₁(n),

То x₁(n-n₀), соответствует y₁(n-n₀).

В ЛПП входная и выходная последовательность связана соотношением типа свертки. Пусть h(n) – отклик системы на единичный импульс (импульсная характеристика системы). Тогда входная последовательность:

Поскольку h(n) – отклик системы на последовательность U₀(n), а параметры системы постоянны, то h(n-m) будет откликами на последовательность U₀(n-m). Из свойства линейности следует, что откликом на последовательность x(m)U₀(n-m) должна быть последовательность x(m)h(n-m). Поэтому отклик на x(n) будет равен:

Он имеет вид свертки. Таким образом, h(n) полностью описывает ЛПП систему, что и отражено на рисунке.

3. Разностные уравнения.

Описание ЛПП - системы разностными уравнениями позволяет:

1. найти эффективные способы построения таких систем

2. определить многие характеристики системы (собственные частоты, порядок системы и др.)

Самый общий вид линейного разностного уравнения М-го порядка с постоянными коэффициентами, относящегося к физически реализуемой системе:

где коэффициенты {a_i},{b_i}описывают конкретную систему, причем а_М0.

Уравнение (1) записано в виде, удобном для решения методом прямой подстановки. Имея набор начальных условий [напр. X(i),y(i) для i=-1, -2, …, -M] и входную последовательность X(n), по формуле (1) можно вычислить последовательность y(n) для n0. Например, разностное уравнение y(n) = x(n) – 3y(n-1) с начальными условиями y(-1)=0,x(n)= n²+n можно решить подстановкой:

y(0) = x(0) - 3y(-1) = 0

y(1) = x(1) - 3y(0) = 2

y(2) = x(2) - 3y(1) = 0

y(3) = x(3) - 3y(2) = 12

y(4) = x(4) - 3y(3) = -16

. . .

Существуют методы решения разностных уравнений в явном виде. Основная идея их сводится к получению двух решений р.у.: однородного и частного.

Важное значение р.у. состоит в том, что они непосредственно определяют способ построения цифровой системы.

Пример:

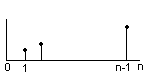
y(n) = - a₁y(n-1) + b₀x(n) + b₁x(n-1)

Его можно реализовать с помощью схемы: