2.2. Понятие об экстремальном управлении

Цель э.у. состоит в обеспечении оптимального статического режима работы объекта. Основной задачей при этом является получение minилиmax Jпри недостаточной информации о характеристиках и условиях работы объекта. За исходную информацию принимается тот факт, чтоJимеет экстремальную зависимость от . При этом неизвестно ни количество экстремумов, ни их положение, ни аналитическое выражениеJ. Система э.у. должна вывести объект на экстремальный режим и обеспечить стабилизацию этого режима. В зависимости от того, является ли экстремальная характеистика стабильной или меняется под влиянием внешних условий, экстремальные системы делят на 2 класса:

1. статические

2. динамические, которые мы и будем рассматривать.

В динамических э.с. возможны два случая:

1. изменения экстремальной характеристики от некоторого параметра известны;

2. изменения экстремальной характеристики от некоторого параметра неизвестныиэ.х. зависит от многих факторов случайным образом.

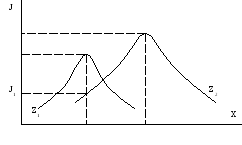
Для примера рассмотрим одномерный объект с экстрем. зависимостью J(x,z)

Пусть J(x,z) имеет переменное экстрем. значениеJ при неизменном значении

В этом случае достаточно каким–либо образом один раз определить положение экстремума , а затем применить обычную систему стабилизацииJпри значении .

Если э.х. одномерного объекта изменяется произвольно как по горизонтали, так и по вертикали, то необходимо применить экстремальное управление, обеспечивающее слежение за экстремумом. Допустим, при Z₁поддерживался режим с . В результате возмущающих воздействий Z₂ э.х. изменилась и . Для экстремального управления необходимо определить новое положение , при котором .

В зависимости от способа поиска экстремума xэ.с. делят на системы:

1. с определением производной для точки .

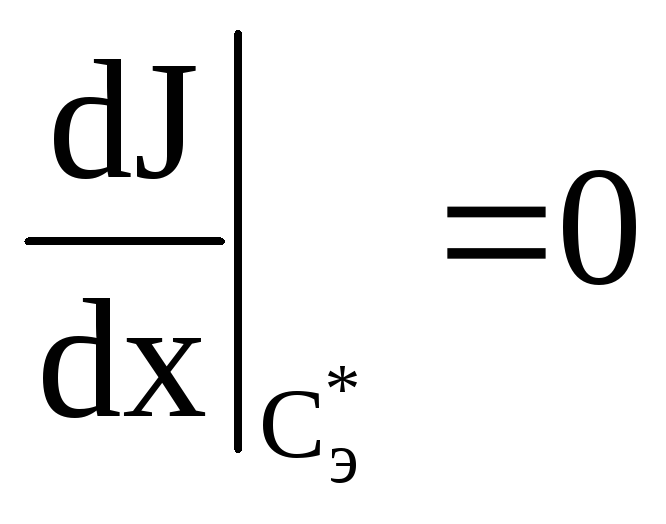2. с определением знака призводной, в точке экстремума меняет знак.

3. шаговые системы, принцип действия которых основан на том, что через определенные интервалы времени измеряются J₁ и J₂, которые запоминаются в ЗУ₁ и ЗУ₂, сравнивниваются и в зависимости от их изменения производится реверс управляющего сигнала x.

4. системы с запоминанием экстремума, для определения с^*используют ЗУ, которое реагирует только на увеличение сигналаJ. До тех пор, покаmax не достигнут сигнал с увеличивается, при достиженииJ_max, сигнал с начинает уменьшаться, увеличиваяJ_max.Процесс этот периодически повторяется.

Существуют и другие способы поиска экстремумов, а значит и другие разновидности э.с.

Работа системы экстремального управления представлениа на структурной схеме

Здесь W₁(p) иW₂(p) – передаточные функции регулятора и объекта управления. Работа системы реализуется по замкнутому принципу. Текущее состояние объекта x(t) оценивается в блоке 1 с помощью значения показателя качестваJ. Блок 2 по значениюJвырабатывает очередное значение , которое не обязательно будет оптимальным. Блок 3 формирует сигнал на перестройку регулятора, в результате которой изменяется его передаточная функцияW₁(p). Сигнал управления будет изменен, изменится соответственно и состояние объекта. Этот процесс будет осуществляется до тех пор, пока , .