Уравнение Эйлера .

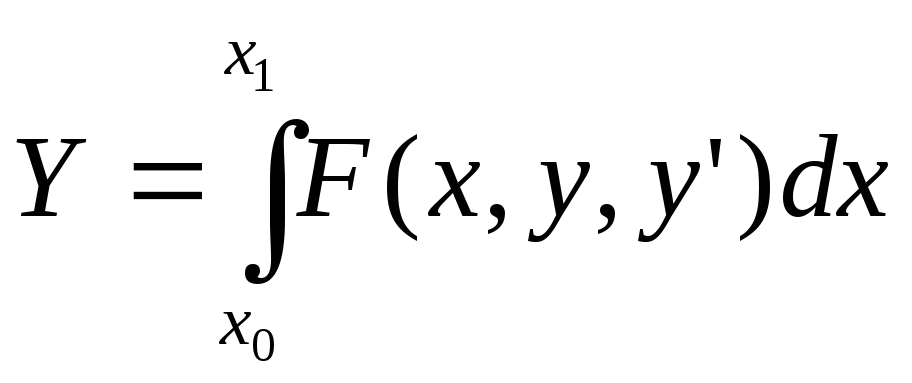
Будем считать F(x) непрерывной вместе с её производными до второго порядка в некоторой области В плоскостиXYи при любыхy^’. Если фиксируемy=y(x), то функционалJполучает фиксированное значение :y(x₀)=y₀,y(x₁)=y₁.

C₁– класс функций, имеющих первую производную.

ε – окрестность кривой y=y(x) ε , иногда добавляют: ε , где ε – близость порядка.

Функционал Jотносительного экстремума дляии удовлетворяет условиям:y(x₀)=y₀,y(x₁)=y₁. Если величинаJдляy(x) не меньше его величины для других, находящихся в ε – близости иy(x₀)=y₀,y(x₁)=y₁.

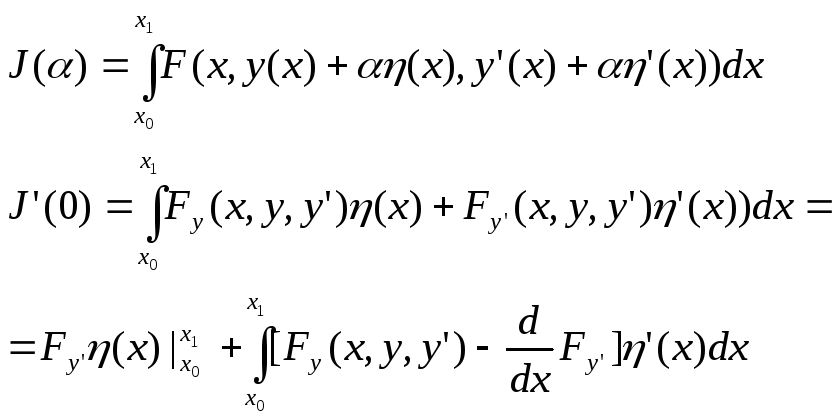
Применяя Лемму будем иметь:

Раскрывая полную производную по xбудем иметь:

- уравнение второго порядка, общий интеграл которого содержит две произвольные постоянные, которые определяются из условий: y(x₀)=y₀,y(x₁)=y₁.

Если

Вариационная задача с ограничением.

Введём соответствия в обозначения: x→ty→xy’→x’

приx(t)φ(t)

В классическом вариационном исчислении считалось, что x(t)- экстремаль,x(t)+δxx(t)-δx– вариации.

Для замкнутой области вывод уравнения Эйлера требует уточнения.

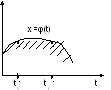
Экстремум можно искать обычным способом:

Или окончательного

- уравнение Эйлера для исходного функционала. Экстремум функционала при наличии ограничения может достигаться на экстремалях, составленных из кусков кривых, удовлетворяющих условию Эйлера и ограничениям. Для полного решения нужно найти условия перехода к дугам на границах и обратно.

Пусть экстремум функционала – достигается на траектории (кривой), составленной из нескольких дуг. Пусть в т.tпроисходит переход экстремали на границу

- вариация внутри области варьирования.

- вариация на границе области варьирования.

т.к.

Теорема Лагранжа о среднем

, где a < c < b

Если то

Условие может нарушаться лишь при =0

Постоянные интегрирования:

1. 2 const– начальная и конечная точки траектории

2. 2 const– точка излома

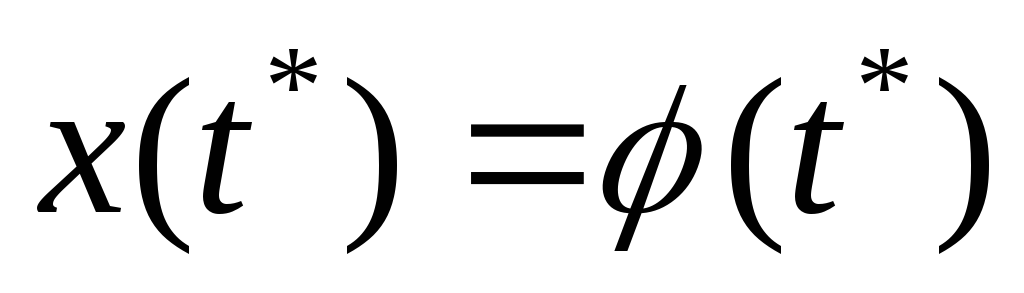
3. 2 const– производная в точке излома

Основная вариационная задача

Пример: ,;,,

EMBED Equation.3

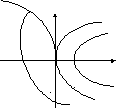
_{u=1 x2}

+1

x₁

u=+1

Ограничения характеристик состояния системы

,(1)

,

ω₂ Пусть задано некоторое управление.

1 Подставив в уравнениенайдем движение

0 системы из в

и заканчивая изменения

ω₁

Нормальный вид ограничений

Нелинейные преобразования характеристик. Тригонометрические преобразования.

Для распространения методов классического вариационного исчисления расширим размерность задачи, введя дополнительные уравнения

Пример1.;;;

Пример2. ;;

Пример3. ;;;

Приведение задач неклассического типа к классическому типу вариационных задач.

Пусть ,,

Состояние системы в момент можно представить изображающей точкой в замкнутой областиΝ+Μ– мерного пространства. Границы замкнутой областиопределяютсяLуравнениями состояния.

,,,

,

Введем дополнительные управления , которые обеспечат выполнение условий.

Математическая модель дополнительной системы: ,.

Пусть выбраны и интегрированием определены, которые соответствуют дифференциальным уравнениям и ограничениям. Дополнительная система содержитΝ+Μ+Lпеременных, подчиненных модели дополнительной системы, в которой проблема односторонней вариации отсутствует.

Необходимые условия экстремума функционала в основной вариационной задаче.

- начальные положения

- конечные положения

- условия связи краевых координат

Найти в классе кусочно-непрерывных функций управления и в классе кусочно-непрерывных функций координатыудовлетворяющих в интервалеуравнениямf,g,ψ, которые сообщают интегралуJэкстремальные значения.