Рассмотрим систему

, где

Теорема: Линейная система с постоянными параметрами является устойчивой в смысле Ляпунова тогда и только тогда, когда

А) все характеристические числа А имеют неположительные действительные части.

Б) любому характеристическому числу на мнимой оси кратности mточно соответствуетmсобственных векторов матрицы А.

Теорема: Динамическая система с постоянными параметрами является асимптотически устойчивой тогда и только тогда, когда все характеристические числа матрицы А имеют строго отрицательные действительные части.

Например:

1.Смесительный бак.

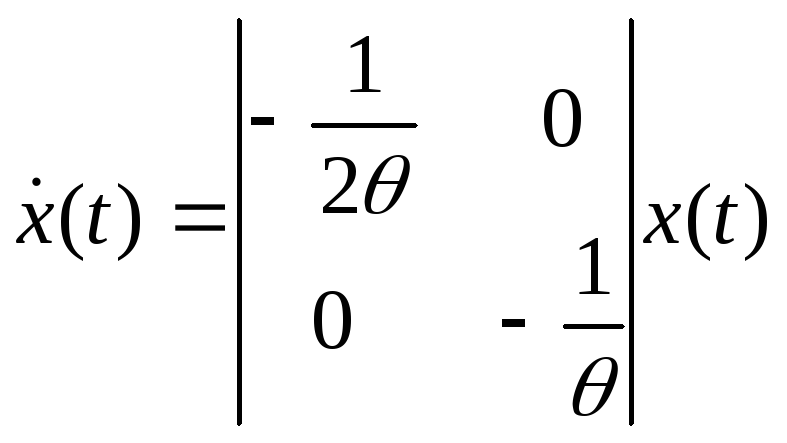: x₁(t)=x₁(0)e, x₂(t)=x₂(0)e

2. Перевернутый маятник

,

Подпространства устойчивых и неустойчивых состояний

Пусть k={1m}=M,J=M+J-M

m-количество характеристических чисел матрицы А с неотрицательной действительной частью матрицы А

n-m- количество характеристических чисел с отрицательными корнями.

Тогда подпространство R_mR_nбудет подпространством неустойчивых состояний

Управляемость.Определение управляемости.

Постановка задачи: определение свойств динамической системы (функции ее параметров), при которых осуществим перевод системы из произвольного состояния x(0) в произвольное состояние,.

Определение : линейная динамическая система будет полностью управляемой , если ее можно перевести из х(0) в х(1) за время.

новое конечное состояние.

Теорема. Линейная динамическая система полностью управляема, если она может быть переведена из начала координат в состояние х(1) за конечное время ().

Пример: смесительный бак имеет равные входные концентрации. Приращение концентрацииСв этом случае неуправляемо.

Теорема: Линейная динамическая система полностью управляема, если матрица Р=(В, АВ, А²В, …, А^n-1В) порождаетn-мерное пространство.

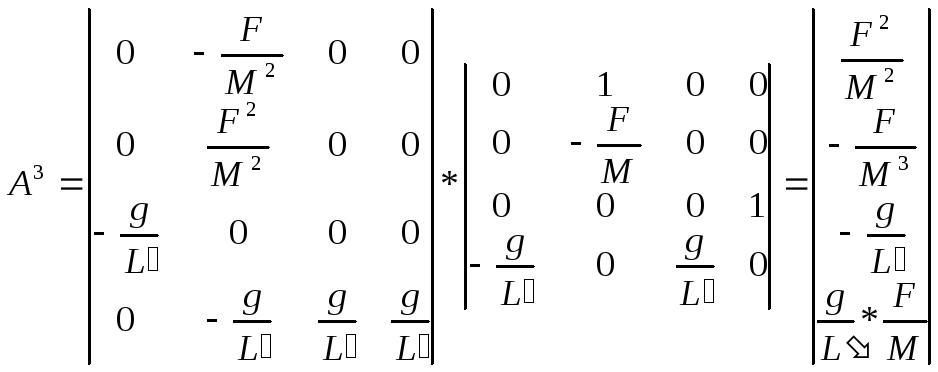
В последовательности матриц В, АВ, А²В должна появиться матрица А^lВ=В₀+АВ₁+…+А^д-1В_lи далее А^l+1В=АВ₀+АВ₁+…+А^lВ_l. Вектор-столбцы матрицы А^lВ линейно зависят от вектор-столбцов матрицы В АВ А²В …А^l-1В.

х(t₁)-принадлежит линейному подпространству, порожденному вектор-столбцами АВ.

Если эти вектор-столбцы не порождают n-мерное пространство можно достичь только состояний меньшей размерности, поэтому система не является полностью управляемой. Если система полностью управляема, вектор-столбцы матрицы Р порождаютn-мерное пространство.

Положим, что Р порождает n-мерное пространство. Тогда выбравu(t) в коэффициентах, можно получить,что любому вектору

будет удовлетворять указанное равенство

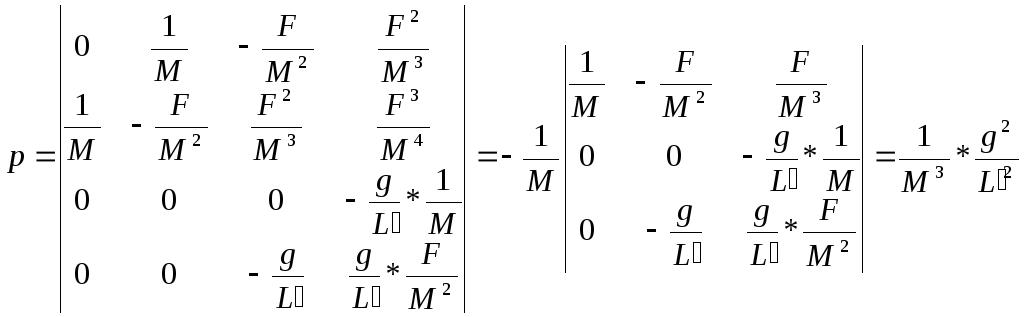
Подпространство управляемых состояний.

Лемма. Если вектор х принадлежит подпространству управляемых состояний, то вектор Ах также принадлежит этому подпространству

Теорема. Линейная динамическая система переходит из состояния х₀в состояние х₁, принадлежащих пространству управляемых состояний, за конечное времяt₁

х₀- принадлежит пространству управления.

- принадлежит пространству упрвления на основании свойства инвариантности

- принадлежит , т.к х₁и е^A(t1-)тоже принадлежит.

Формула показывает, что система переводится из нулевого состояния в за конечное время, что тоже самое из х₀в х₁.

Пусть rank P=m.

е_m– линейно-независимые столбцы управления

Т₁=(е₁…е_m), T₂=(e_m+1…e_n).

Введем

U₂T₁=0

T₁состоит из е₁…е_mпорождающих пространство управляемых состояний, следовательно,U₂x=0.

T_1, АТ₁– принадлежит пространству управляемых состояний

U₂AT₁=0

B– часть матрицы управляемости и принадлежит пространству управляемых состояний

U₂B=0

- каноническая форма управляемости

-матрицаm*m

-полностью управляемая пара. Поведение системы-полностью независимо.

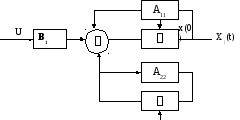
С

X₂(0)

месительный бак

если С₁=С₂=С, то С₀=С

Наблюдаемость.

Пусть y(t,t₀,x₀,u) является выходной функцией линейной динамической системы изменяющейся от начального состоянияx(t₀). Система называется полностью наблюдаемой, если для всехt_iсуществует такой моментt₀, где -<t₀<t₁, что из равенстваy(t,t₀,x₀,u)=y(t,t₀,x₀,u),t₀tt₁ , для всехu(t)t₀tt₁ следуетx₀=x_0.

Теорема:

Система y=Cx, является полностью восстанавливаемой в том и только в том случае, если для всехt_i существует такой моментt₀ -<t₀ <t₁, что из равенстваy(t,t₀,x₀,0)=0t₀tt₁следуетx₀=0

СФ(t,t₀)x₀=CФ(t,t₀)x₀ , x₀=x₀, СФ(t,t₀)(x₀-x₀)=0

Наблюдаемость означает, что имеется возможность определения состояния в момент t₀ по будущим значениям выходной переменной.

Линейная динамическая системаполностью наблюдаема (восстанавливаема), еслиrankматрицы

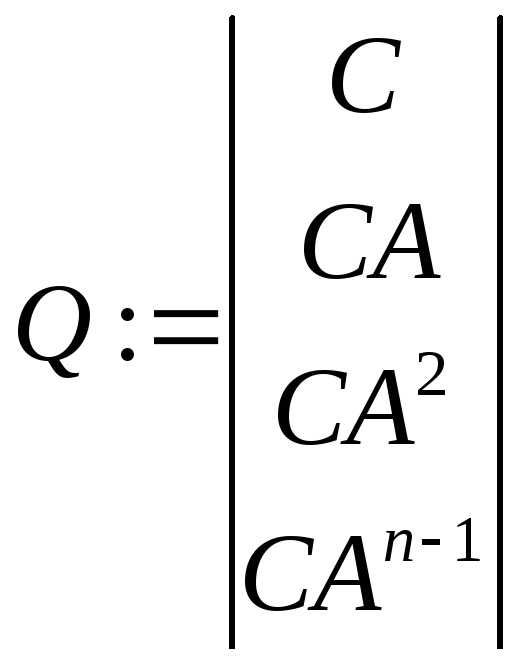равенn.

Если матрица Qне имеет полного ранга, то существует такоеx₀,что:

Сx₀=0 CAx₀=0 ….. CA^(n-1) x₀=0.

Используя теорему Кели-Гамильтона, получим СА^Lx₀=0, гдеLn.

Докажем другое утверждение теоремы:

y(t₀)=Cx₀=0 илиQx₀=0

y(t₀)=CАx₀=0

…………………...

y^(n-1)(t₀)=CA^(n-1) x₀=0

Если Qне имеет полногоранга, то равенства не будет.

Пример:

Rank=2.

Критерий устойчивости линейных динамических систем.

Постановка задачи: рассмотрение фундаментального решения динамической системыпоказало его устойчивость, если действительные части характеристических чисел матрицы А отрицательны.

Определение (прямое) характеристических чисел-процесс трудоёмкий, но не безнадёжный.

Возникает задача: определение отрицательности характеристических чисел матрицы А по самим коэффициентам матрицы А.

Предварительные замечания.

Рассмотрим характеристическое уравнение: .

Введём вектор р=jи рассмотрим 2 случая:

1. Имеем вектор _i=j-p_i, гдеp_i=-+j.

И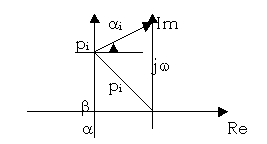зменим векторjот -jдо +j.

Arg_j=-j _i=-/2, Arg_i=

Arg_j=+j _i=/2.

2.Имеем вектор _i=j-p_i , p_i=+j, Arg _j=-j _i=3/2, Arg _j=j _i=/2, Arg_i=-

Рассмотрим D(j)=Mod D(j)e ^jArgD(j)

Теорема:

Изменение аргумента D(j) при возрастанииот -доравно разности между числом (n-m) корней уравненияD(j)=0, лежащих в левой и правой полуплоскостях, умноженной на, т.е.(n-m)-m.

Критерий устойчивости Михайлова:

Если все корни отрицательны, то р_i :Reр_i<0argD(j)=n

D(j)=u()+jv(), гдеu()=а₀–а₂²+а₄⁴-…..

v()=а₁–а₃³+а₅⁵-…..

Так как u()- функция четная, аv()-функция нечетная, тоD(j)=-D(j), т.е. годографD(j) симметричен относительно действительной оси.

Cистема автоматического управления устойчива, если при возрастанииот 0 довекторD(j) повернётся на уголn/2, гдеn-степень полиномаD(j)=0 или его годограф обходит последовательно в положительном направленииnквадрантов.

Система находится на границе устойчивости, если характеристическая кривая проходит через начало координат.

Критерий устойчивости Раусса-Гурвица.

Основное соотношение, определяющее устойчивость Arg_0<<D(j)=n

u()=(а₀ⁿ–а₂^n-2+а₄^n-4-...+ а_n)

v()=(а₁^n-1–а₃^n-3+а₅⁵-…+а_n-1),D(j)=а_ip^n-1.

Для того, чтобы система D(j) была устойчивой, необходимо и достаточно, чтобы все главные определители определителю Гурвица были положительны.

Частотный критерий устойчивости Найквиста-Михайлова.

И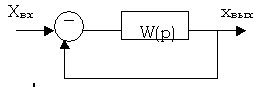меем систему

Введём функцию

D(j)=D_p(j)+M_p(j)

Arg_0<<D(j)=(n-2m)/2

Arg (j)=Arg D(j)-Arg D_p(j)=(n-2m)/2-n/2=-m.

С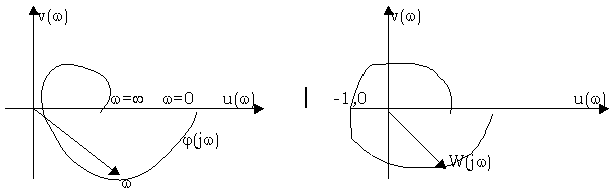истема будет устойчива, если изменение аргументаArg(j)=0, т.е. если годограф характеристики(j) не охватывает начало координат.

Но W(j)=(j)-1, т.е. замкнутая система устойчива, если частотная характеристика разомкнутой системы не охватывает точку (–1,0) при изменении 0<<.

Если разомкнутая система неустойчива, то argD_p(j)=(n-2p)/2

Если замкнутая система устойчива, то arg(j)=argD(j)-D_p(j)=n

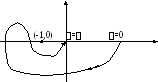Замкнутая система будет устойчива, если частотная характеристика неустойчивой разомкнутой системы охватывает т.-1,0 в положительном направлении Р₁/2 раз, где Р – число неустойчивых корней.

Запас по амплитуде и запас по фазе.

- запас по фазе

20lg(1-A) – запас по амплитуде при проектировании не менее 6 дб.

D-разбиение пространства параметров

Комплексное пространство, мнимая ось которого разделяет его на два полупространства: слева устойчивое, справа – неустойчивое.

D(p)=D_p(p)+M_p(p) – характеристическое уравнение или детерминант возвратной матрицы.

УсловиеD(p)=0= - является функциональной зависимостью фиксирующей какое-то распределение корней и параметров. Если взять и указанную неявную зависимость сделать явной относительно любого параметра , то зависимость будет при р=jпредставлять преобразование пространстваjвU()+jV()=a_jи в том же числе мнимую осьj. Пусть преобразование может быть представлено как на рисунке, т.е. однолистная область преобразована в многолистную. Как правило, областью устойчивости является пересечение областей.

V(j)

U(j)

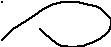
Пример: p³+p²+p+a₀=0

a₀=-p³-p²-p  a₀=²+j(²-1)

U()=² V()=(²-1) 0<a₀<1

Анализ устойчивости одноконтурных динамических систем методом логарифмических АФЧХ.

Анализ устойчивости построен на критерии Найквиста-Михайлова.

A()=20lg

-

1).Для устойчивости замкнутой системы, у которой частотная характеристика разомкнутой системы первого рода, необходимо и достаточно, чтобы ¹_ср<⁰_cр.

2). Для устойчивости системы в замкнутом состоянии необходимо и достаточно, чтобы разность между числом положительных и отрицательных переходов() через -равнялась 0.

lg()

lg()

()

L()

Метод корневого годографа.

Совокупность точек р_i, удовлетворяющих уравнениюN_p(p)+kM_p(p)=0 при различныхk_iназывают корневым годографом.

1. При к0 полюсы замкнутой системы стремятся к полюсам разомкнутой системы.

2. При кполюсы замкнутой системыnстремятся к нулямmразомкнутой системы и (n-m) к бесконечности.

3. Число асимптот (n-m) определят их углы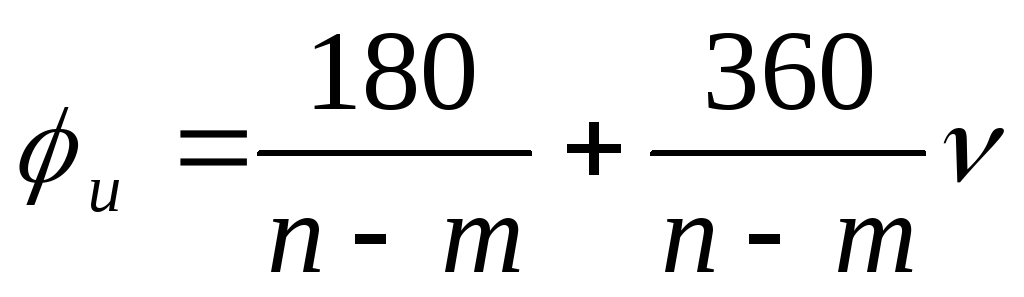(1)=(0.1…n-m-1). Все асимптоты пересекаются в одной точке (2)

1. следует из

2. 

4. Участки годографа на оси абсцисс определяются действительными нулями и полюсами.

_k=+

5. Точки отхода годографа от действительной оси определяются следующим образом:

(,0) – координаты точки отхода

(,) – координаты корневого годографа, близкого к оси абсцисс

6. Точки пересечения годографа с мнимой осью определяются U()=0V()=0, позволит определитьи к.

7. Углы выхода годографа из комплексных полюсов и их подходы к комплексным нулям определяются выражением: для близкой точки.

8. На корневом годографе различают параметр к. Корневой годограф – траектория движения корней в комплексной плоскости р, полученные с помощью уравнений замкнутой системы.

Пример:

D(p)=p³+3p²+2p+2k,p₁=0,p₂=1,p₃=-2

S₀=

, ₁=-0.422, ₂=-1.58

U()=-3²+2k=0, =

V()=j(2-³)=0, k=3

Метод Д-разбиения.

к

Анализ линейных САУ. Основные компоненты систем управления.

Выход

1. объект управления

2. датчик

3. регулятор

4. Задача управления или условие функционирования

Пример:

1)саморегулируемая система отопления дома.

2)спутниковая телевизионная антенна.

Общие формализованные черты:

1. Поведение – система дифференциальных уравнений или модель М.

2. Математический аппарат для анализа и синтеза получил название решающих процедур Т.

3. Исходные данные и ограничения А и С.

4. Проектное решение и его оценка RиK.

5. Обратная связь и возмущения.

6. Задание.

Задачи регулирования и слежения.

Переменные:

1. U(t)-управление

2. V_p(t)-возмущение

3. y(t)-наблюдение

4. V_m(t)-шум измерения

5. z(t)-управляемая величина

6. r(t)-задание или эталонная переменная

z(t)r(t)tt₀-задача.

В исходных данных на проектирование необходимо учитывать:

1. неконтролируемость действующих на объект возмущений

2. недостоверность или переменность параметров объектов

3. неизвестность начального состояния

4. наблюдаемая переменная искажена шумом и не несет инфомации о регулируемой величине.

Разомкнутая система: управление основано только на прошлых и текущих значениях эталонной переменной.

Пример системы управления.

Замкнутые регуляторы могут накапливать информацию об объекте, его начальном состоянии уменьшать влияние возмущений и компенсировать неопределенность параметров.

Проектирование замкнутых систем.

Дифференциальные уравнения объекта .

Наблюдаемая переменная .

Управляемая переменная .

Дифференциальное уравнение регулятора.

Критерии качества работы:

Среднеее значение квадрата ошибки слежения Се(t) и среднее значение входной переменной Сu(t) определяется выражениями:

и – заданные неотрицательно определенные симметричные весовые матрицы в частном случае диагональные.

Основной принцип проектирования:

При проектировании следует добиваться минимума и .

1.Сначала вычисляют

и

2.Затем вычисляют

3.

Введем обозначения:

Подставим , где -постоянная или средняя часть входного воздействия.

-переменная или вариабельная часть.

Матрица повариационных плотностей энергии

процесса

Например экспоненциального корректирования шума

Квадратичные формы.

Допущения:

1. Система управления ассимптотически устойчива.

2. Система управления имеет постоянные параметры и постоянные матрицы и

3. и

В случае многомерной векторной системы имеем:

Одномерная система управления

Входная величина и выходная (управляемая) переменная скалярные.

Принимаем

Для минимизации нужно придерживатьсь следующих принципов.

Определение: Для минимизации малого установивщегося значения средне квадратичной ошибки слежения передаточная функция линейной системы с постоянными параметрами следует выбирать таким образом, чтобы выражение принимало минимальное значение для всех действительных . В частности если заданные точки нулевые .

Общий подход: Разделить диапазон частот: там, где значительное нужно иметь минимальное и наоборот.

Полоса частот , где . Полоса частот – интервал .

Если то называется частотой среза. При =0,01 определяют как 1% частоту среза.

Определение: Пусть rскалярный процесс со спектральной плотностью энергии . Полоса частот определяется как и содержит заданную часть половины энергии процесса .

Если , то говорят об 1% частоте среза, что означает содержание в интервале 99% от половины энергии процесса.

Д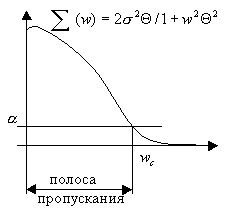ля получения малого(квадрата ошибки) необходимого чтобы полоса пропускания частот системы содержала как можно большую часть полосы пропускания системы.

Рассмотрим

Для получения малого нужно иметь в полосе частот эталонной переменной.

Следцет отметить что это не означает что малая величина, т.к. этот член определяет постоянную часть эталонной переменной, т.е от заданной рабочей точки во входной переменной. Второй член важен для динамического диапазона входной переменной и поскольку этот диапазон ограничен, то входная величина должна быть ограничена тоже.

Однако принципы проектирования и - противоречивы. Систему можно спроектировать так, чтобы удовлетворялся один из принципов.

Выберем :

Если при то это означает, что при должно увеличиваться, а это означает, что остается большим в частотном диапазоне входного сигнала . Это приводит к перегрузке системы.

Задача синтеза регулятора, основаная на частотных методах.

Порядок решения:

1. Составляют математическое описание объекта.

2. Выбирают регулирующий орган и силовой привод, усилитель и датчики.

3. Составляют передаточные функции и строят ЛАФЧХ и ФЧХ.

4. По заданным требованиям на частотные характеристики строят желаемые частотные характеристики ЛАФЧХ и ФЧХ.

5. По построенным желаемым и действительным частотным характеристикам определяют тип и место введения корректирующих устройств.

Корректирующие устройства бывают последовательные, параллельные и комбинированные.

Последовательные корректирующие устройства достаточно просты, но их включение всегда приводит к увеличению частоты среза и следовательно полосы пропускания системы при , т.е. когда .

При этом приходится применять более быстодействующие приводы и большим потреблением мощности.

Параллельные корректирующие устройства более сложные, но они сужают полосу пропускания.

В сложных системах применяют как пораллельные, так и последовательные методы.

Выбор характеристик двигателя.

Зависимость массы и номинальной выходной мощности.

Выбор механической передачи

-момент инерции ротора

момент инерции якоря двигателя .

Синтез последовательных и параллельных корректирующих устройств.

Синтез параллельного устройства