Переходная матрица

- уравнение состояния.

Теорема 1.Для однородного уравнения, гдеА– постоянная величина, для всехtвсегда существует решение,.

Переходная матрица является решением матричного дифференциального уравнения:

для всехt..

Теорема 2.Переходная матрицалинейной дифференциальной системы имеет следующие свойства:

1) ,;

2) - неособая для всех;

3)

4) - сопряженная система.

Доказательство.

Теорема 3.Для линейного неоднородного дифференциального уравнениягдеB(t) иu(t) – кусочно-непрерывные функции, решение имеет вид

Рассмотрим систему с выходной переменной y=Cx.

Если , то

импульсная переходная функция.

Экспонента от

или

Почему использовали термин “ Экспонента от ”?

4. Решение уравнения приимеет вид:

Далее эвристически покажем, что можно рассматривать как бесконечный ряд

1. При

2. При почленном дифференцировании имеем:

Устойчивость линейных систем с постоянными параметрами

Рассмотрим где). Система устойчива, если малые отклонения от положения равновесия, т.е. решенияостаются малыми при сколь угодно большом увеличении времени и наоборот система неустойчива, если малые отклонения становятся сколь угодно большими.

Определение

Системаустойчива, если евклидова нормаостается ограниченной при, т.е. для любогоисуществует, такое что, тодля.

Решение является асимптотически или абсолютно устойчивой, если

Решение является экспоненциально устойчивым, если

Устойчивость линейных систем с постоянными параметрами

где- собственные векторы,– скаляры, определяемые через.

Линейная система является устойчивой в смысле Ляпунова тогда и только тогда, когда все характеристические числа матрицыАимеют неположительные действительные части, и любому характеристическому числу на мнимой оси кратностиmточно соответствуетmсобственных векторов матрицыА.

Задачи операционного исчисления.

Операционное исчисление Лапласа.

Оригинал и изображение.

Оригинал – любая функциядействительного аргументаt, удовлетворяющая условиям:

а) кусочно - непрерывности за исключением конечного числа точек разрыва первого рода;

б)

в) существуют ,такие, что для всехt

Изображение:

или

Пример.

, при.

Пример.

Пример.

Теорема:Изображение оригиналаопределено в полуплоскости, где– показатель роста оригинала.

Действительная и мнимая части изображения

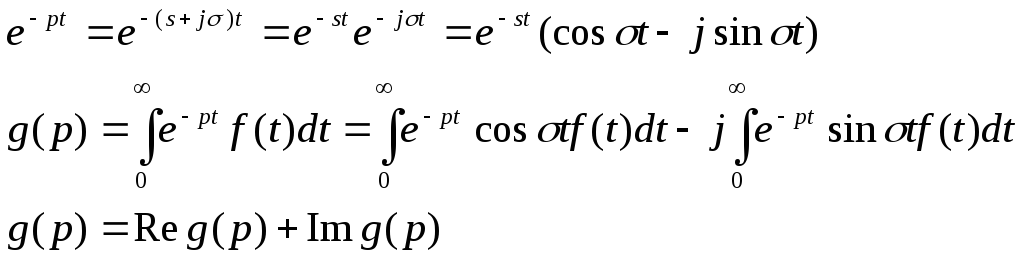
Простейшие свойства преобразования Лапласа

Линейность: ;=>

Подобие: ито

Запаздывание:

Пример

Система с постоянными параметрами является асимптотически устойчивой тогда и только тогда, когда все характерные числа матрицы А имеют строго отрицательные действительные части.

Дифференцирование оригинала

Интегрирование оригинала

Формула обращения

Изображение ;

Корни знаменателя , являющиеся полюсами дробно-рационального изображения,Сутьс кратностями. Если ,, то

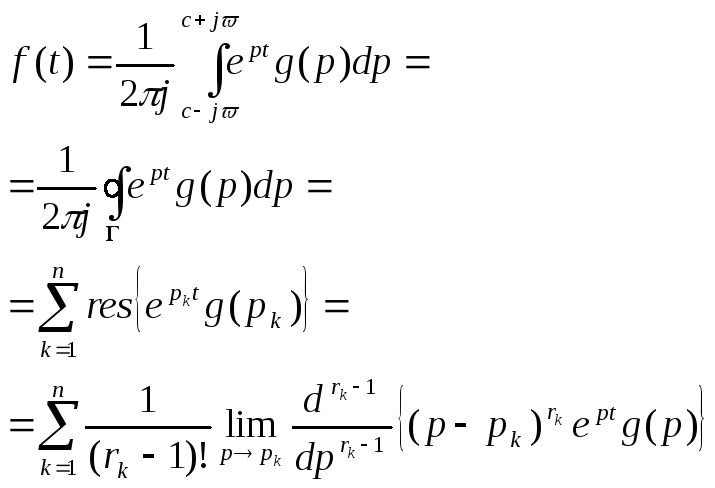
Теорема:если изображениеявляется дробно-рациональной функцией со степенью числителя меньше степени знаменателя, имеющего корникратности, то оригинал определяется следующим (см. выше) образом.

Следствие: Если, где корни простые, то

Пример 1:

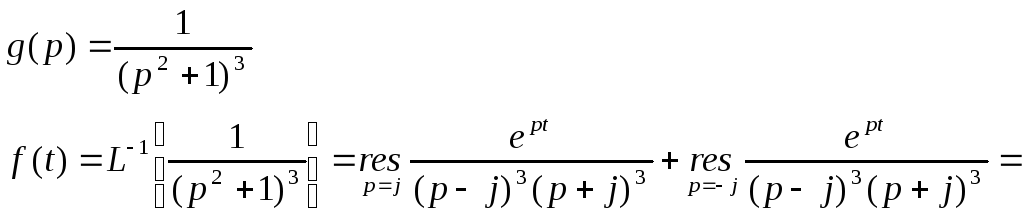
Пример 2:

Анализ систем с постоянными параметрами на основе преобразования Лапласа

Решение дифференциального уравнения состояния.

Теорема:Пусть матрица системыАявляется постоянной матрицей размерноститогдаилигдерезольвента матрицыА.

Рассмотрим постоянную матрицу А, размерности с характеристическим полиномомтогдагде

Пусть тогдаприимеемилигде- матричная передаточная функция системы.

Пример 1.

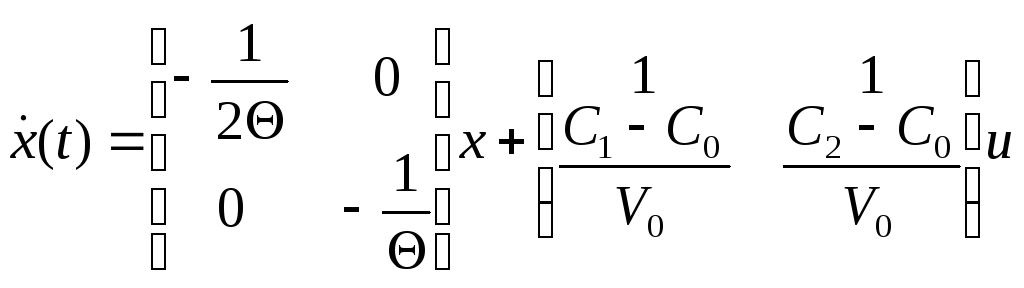
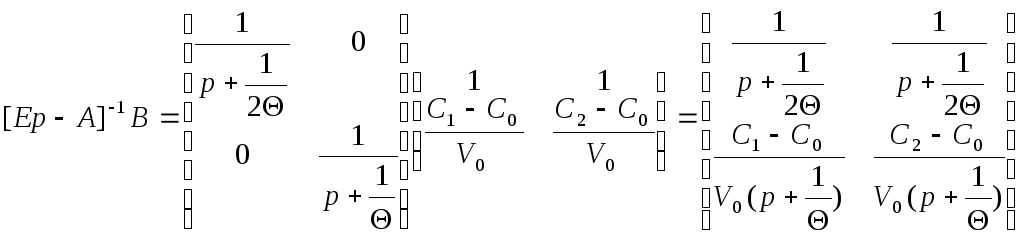
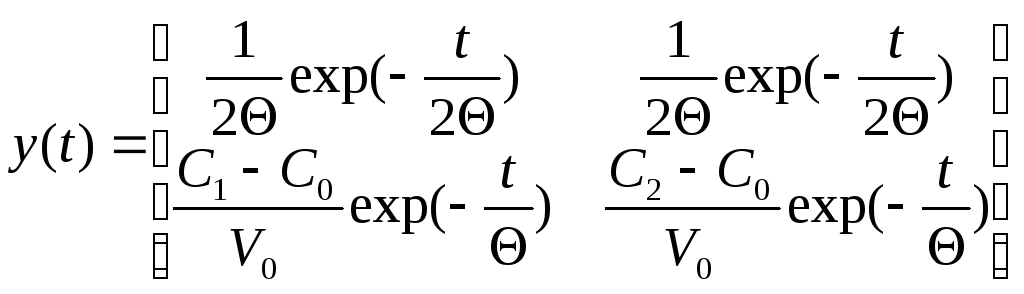
Теорема о конечном значении

Теорема о наименьшем значении

Соединения линейных систем

Введем расширенный вектор состояния

Если ,

то

(1)(2)

Cистема (1) не имеет прямой связки, что позволяет избежать неявных алгебраических уравнений.

– матрица возвратной разности

- матрица усиления контура

Статические и астатические системы

r-y₂– ошибки системы управления.

при условии, что

Система является статической, т.е. имеет ошибку в установившемся состоянии, если числитель и знаменатель функции имеют свободные члены не зависимые отp.

Если же функция имеет нуль какого-либо порядка приp=0, то система является астатической первого порядка.

Система имеет астатизм порядка , если передаточная функция имеет нуль порядка.

Пусть

Типовые звенья систем автоматического регулирования

Передаточная функция

Каждый полином (числитель и знаменатель) может быть представлен в виде разложения на простые множители

Амплитудная частотная характеристика

Логарифмическая амплитудно-частотная характеристика

Асимптотические логарифмические характеристики

Наклон

Ошибка

Колебательное звено

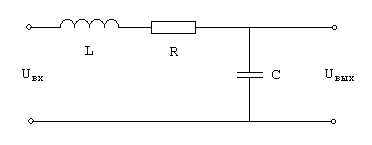
LC=T² RC=2T

Частотная характеристика

=₀

Корни характеристического уравнения

Если =0, то=0=1/T=₀

Логарифмическая характеристика

Lg 

40 дб/дек

1)

2)

Интегрирующее звено

U_вх=Ri, ,

V()

-/2

Дифференцирующее звено

W(p)=Tp

W(j), h(t)=T(t)

Форсирующее звено первого порядка

W(p)=Tp+1

W(j)=jT+1

Усилительное звено

W(j)=k,L()=k

Устойчивость. Определение устойчивости.

Задача: Рассмотрение поведения дифференциальных уравнений на длительном интервале времени.

Пусть уравнение состояния имеет вид .

Исследовать будем приu(t)=0,x₀(t) – номинальное решение

Определение: Пусть - дифференциальное уравнение с номинальным решением. Номинальное решение устойчиво по Ляпунову, еслиt₀и>0 существует(,t₀)>0 такое, чтоx(t₀)-x₀(t₀)<,x(t)-x₀(t)<t>t₀, )<,x(t)=

Определение: номинальное решение x₀(t) уравнения состоянияx(t) является асимптотически устойчивым, если

А) оно устойчиво по Ляпунову

Б) t₀существует(t₀)>0 такое, что приx(t₀)-x₀(t₀)<(t₀)

Определение: Номинальное решение x₀(t) уравнения состоянияявляется асимптотически устойчивой в целом (большом), если оно

А) устойчиво по Ляпунову

Б) для любого и t₀x(t)-x₀(t)0 приt

Три условия (случая):

1. Ограниченность начального отклонения Ограниченность дальнейшего отклонения.

2. Ограниченность начального отклонения сходимость к 0 дальнейшего отклонения (устойчивость в малом).

3. Неограниченность начального отклонения сходимость к 0 дальнейшего отклонения (устойчивость в большом).

Для нелинейных систем устойчивость решений, а для линейных -устойчивость систем, т.к. если и , то.

Определение: линейная динамическая система устойчива в определенном смысле (по Ляпунову, асимптотически как в малом так и большом), если травиальное решение устойчиво в этом смысле x₀(t)0.

Теорема. Линейная динамическая система асимптотически устойчива тогда и только тогда, когда она асимптотически устойчива в целом.

Теорема следует из безусловной продолжаемости решений.

Теорема: линейная динамическая система с переменными параметрами является экспоненциально устойчивой, если существуют положительные константыитакие, чтоt>t₀.

Устойчивость линейных систем с постоянными параметрами.