Теорема о начальном значении.

Теорема о конечном значении.

Передаточные функции.

Заметим, что – не являетсяz-преобразованием, соответствующим, хотя=.

Передаточные функции:

Φ*(z)=- по выходному сигналу;

Φ_ε*(z) =- по ошибке;

С помощью этих передаточных функций выходной сигнал и сигнал ошибки в дискретные моменты времени могут быть вычислены по формулам:

Если выражения разложить в ряд по z^-n , то получимX(nT) и, соответственно,E(nT).

Для нахождения сигнала в любой момент времени необходимо ввести запаздывание.

Дифференцирующий цифровой фильтр.

Частотные характеристики непрерывного и цифрового дифференциаторов.

Если требуется более точное дифференцирование, то необходимо использовать более точную формулу:

Цифровые интеграторы.

Впростейшем случае :

Можно осуществить более точное численное интегрирование:

Сравнение двух методов показывает, что:

1. объём памяти одинаков;

2. во втором случае больше на одну операцию суммирования.

Устойчивость дискретных следящих систем.

Определение устойчивости.

Дискретную систему будем называть устойчивой, если при ограниченном входном сигнале выходной сигнал также ограничен.

Если g(iT)<M , то x(iT)<M₁

Для дискретной системы необходимым и достаточным условием устойчивости является ограниченность суммы для всех σ:

- достаточность

Для устойчивости дискретной следящей системы необходимо и достаточно, чтобы все корни знаменателя передаточной функции были расположены внутри единичного круга.

Алгебраический критерий устойчивости Шур-Кона.

В теории полиномов существует критерий отсутствия корней по модулю больших единицы.

Если все детерминанты отличны от нуля, то этот полином не имеет нулей на окружности иNего нулей расположены вне этой окружности, причёмNравно числу перемен знаков в последовательности: 1, Δ₁, Δ₂…, Δ_n.

Пример:, если n=2, a₀=1, a₁=A, a₂=И

Частотные критерии устойчивости.

Пусть игде,.

Для устойчивости дискретных систем достаточно, чтобы годограф знаменателя передаточной функции замкнутой системы охватывал начало координат nраз, гдеn- степень полинома. Разность между степенью полинома и числом оборотов годографа вокруг начала координат даёт порядок неустойчивости, т. е. число

Для определения устойчивости замкнутой системы по годографу устойчивой разомкнутой системы достаточно, чтобы годограф передаточной функции разомкнутой системы не охватывал точку (-1,j₀).

Число оборотов годографа вокруг этой точки равен порядку неустойчивости системы, т. е. числу корней k, .

1. Годограф любой системы начинается на действительной оси :

2. ЕслиY*(z) имеет полюсz=1:

при

Если φ изменяется отдо, тоY*(z) описывает окружность бесконечно большого радиуса изменяясь отдо. Если при этом охватывает точку (-1,j₀), то система не устойчива.

Пример:

Раскроем неравенства:

1. 

2. 

3. 

Первые два условия выполняются при k>0 всегда (отр. обр. связь). Третье условие – ограничение по величине коэффициента усиленияk:

______________

Оптимальное уравнение.

Задача дифференциального исчисления – отыскание экстремумов функций:

Задача вариационного исчисления:

Ответ: функция f(x) – должна удовлетворять определённому дифференциальному уравнению.

Лемма1:

Если 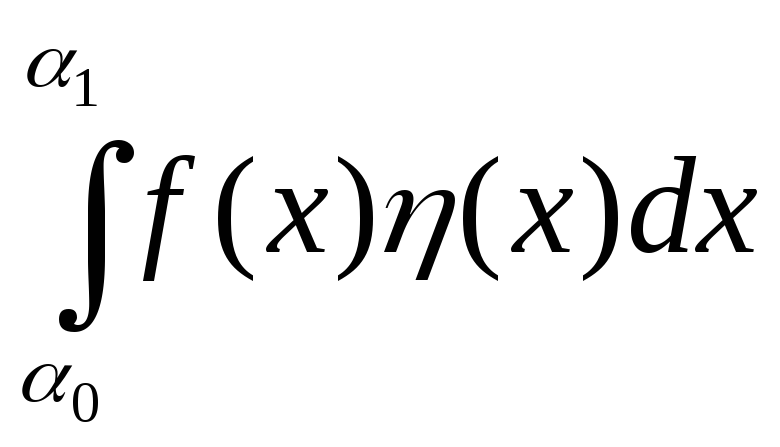, гдеf(x) – фиксированная непрерывная в промежутке [x₀,x₁] функция, обращается в нуль для всякой функции η(x) непрерывной вместе со своей производной и равна нулю на концах: η(x₀)= η(x₁)=0, тоf(x) –тождественно равна нулю в промежутке [x₀,x₁].

Доказательство:

Пусть _, тогдаx:x=z f(ε)>0. Вследствие непрерывностиf(x) будет положительной на отрезке [ε₁,ε₂]:

Определим η(x):

что противоречит условиям теоремы.

Лемма2:

Если , гдеf(x,y) – фиксированная в области В непрерывная функция, обращается в нуль для всякой η(x,y) непрерывной вместе со своими частными производными первого порядка в В и равной нулю на контуреLв области В , тоf(x) – тождественно равна нулю в области В. Положим, чтоf(x,y)=f(ε,ξ)>0. Тогда она положительна в некотором круге радиуса ρ с центром (ε,ξ).

η(x,y)=