Замкнутая импульсная система

Ошибка системы

- может иметь разрывы в момент квантования .

При определении решетчатой функции следует оговорить

или .

Будем считать предел справа, т.к. импульсный элемент формирует именно правое значение.

Полагая , окончательно находим:

.

Для определения нужно это уравнение решить, что возможно, например, с помощью дискретного преобразования Лапласа.

Уравнение импульсных многомерных систем

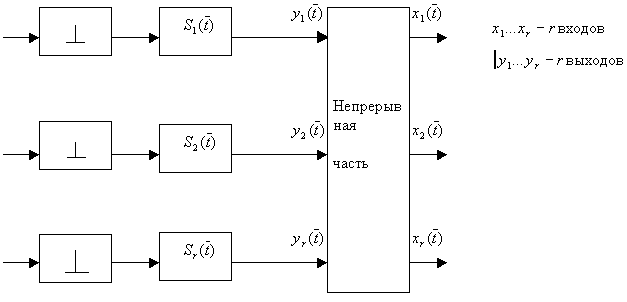
Все импульсные элементы работают синхронно и синфазно.

,

Пусть - фундаментальная матрица.

, приx(0)=0

, .

Матрица , при

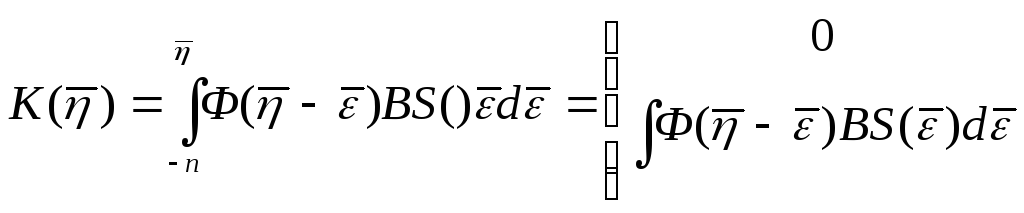
Тогда уравнение импульсной системы можно представить как

или полагая

-уравнение ошибки

Z - преобразование. Определение и условие существования.

Z-преобразование рассматривается применительно к сигналу с импульсной модуляцией.

при <0,

<– условие достаточное, но не необходимое. Если выбрать значенияg(t) приt=nT, то существует , гдеz=e

Это выражение с точностью до множителя Tявляется полной аналогией непрерывного преобразования.

, так какdt=T, аnT=t, поэтому дискретное преобразование Лапласа называют ещё обобщённым преобразованием.

Пример: ,

Геометрическая прогрессия: a_n=a₁q^n-1;S_n=;

-z-преобразование для непрерывной функции.

-z-преобразование для непрерывной функции с запаздыванием.

В более общем виде условия существования z-преобразования для дискретной функции,, гдеn<0.

Нетрудно доказать сходимость ряда: Рассмотрим ряд, представляющий геометрическую прогрессию со знаменателем, которая сходится приq<1 илии его сумма равна . Но каждый член , где=R=e^cT– радиус сходимости.

Связь z-преобразования с преобразованием Лапласа.

- аналитическая дискретная функция.

- дельта Функция.

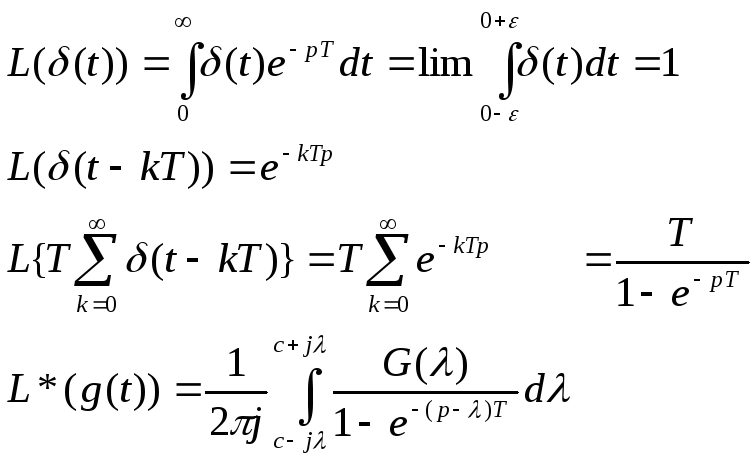
Эта формула устанавливает связь между преобразованием Лапласа для непрерывной функции и соответствующим z-преобразованием.

Прямая интегрирования должна лежать правее полюсов G(λ) и левее. Равенство справедливо приRep>c₀– абсцисса абсолютной сходимости.

Вычислим интеграл с помощью вычетов.

Полюсы подынтегральной функции внутри контура интегрирования будут совпадать с ,;z=e^pT

С помощью этой формулы удобно определить z-преобразование по известному преобразованию Лапласа непрерывной функции.

Определение оригинала по известному z-преобразованию.

g(kT)

Если k>nиi>n, то в этой формуле всеb_iприi>nиa_kпропадут:

Эти формулы позволяют, не производя каждый раз деления, определять дискретные значения функции оригинала для дробно-линейных преобразований z. Формулы очень удобны для вычислений и могут быть использованы для вычисления переходных процессов в непрерывных системах.

Теорема Котельникова.

Устанавливает эквивалентность непрерывного и дискретного сигналов.

Точная формулировка теоремы применима к непрерывным сигналам со спектром, ограниченным по частоте.

Допустим, что имеем непрерывный сигнал g(t), спектр которогоG(ω) равен нулю при

В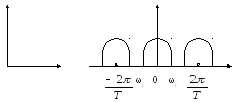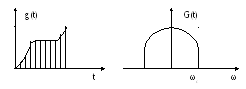озможны 3 случая:

1.

2.

3.

при

Определение и свойства преобразования с запаздыванием.

При σ→0 z-преобразование переходит в обычноеz-преобразование.

1.

2.

3.

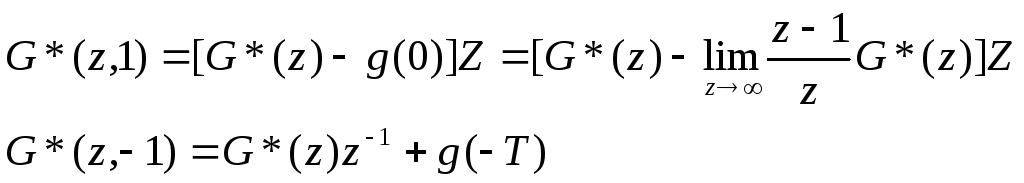
Определения и свойства w-преобразования.

z=e^pT – замена

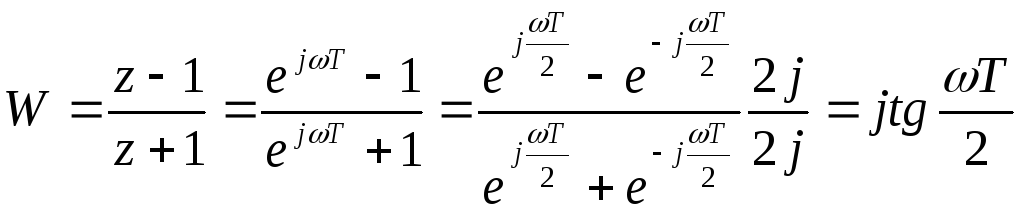
wz+w=z-1w+1=z(1-w) и тогдаe^-at

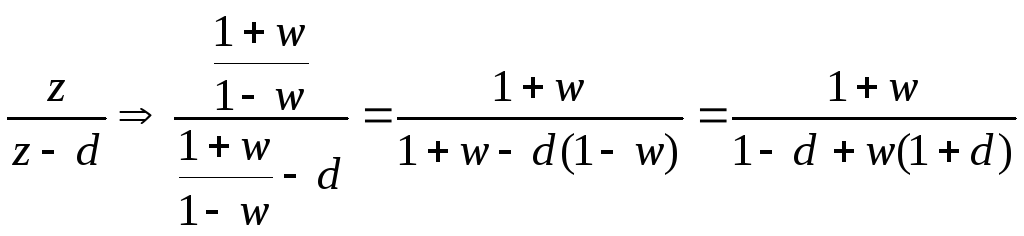
Некоторые теоремы z-преобразования.

Теорема линейности.