Решение уравнения разности к определяется наиболее просто если уравнение разрешимо относительно функции .

Зададим к начальных условий при

Используя вычислим последовательно и все остальные значения при . Пологая , вычисляем при , т.е ,

т.е.

или

Решение является общим в том же смысле как решение линейного дифференциального уравнения.

Наряду с разностным уравнением относительно решетчатых функций можно рассматривать уравнение относительно смещенных решотчатых фцнкций

Линейные разностные уравнения

1. - неоднородное разностное уравнение.

Будем считать, что функции определены при и ограничены.

Уравнение 1 можно преобразовать к виду

где

Коэффициент без ограничения общности можно считать равным 1, а

Теорема 1.Если решетчатые функции являются решениями линейного однородного уравнения то функции где производные постоянные также являются его решениями.

Теорема 2.Если решетчатые функции линейно-зависимы,то при всех значениях ,при которых они определены обращаются в ноль.

Теорема 3.Если решетчатые функции линейно независимые решения однородного разностного уравнения при и не обращается в ноль ни при одном , то определитель не обращается в ноль ни при одном .

Линейные неоднородные разностные уравнения.

Общее решение линейного неоднородного разностного уравнения равно сумме частного решения и общего решения однородного уравнения

где – произвольная постоянные, а -решения однородного уравнения для которого

Доказательство:

если -решение неоднородных уравнений, то , тогда - однородное уравнение, а его решение.

Пример:

:

Решение однородного уравнения

тогда

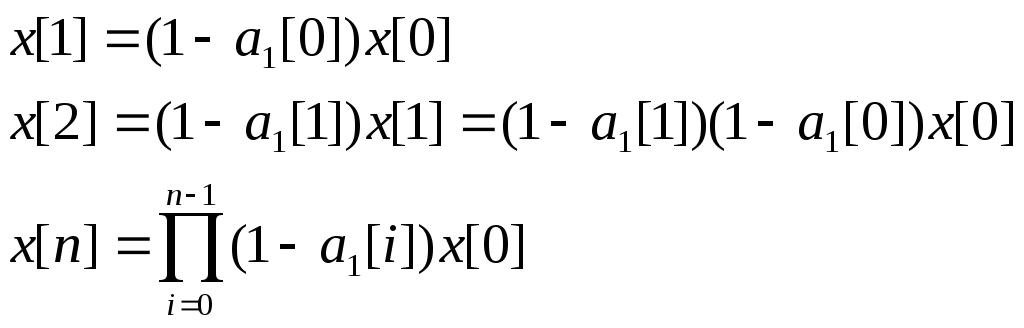
или

Разностные уравнения с постоянными коэффициентами.

Будем искать решение

- хапрактеристическое уравнение разностного уравнения.

Найдем корни - характеристического уравнения.

Если корни простые, то - ре6шения разностного уравнения.

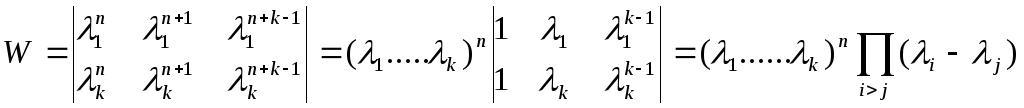
Если корни различны, то определитель не равен нулю и решетчатые функции независимы и решение имеет вид:

Если и - сопряженные комплексные корни

и - сопряженные комплексные константы

Системы разностных уравнений

Система разностных уравнений связывает решетчатые функции и их разности вплоть до порядков соответственно

Переходя к разности будем иметь:

Линейноя система разностных уравнений:

Уравнение импульсных систем автоматического регулирования

Системы автоматического управления в которых применяются импульсная модуляция называются импульсными системами автоматического управления.

А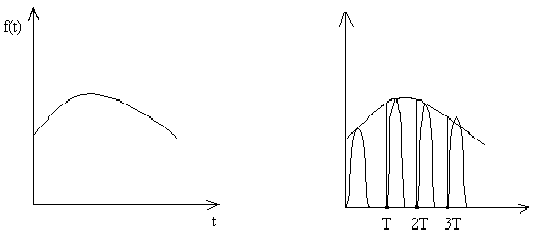мплитудно импульсная модуляция – замена непрерывного сигнала последовательностью импульсов с постоянным интервалом времени Т.

Пусть - функция описывающая форму импульса, тогда

У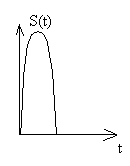стройство, в котором осуществляется модуляция называют импульсными элементами.

Одномерная импульсная система:

Н.Э – импульсный элемент

Н.Ч – непрерывная часть

З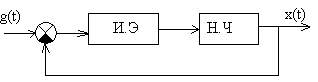амкнутая импульсная система:

М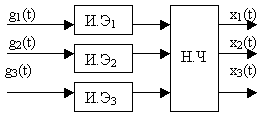ногомерная импульсная система:

Синхронная система– система с совпадающими периодами импульсов.

Синфазная система– синхронная система, у которой совпадают моменты возникновения импульсов.

Составление уравнений импульсных систем:

1. Описание дифференциальными уравнениями.

2. Описание интегральным преобразованием:

В дальнейшем, полагая будем иметь

Для описания импульсных систем применяют два вида уравнений:

1. Описание с помощью разностных уравнений

2. 

Уравнения импульсной системы с одним импульсным элементом:

- импульсное описание непрерывное части.

- описание импульсного элемента.

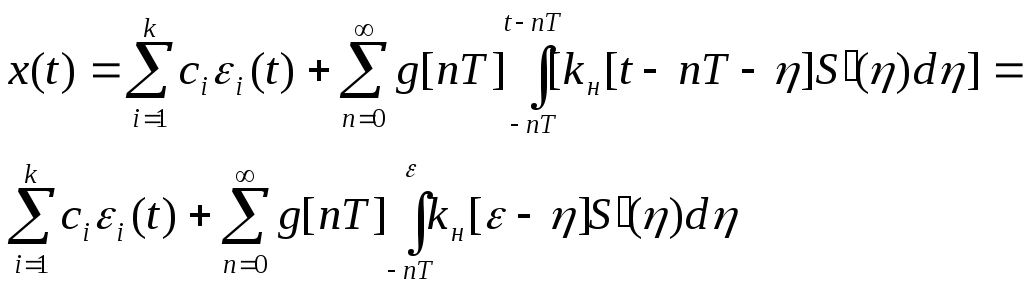
Здесь

Примем во внимание , что , а функция обращается в 0 при т.е. при

Но функция обращается в 0 также при , где - ширина импульса

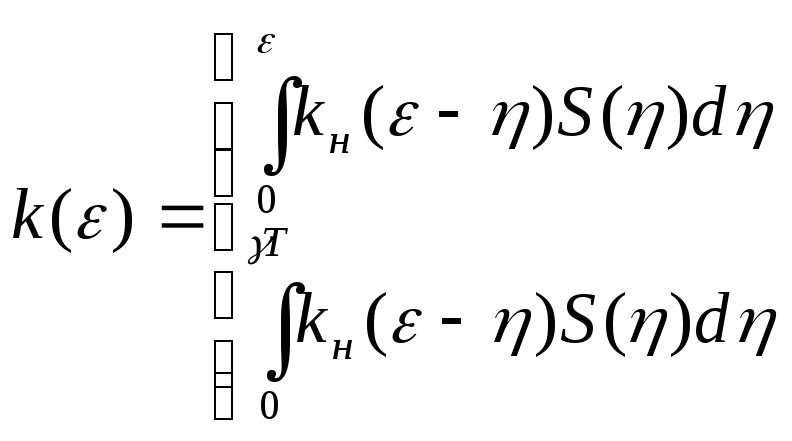
Уравнение разомкнутой импульсной системы можно записать:

Функции можно придать определенный физический смысл, если ввести понятие о простейшем импульсном элементе.

Простейший импульсный элемент описывается

Единичная ступенчатая функция.

Смещенная единичная ступенчатая функция

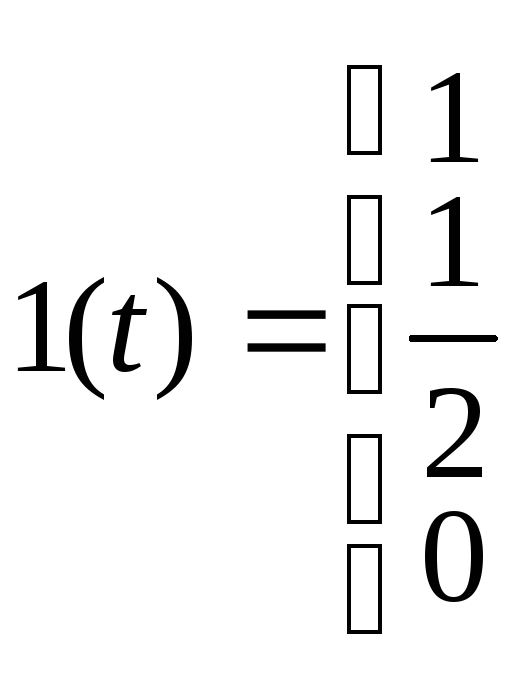
1). 2). 3).

Основное и важное фильтрующее свойство

Это уравнение имеет тот же вид, что и уравнение исходного импульсного элемента, но не может быть воспроизведен никаким реальным устройством.

Реальный импульсный элемент можно представить в вид:

Непрерывный элемент с весовой функцией s(t) называют формирующим элементом.

Простейший Формирующий элемент

импульсный элемент

С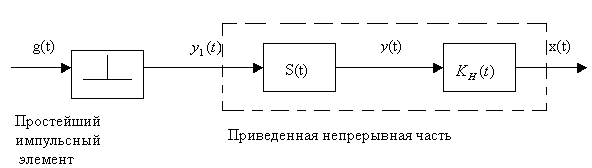труктурная схема разомкнутой импульсной системы

Импульсная система – последовательное соединение простейшего импульсного элемента, формирующего элемента и непрерывной части.

Непрерывная часть + формирующий элемент = приведенная непрерывная часть.

Если продолжительность импульса мала , весовая функция приведенной непрерывной части приближенно может быть заменена весовой функцией непрерывной части у-жимой на постоянных коэффициентах.

Вернемся к уравнению разомкнутой системы :

при нулевых начальных условиях

.

Введем относительное время .

Введем обозначения:

, , .

Выражение импульсной переходной функции

Введем новую переменную

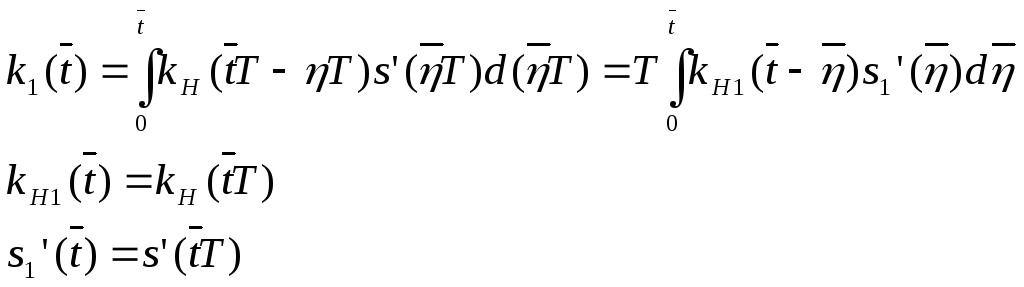
Уравнение равно свертке функций и умноженной наT.

Уравнение разомкнутой импульсной системы можно записать в виде:

Учитывая, что =0 при можно записать:

Пример:

Вход системы:

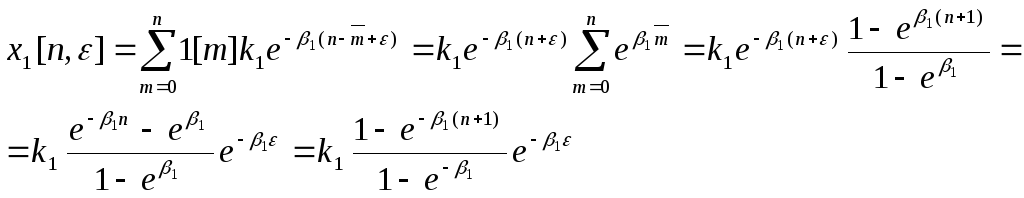
где ,