
- •Литература
- •Введение
- •Основные понятия и определения теории управления
- •Переходная матрица
- •Устойчивость линейных систем с постоянными параметрами
- •Определение
- •Задачи операционного исчисления.
- •Операционное исчисление Лапласа.
- •Простейшие свойства преобразования Лапласа
- •Анализ систем с постоянными параметрами на основе преобразования Лапласа
- •Рассмотрим систему
- •Подпространства устойчивых и неустойчивых состояний
- •Управляемость.Определение управляемости.
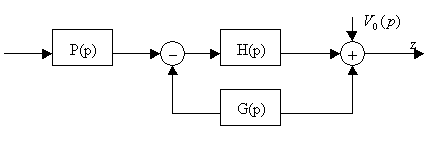
- •Влияние возмущений
- •Влияние шума наблюдения на и
- •Решение уравнения разности к определяется наиболее просто если уравнение разрешимо относительно функции .
- •Линейные разностные уравнения
- •Линейные неоднородные разностные уравнения.
- •Системы разностных уравнений
- •Уравнение импульсных систем автоматического регулирования
- •Замкнутая импульсная система
- •Уравнение импульсных многомерных систем
- •Z - преобразование. Определение и условие существования.
- •Связь z-преобразования с преобразованием Лапласа.
- •Определение оригинала по известному z-преобразованию.
- •Определение и свойства преобразования с запаздыванием.
- •Теорема о начальном значении.
- •Передаточные функции.
- •Цифровые интеграторы.
- •Уравнение Эйлера .
- •Теорема Лагранжа о среднем
- •Основная вариационная задача
- •Ограничения характеристик состояния системы
- •Нормальный вид ограничений
Влияние возмущений
Возмущения, действующие на систему ухудшают показатели качества регулирования.
Исследуем зависимость возрастания квадрата ошибки слежения и квадрата входной переменной за счет действия возмущений и сформулируем принципы проектирования.
Примем допущения:
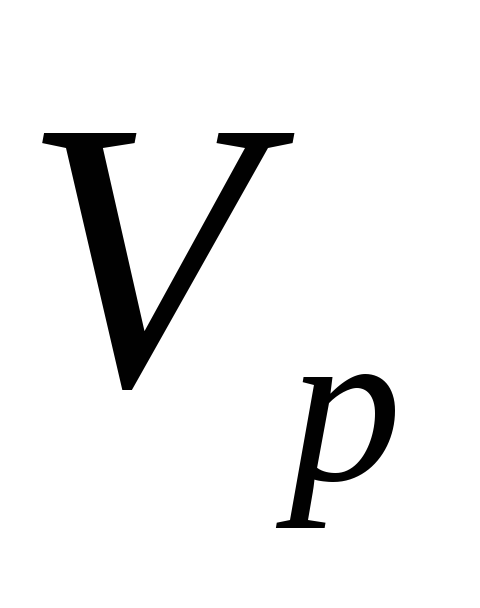 -процесс
не корректированный с
-процесс
не корректированный с
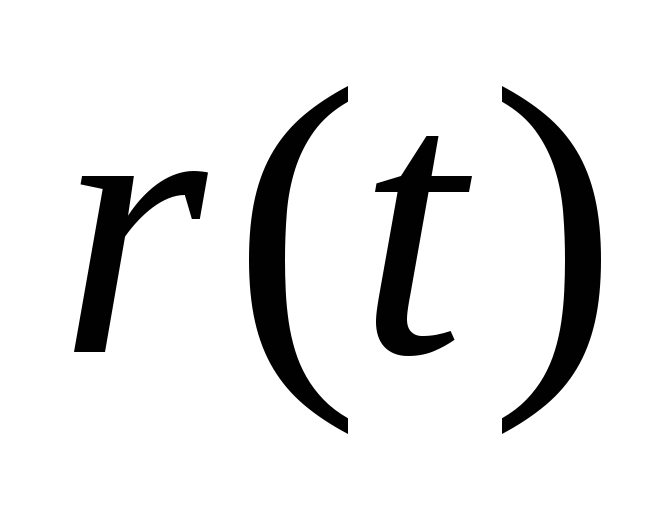 и
и
 .
.Управляемая переменная является наблядаемой
 ,
,
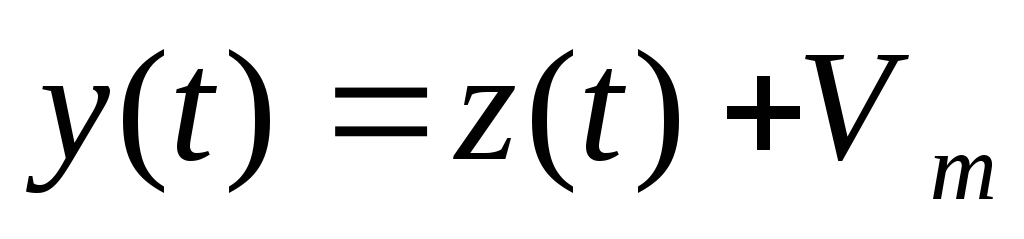 .
.Система управления является ассимптотически устойчивой.
Входная и управляемая переменная является скалярными и
 и
и
 .
.
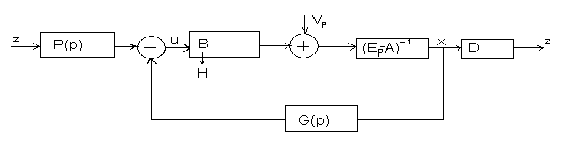
![]() :
:
![]()
![]()
![]()
![]()
![]() –
неособая матрица.
–
неособая матрица.
Составляющая от постоянной части
возмущений в установившемся среднем
значении квадрата ошибки слежения :
![]() ,
,
![]() , где
, где
![]() -
момент второго порядка от
-
момент второго порядка от
![]() .
.
Составляющая от переменной части возмущений :
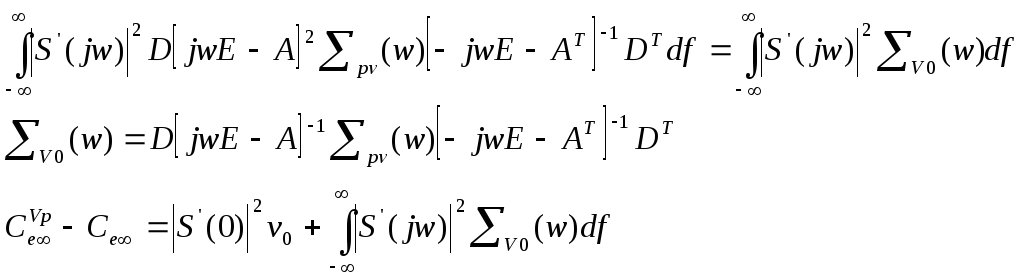
![]() -
среднее значение квадрата ошибки
слежения с возмущением.
-
среднее значение квадрата ошибки
слежения с возмущением.
![]() -
среднее значение квадрата ошибки
слежения без возмущения.
-
среднее значение квадрата ошибки
слежения без возмущения.
![]()
Уменьшение прироста
![]() от возмущения
от возмущения
![]() в асимптотически устойчивой линейной
системе достигается за счет малости
абсолютного значения функции
чувствительности
в асимптотически устойчивой линейной
системе достигается за счет малости
абсолютного значения функции
чувствительности
![]() в полосе частот возмущения.
в полосе частот возмущения.
![]() малое значение
малое значение
![]() - большое значение, что противоречит
условиям устойчивости.
- большое значение, что противоречит
условиям устойчивости.
Среднее значение квадрата входной переменной :
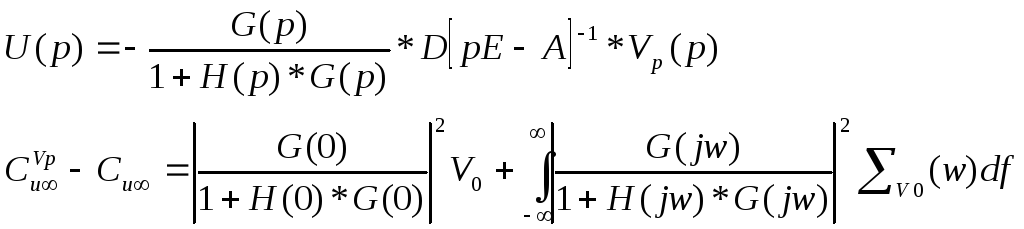

Чтобы получить малое увеличение
![]() необходимо малое значение
необходимо малое значение
![]() в диапазоне частот эквивалентного
возмущения.
в диапазоне частот эквивалентного
возмущения.
Влияние шума наблюдения на и

![]()

Чтобы уменьшить прирост установившегося
среднего значения квадрата ошибки
слежения от шума наблюдения в асимптотически
устойчивой системе необходимо иметь
малой величины
![]() в полосе частот шума наблюдения.
в полосе частот шума наблюдения.
![]()
![]()
Разностные уравнения и импульсные системы
автоматического управления
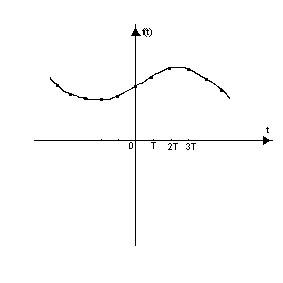
Решетчатые функции:
n– целое число
Т – постоянная (период дискретности)
![]()
Введем время
![]()
Смещенная решетчатая функция.
При фиксированном
![]()
Смещенная решетчатая функция удовлетворяет
условию:
![]() .
.
Если имеем разрыв первого рода в точке
![]() ,
то
,
то
![]()
![]()
В этом случае
![]() ,
т.е.
,
т.е.
![]() .
.
![]() функция
двух аргументов.
функция
двух аргументов.
Конечные разности решетчатых функций
![]() - конечная
разность первого порядка
- конечная
разность первого порядка
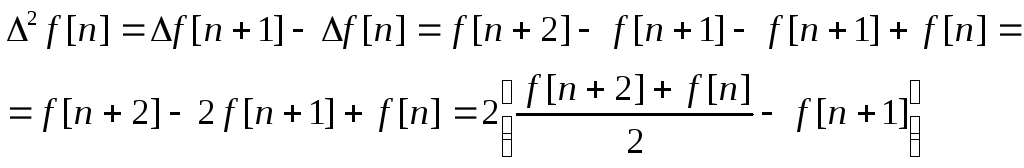
![]() - разность порядка
- разность порядка
![]() .
.
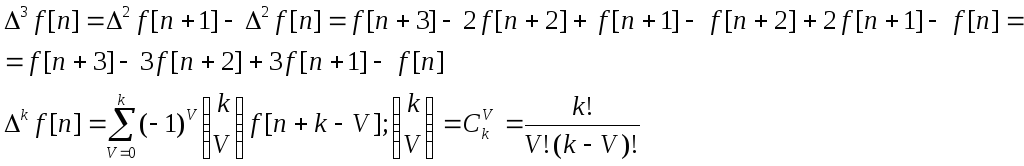
Примеры:
1.
![]()
![]()
2.
![]()
![]()
![]()
3.
![]()
![]()
![]()
![]()
4.
![]()
![]()
![]()
![]()
Линейность операции

Суммирование решетчатых функций
Пусть
![]() -
решетчатая функция.
-
решетчатая функция.
Найти
![]() для которой
для которой
![]() является первой разностью.
является первой разностью.
![]() первообразная
функция.
первообразная
функция.
![]()
Если решетчатая функция определена при
всех целочисленных значениях аргумента
n=0,1,2…,
то
![]() ряд,
который должен сходиться.
ряд,
который должен сходиться.
Если
![]() первообразная
для
первообразная
для
![]() ,
то
,
то
![]() также является первообразной для
также является первообразной для
![]() действительно
действительно
![]() .
.
Общий вид первообразной :![]() .
.
Значение cможно выразить
через значение первообразной при
каком-то фиксированномn=N,
![]() или
или
![]() .
.
Если положить n=N+l:
![]() ,l=[1,2,…]
,l=[1,2,…]
или при N=0:
![]() .
.
Для решетчатых функций справедлива формула суммирования по частям :
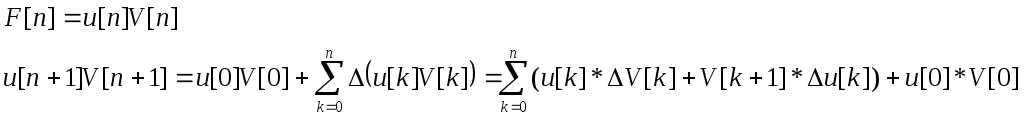
![]() - формула
суммирования по частям
- формула
суммирования по частям
Пример:
![]()
![]() n=[0,1…]
n=[0,1…]
![]() ;
;
Разностные уравнения.
![]()
Разностное уравнение связывает
n-решетчатую функцию
![]() и разности до некоторого порядка или
и разности до некоторого порядка или
![]()
Например:
![]()
![]()
Если исходное уравнение содержит в
явном виде
![]() и
и
![]() ,
то исходное уравнение называется
разностным порядка к.
,
то исходное уравнение называется
разностным порядка к.
Решетная функция
![]() ,
обращающая разностные уравнение в
тождество называется его решением.
,
обращающая разностные уравнение в
тождество называется его решением.
