20. Свертка функций.

Пусть заданы две функции и, определенные на всей действительной оси. Времяtменяется отдо.

(1)

Введем новую функцию, которую назовем сверткой двух функций и.

(2)

Считается это следующим образом:

- свернутая с функцией. Для получения сверткииследует заменить переменнуюtна, затем в функцииаргументзаменить на, то есть образовать, перемножить две функции, а затем взять интеграл.

Основные свойства свертки функций:

1. Свертывание двух функций обладает свойством коммутативности. То есть:

(3)

Доказательство

Докажем, что

Обозначим и запишем:

Свойство коммутативности свертки аналогично свойству коммутативности двух чисел.

2. Свойство ассоциативности.

Если заданы , то справедливо следующее соотношение:

(4)

Введем обозначения:

и

Свойство (4) будет доказано, если будет установлено следующее равенство:

(5)

Подставим в функцию:

Вводим и получаем:

Меняем порядок интегрирования и получаем:

Так как значение интеграла не зависит от наименования переменной интегрирования, то правая часть этого равенство совпадает с правой частью равенства (5).

3) Свойство дистрибутивности.

Заданы 3 функции и, для них справедливо следующее равенство:

(6)

Доказательство

Имеем

Следовательно, формула (6) справедлива. Если ипри, то, когда. И, когда.

Следовательно, , когда.Тогда свертка функций выглядит так:

(7)

21. Определение оригинала по изображению.

(1)

Обратное преобразование Лапласа определяется по формуле (1). Установим однозначное соответствие между изображением и оригиналом в точках непрерывности f(t).

Пусть F(s) является изображением, и пусть, когда, имеет конечное число полюсов.F(s) удовлетворяет условиям леммы Жордана.

Лемма Жордана.

При F(s), стремящейся на дугек нулю приравномерно относительноargsпри любом положительном значенииt, имеем:

(2)

Где - часть окружности с радиусомR, находится в полуплоскости.

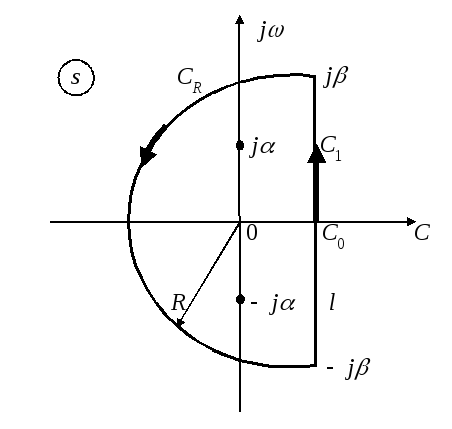
А теперь, применяя теорему о вычете, получаем:

(3)

Так как изображение F(s) является оригиналом, где, то все полюсы находятся на прямой, параллельной мнимой оси и проходящее через точку.

При следует положить, чтоf(t) тождественно равна нулю. Следовательно, присогласно лемме Жордана справедливо:

(4)

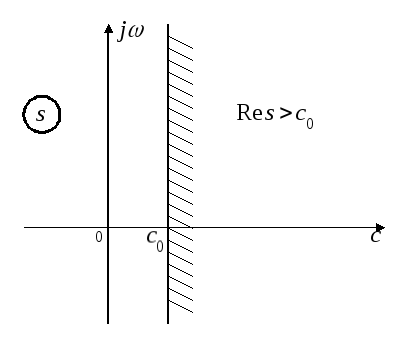
При этом - часть окружностиCс радиусомR, который находится в полуплоскости. Следовательно, присправедливо:

Так как изображение F(s) – аналитическая функция, для которой сумма вычетов равна нулю.

22. Решение линейных дифференциальных уравнений с постоянными коэффициентами с помощью преобразования Лапласа.

Имеется линейное дифференциальное уравнение:

(1)

Заданы начальные условия:

Алгоритм нахождения обыкновенных линейных неоднородных дифференциальных уравнений.

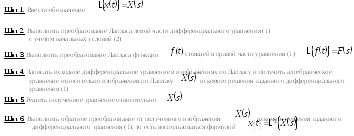
Алгоритм решения дифференциальных уравнений второго порядка.

(2)

23. Прямое и обратное преобразование Фурье.

Совокупность операций, которые позволяют по f(t) найти соответствующую ей спектральную характеристикуназывается преобразованием Фурье.

Преобразование Фурье задается формулой:

(1)

Символически преобразование Фурье будет обозначаться следующим образом:

(2)

Интеграл правой части уравнения (1) понимается как главное значение:

Равенство (1) устанавливает связь между функцией f(t), аргументом которой является действительное числоtи комплексная функция, в качестве аргумента которой играет частота.

Пример

Найти спектральную характеристику . При этоми это действительное число.

Решение

Заданная функция на всей оси времени tкусочно – непрерывна и абсолютно непрерывна, поэтому она преобразуема по Фурье.

Покажем, что интеграл (1) абсолютно и равномерно по отношению к параметру сходится. Для этого надо оценить интеграл по модулю: