4. Системы линейных дифференциальных уравнений с постоянными коэффициентами.

 Линейная однородная система дифференциальных уравнений с постоянными коэффициентами

     В векторной форме:

dY/dx=AY,

где

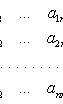
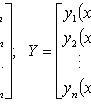
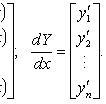
     Характеристическое уравнение

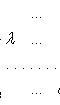
или .

     Нахождение общего решения системы по методу Эйлера

     1. Если - простой корень характеристического уравнения, то ему соответствует решение

числа находятся из системы

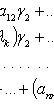
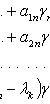
2. Если - корень кратностиmхарактеристического уравнения, то ему соответствует решение вида

где P₁(x),P₂(x), ...,P_n(x)- многочлены степени не вышеm-1, имеющие в совокупностиmпроизвольных постоянных.

     Коэффициенты многочленов можно определить, подставив выражения для y₁,y₂, ...,y_nв исходную систему.

     Найдя решения, соответствующие каждому корню характеристического уравнения, общее решение системы получим как линейную комбинацию этих решений.

     Например, если все корни характеристического уравнения простые, а решениями, соответствующими этим корням , будут:

то общее решение этой системы имеет вид:

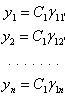
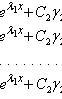
     Линейная неоднородная система дифференциальных уравнений с постоянными коэффициентами

где

     Общее решение неоднородной системы есть сумма общего решения однородной системы и некоторого частного решения неоднородной системы.

     Для нахождения общего решения неоднородной системы можно применить метод Лагранжа вариации произвольных постоянных.

5. Комплексные числа, их геометрическая интерпретация.

Комплексным числом называется выражение вида

(1)

Гдеz– комплексное число,a– действительное число,b– мнимое число. Символj– корень из. Для это символа выполняются следующие равенства:

иназываются равными, если равны их действительные и мнимые части.

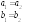
называется сопряженной числуz, если.

М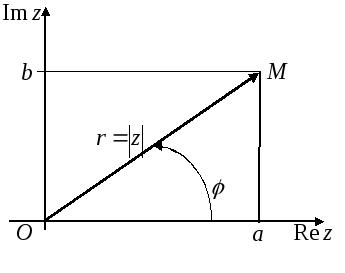одуль и аргумент комплексных чисел.

Расстояние от 0 до M– это модуль комплексного числаr.

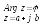
(2)

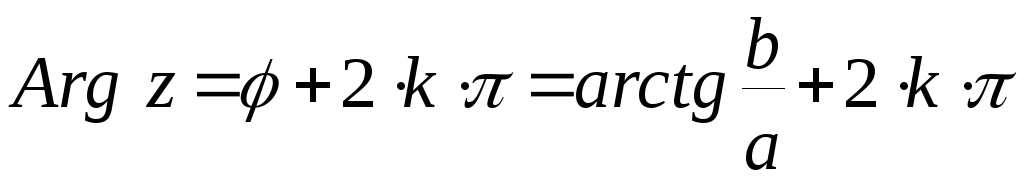
(3)

Изменяется от 0 до .

Если , тои аргумент комплексного числа не определен.

6. Возведение в степень и извлечение корня.

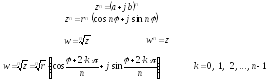
Каков показатель корня, таково и значение комплексного числа.

8. Производная функции комплексного переменного.

Пусть непрерывна в областиz.

В плоскости zрассмотрим две точки,и, каждая точка принадлежит областиz.

Составляется отношение:

Производная поz:

(1)

Для существования производной требуется, чтобы предел (1) существовал и зависел от способа стремления .

Функция f(z) называетсяаналитическойфункцией в областиz, если в каждой точке этой области имеет производные и она не прерывна. Это определение аналогично определению предела действительной переменной и поэтому все свойства сохраняются.

9. Условия Коши-Римана.

Дает условие существования производной в точке.

Для того, чтобы функция , определенная в некоторой окрестности точки , имела производную в этой точке, необходимо и достаточно, чтобы:

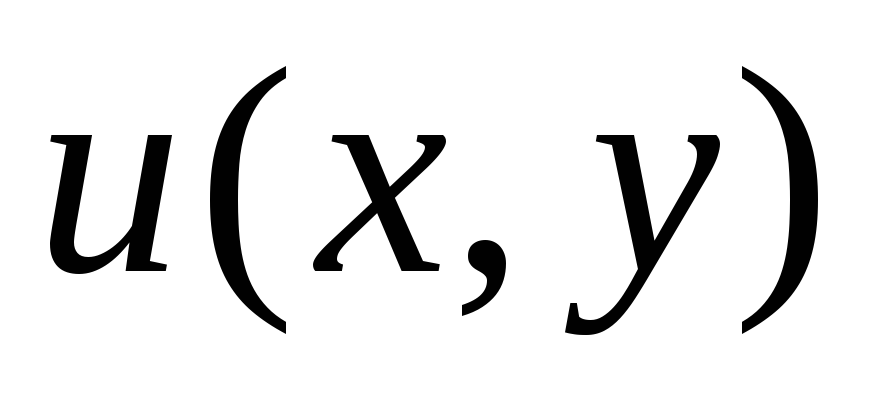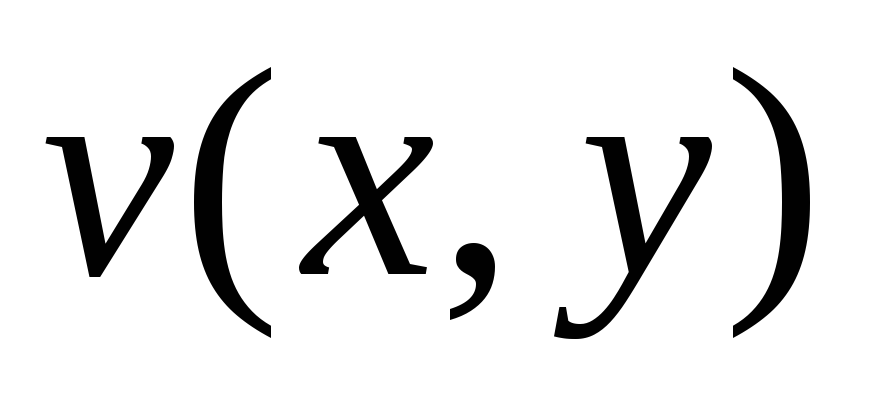1. Функции ибыли дифференцируемы в точке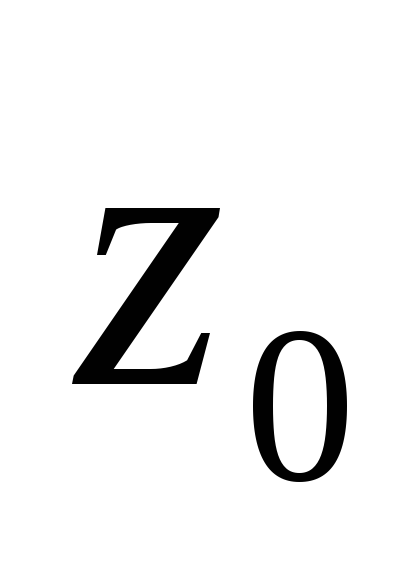поxиy.

2. В точке выполнялись условия Коши – Римана:

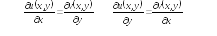
Функция f(z) задана в тригонометрической форме. Это равносильно тому, что заданы две действительные функциии. Тогда условие Коши – Римана формулируется следующим образом:

Для существования производной в точке необходимо и достаточно, чтобы:

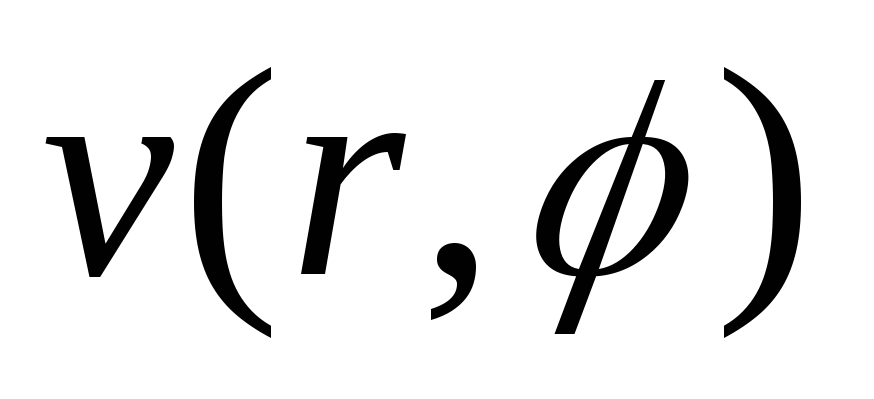1. Функции ибыли дифференцируемы по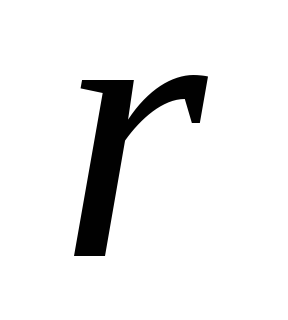и.

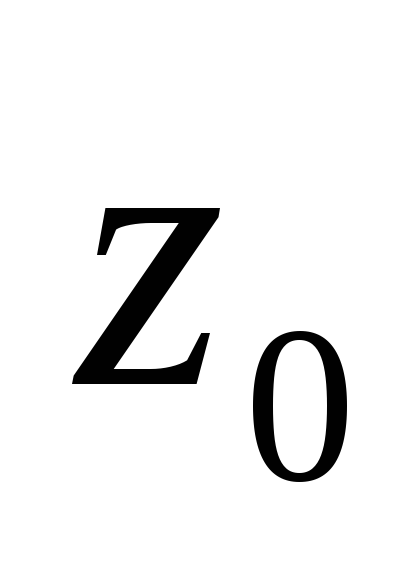2. В точке выполнялись условия Коши-Римана в следующем виде: