13. Формула Коши. Теорема о среднем.

Пусть задана f(z), которая аналитична в областиG, и задан составной контур, который ограничивают некоторую область.

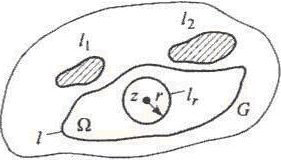
Т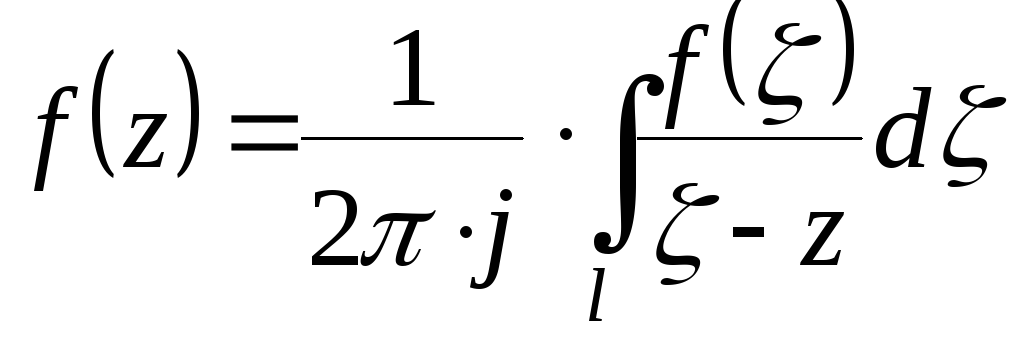огда для любой внутренней точкисправедлива формула:

(1)

Из этой формулы следует, что, зная значение аналитической функции на контуре, можно вычислить значение функции в любой точке, ограниченной этим контуром. Если задать контурв виде окружности с радиусомrв центре точкиz, то справедливо равенство:

иформула (1) принимает вид:

(2)

Формула (2) называется формулой среднего значения. Из нее следует, что задание аналитической функции f(z) в центре круга равно среднему арифметическому ее значений на окружности.

14. Ряды Тейлора и Лорана.

З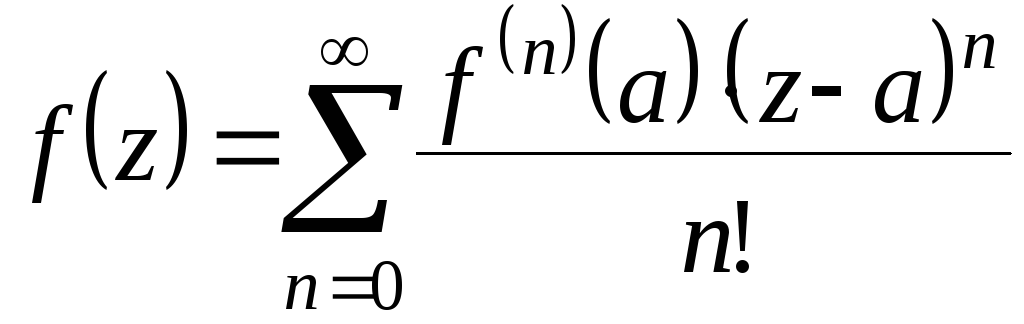аданаf(z) – аналитическая функция в областиG, задан замкнутый контурв. И пусть точка, а точкаzявляется некоторой точкой области. Возьмем произвольную точку а, которая находится в плоскости, тогда формула ряда Тейлора для функцииf(z) определяется равенством:

(1)

Теорема: функция f(z) представлена своим рядом Тейлора в любом круге с центром в точке а, на котором она аналитична. Во всякой замкнутой области ряд Тейлора сходится равномерно.

Разложение функции f(z) в ряд Тейлора (1) справедливо для аналитический функций радиусаr. Но иногда приходится рассматривать и другие функции. Например, когдаf(z) является аналитической всюду, кроме точкиz=a, а областью аналитичности может служить кольцо. Пусть теперь функцияf(z) аналитична в этом кольце.

Представим функцию в виде ряда (2), где коэффициентывычисляются по формуле (3):

(2)

(3)

В формуле (3) - эта любая окружность с центром в точке а и радиусом, удовлетворяют.

Справедлива следующая теорема:

Пусть f(z) аналитична в кольце, когда он разлагается в ряд Лорана, при этом разложение единственное. Коэффициенты вычисляются по формуле, где - окружность, для которой справедливо это равенство, а радиус окружности удовлетворяет. Полученный ряд сходится равномерно.

15. Особые точки. Классификации особых точек.

Точка называется особой точкойf(z), если в областифункцияf(z) является аналитической, а в точкеаналитичность нарушается. В основу классификации изолированных особых точек лежит либо вид разложения функцииf(z) в ряд Лорана, либо поведение функцииf(z) в окрестности этой особой точки. Дадим классификацию особых точек в зависимости от поведения функции в ее окрестности.

1. Изолированная особая точка 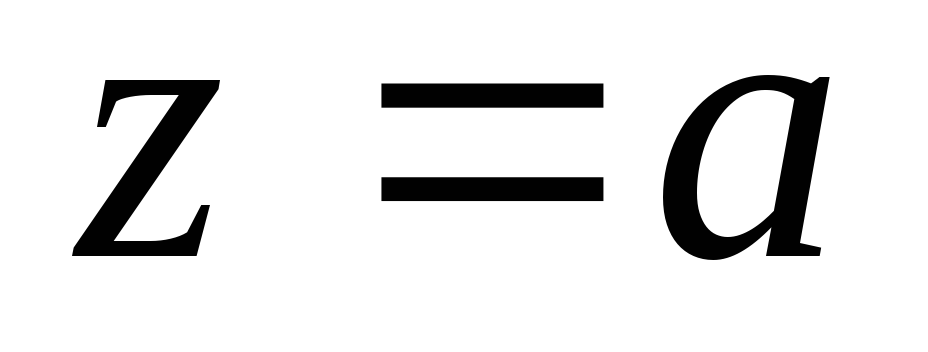называется устранимой особой точкой, если существует конечный предел:

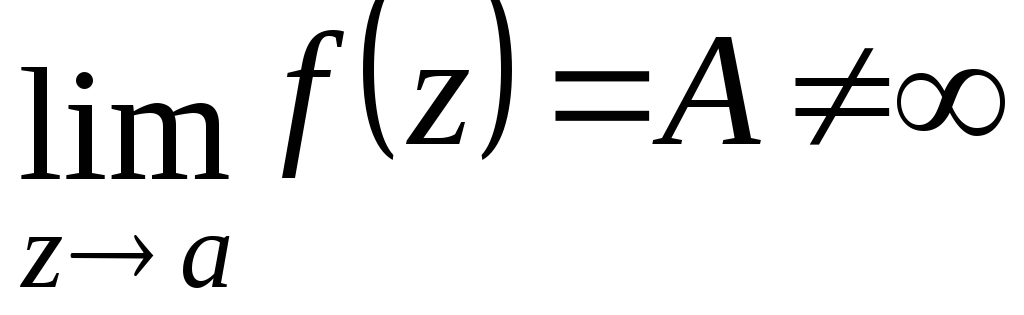
2. Назовем изолированную особую точку полюсом, если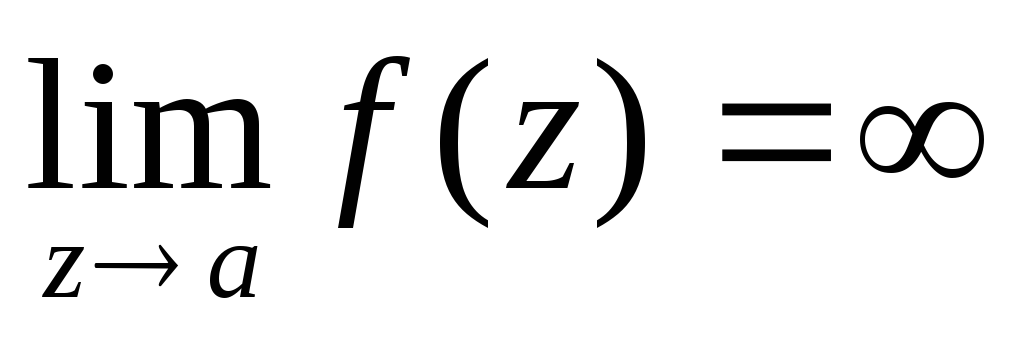, то есть модуль функцииf(z) при.

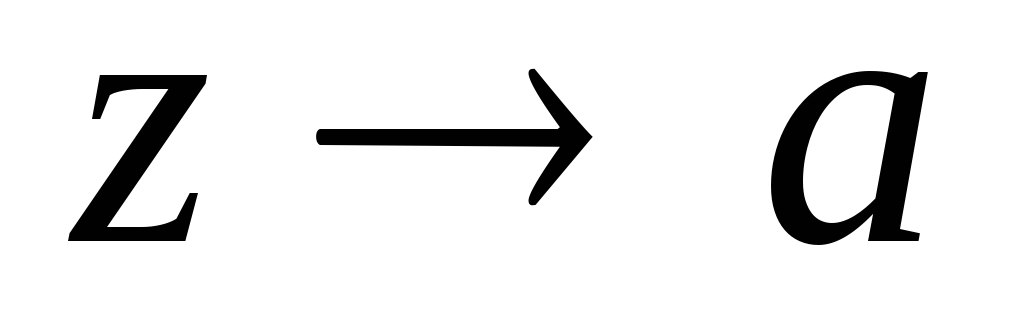3. Изолированная особая точка называетсясущественноособой точкой, если не существует.

Из определения особой точки типа полюс в точке следует, что если функция f(z) имеет полюс в точке, то функцияв точкеравна нулю. И эта функция аналитична в точке, а это означает что.

Справедливо и обратное, если точка является нулем функцииg(z), то функцияимеет в этой точке полюс. Будем называть порядком полюсапорядок нуля в точкефункции. Для того, чтобы точкабыла полюсом порядкаk, разложение функцииf(z) в точкеимела вид:

Или ту же самую функцию f(z) в точкеможно представить следующим образом:

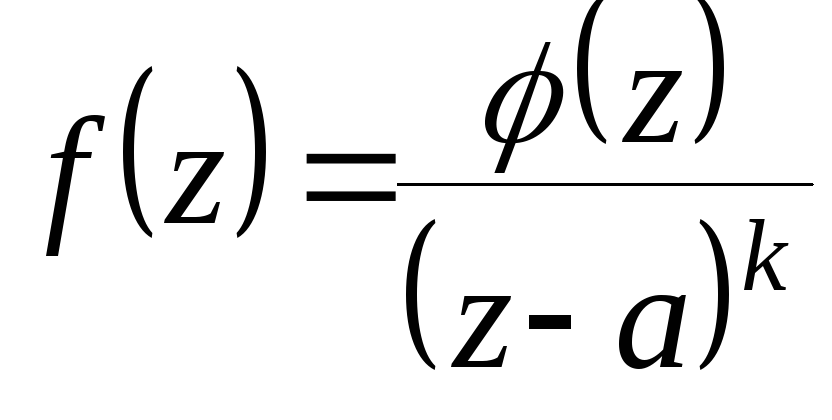
Где функция аналитична в точкеи не равна нулю в этой точке.