16. Понятие о вычете. Общая формула определения вычета относительно полюса.

Вычетом функции f(z) в точкеz=aприназывается число, которая вычисляется по формуле. Где- достаточно малая окружность радиуса, и такая, что в ней нет других особых точек. В этом случае величина вычета не зависит от величины радиусы. Вычетf(z) в точкеz=aобозначается.

Из формулы

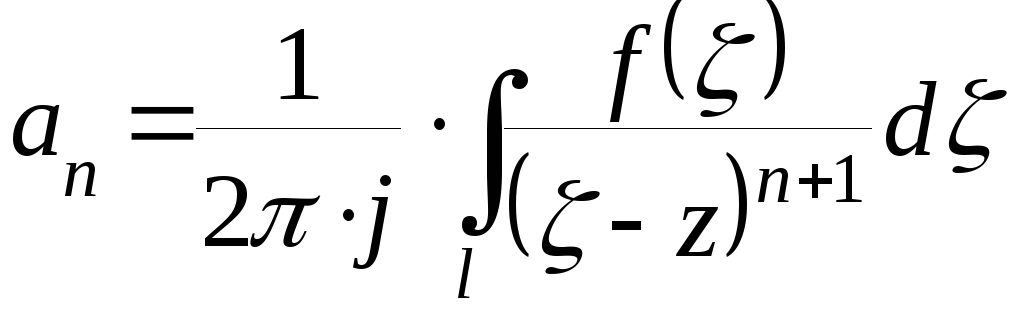
Следует, что вычет в точка z=aопределяется по формуле:

(1)

То есть вычет функции f(z) в точкеz=aравен коэффициенту. Это коэффициент при разложении ряда Лорана. Если особая точка устранена, тоf(z) вычет равен нулю. Это определение вычета справедливо для конечных особых точек, когда.

С помощью вычетов можно существенно упростить вычисление интегралов от функции комплексного переменного. Вычисление интегралов можно свести к вычислению вычетов подынтегральной функции в особых точек. Пусть - спрямляемый контур иG– область, ограниченная этим контуром. Пусть функцияf(z) аналитична в областиGза исключением конечного числа точек. Тогда областьGи контурвнутри этой области – изолированные точки. Вокруг каждой из этих точек выделяем окружности.

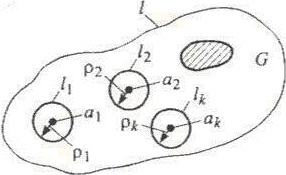
Т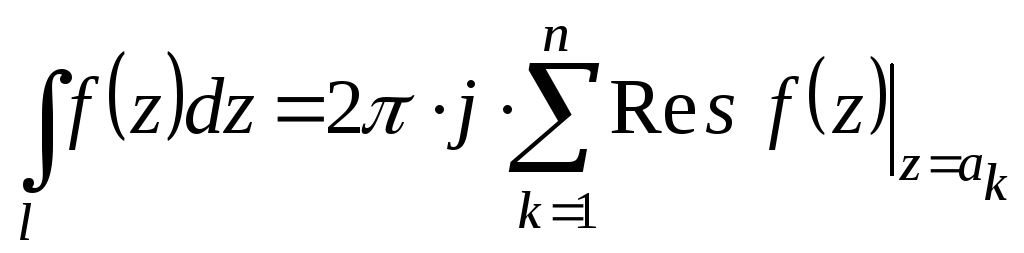огда справедлива формула:

(2)

Пусть функция f(z) имеет в точкеz=aполюс порядкаk, тогда ее разложение в ряд Лорана имеет вид:

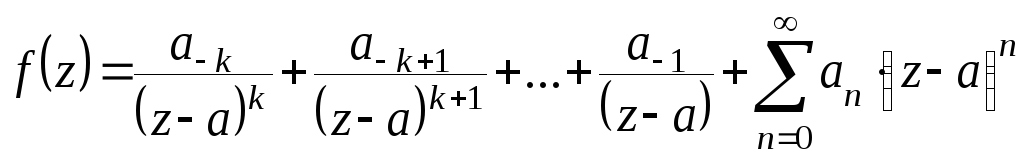
Полюс же в этой точке будет вычисляться по этой формуле:

(3)

Если порядок полюса равен 1, то вычет вычисляется по формуле

(4)

Если при этом f(z) представляет собой отношениеP(z) иQ(z), которые аналитичны в точкеz=a, то есть

Тогда

(5)

17. Интеграл Лапласа. Аналитичность изображения.

1. Функция 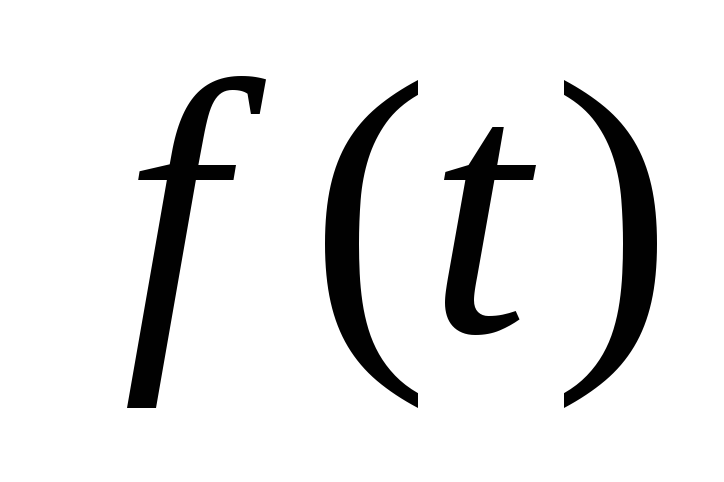непрерывная для всех значений. Непрерывность может быть нарушена лишь в отдельных точках, которые являются точками разрыва непрерывности первого рода, причем число всех точек должно быть конечным на любом интервале ограниченной длины.

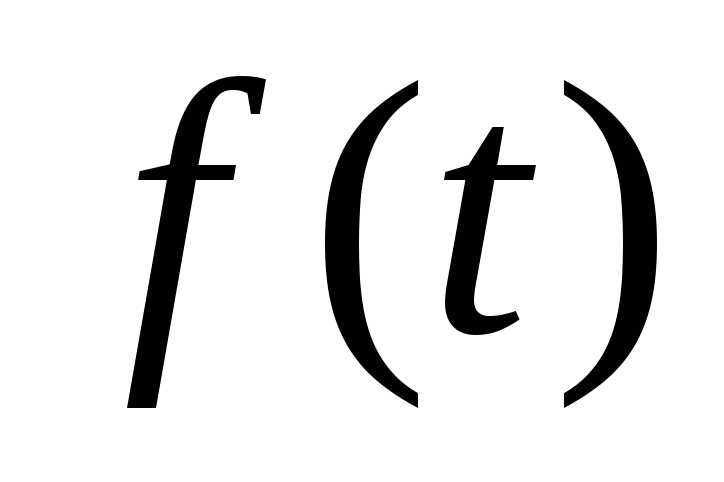2. Функция равна нулю для всех значений переменногоt, которое удовлетворяет неравенству.

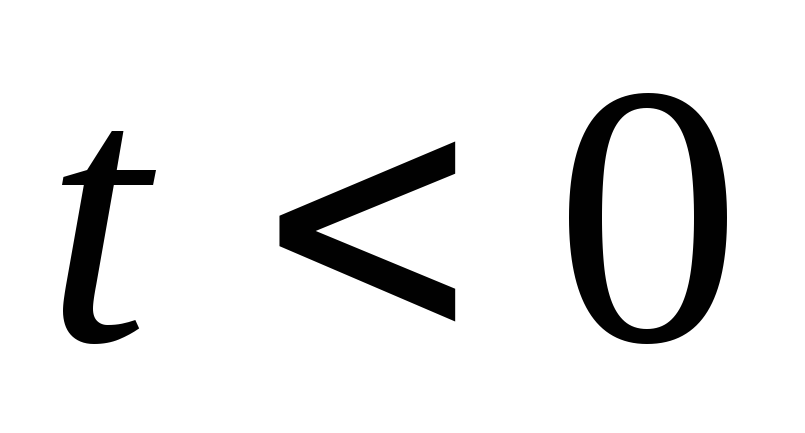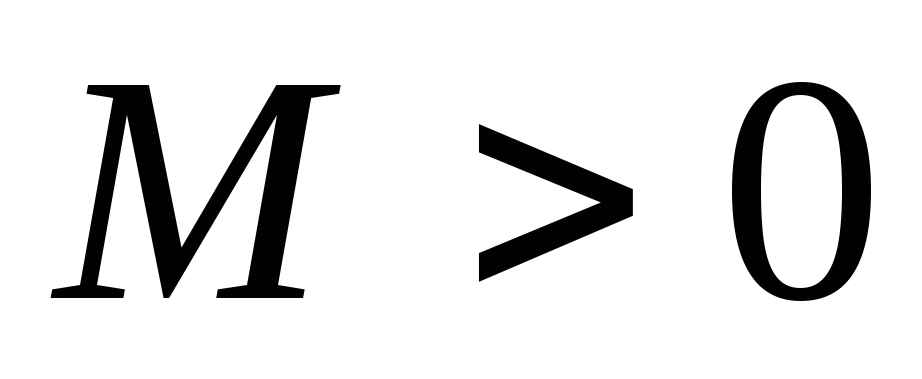3. Функция имеет ограниченный порядок возрастания, то есть можно указать такие постоянные числаи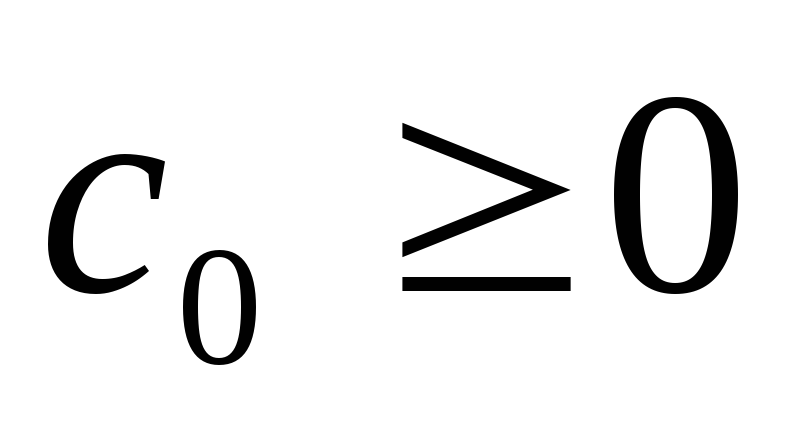, при которых выполняется неравенство

, для всех.

(1)

(2)

(3)

Функция , определяемая равенством (1) называется изображением по Лапласу оригиналаf(t). Этот несобственный интеграл определяется как предел. Все функции и процессы в системах удовлетворяют равенству (3). С помощью уравнения (1) устанавливается соответствие междуf(t) и ее изображениемF(s). Символ преобразования будем записывать в виде (3). Интеграл Лапласа будет сходящимся, если существует предел правой части равенства (2). Установим, какие функции можно преобразовать по Лапласу. Ответ дает следующая теорема:

Если f(t) является оригиналом, то эта функция преобразуема по Лапласу, а ее изображение F(s) определено в полуплоскости , где- показатель роста функцииf(t).

Доказательство.

Предположим, что интеграл правой части (1) выполняется в полуплоскости .Если теперь учесть условие (3) существования оригинала, то можно получить следующую оценку:

Но справедливо такое равенство:

и поэтому справедливо соотношение:

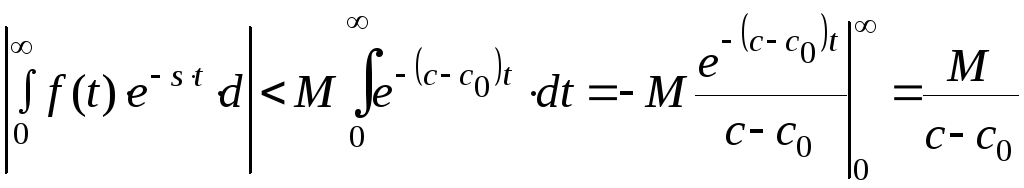
(4)

Так как , то приинтеграл Лапласа сходится. И, следовательно,f(t), которая является оригиналом преобразования по Лапласу, то ее изображениеF(s) определяется в той же части полуплоскости.

Из доказательства следует, что существует интеграл , то есть при соблюдении условия, что действительная часть больше, интеграл Лапласа не только сходится, но и расходится абсолютно.