18. Формула обращения.

Формула обращения:

Формула обращения устанавливает связь между изображением и оригиналом.

Теория.

Оригинал f(t) в точках непрерывности определяется равенством:

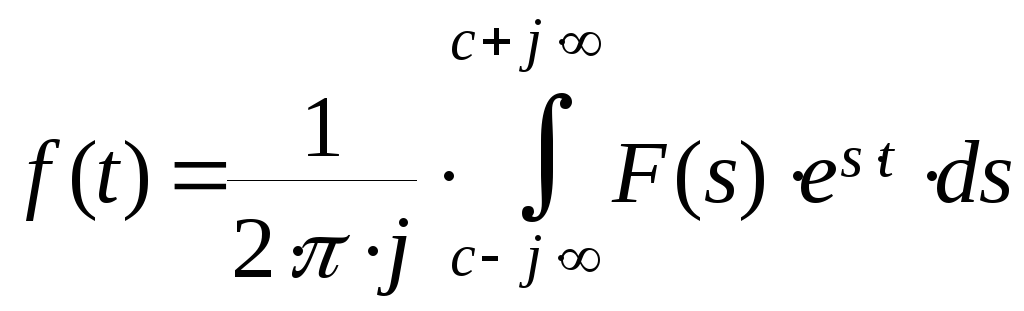(1)

F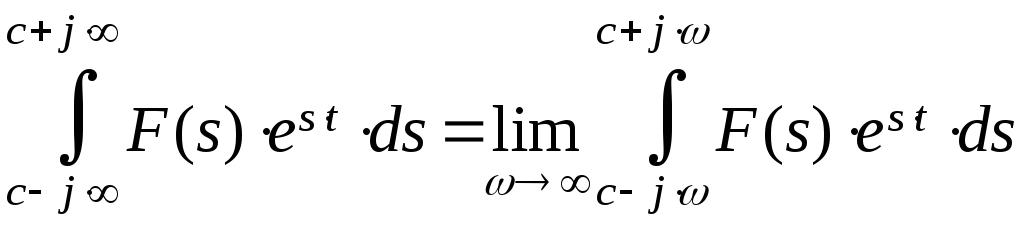(s) – изображение по Лапласу оригиналаf(t), а интеграл в правой части этого равенства понимается в смысле главного значения, то есть:

И берется вдоль прямой, параллельной оси и расположенной в полуплоскости .

Доказательство

Т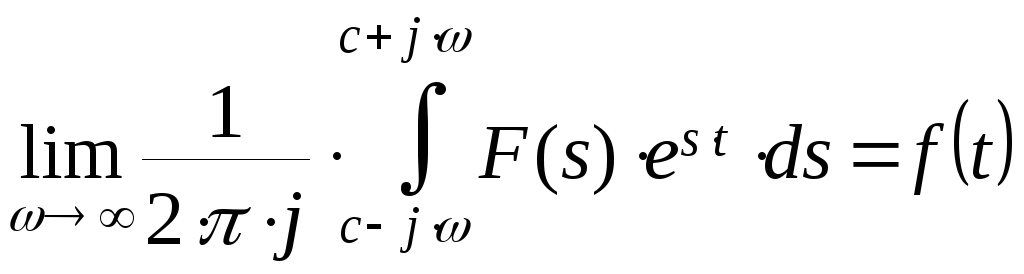еорема будет доказана, если удастся установить:

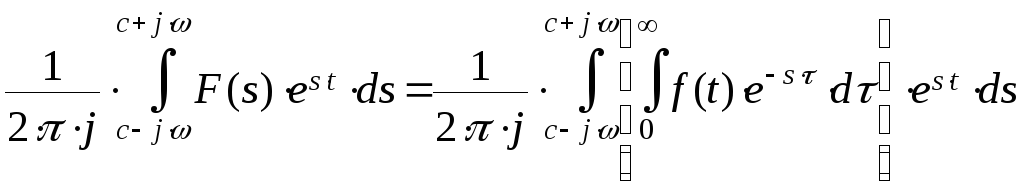
При сходится равномерно. Поэтому можно заменить порядок интегрирования:

Теперь вычисляем:

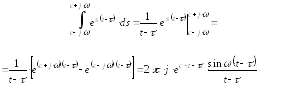
Введем новую переменную и обозначим ее значение:

Тогда

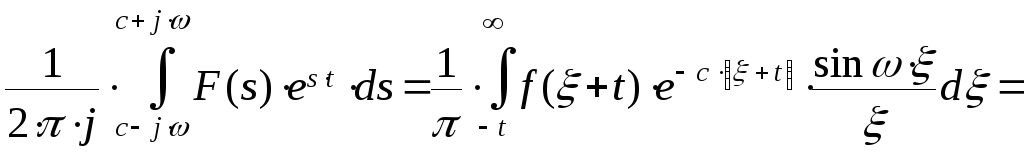
А теперь рассмотрим каждый из интегралов:

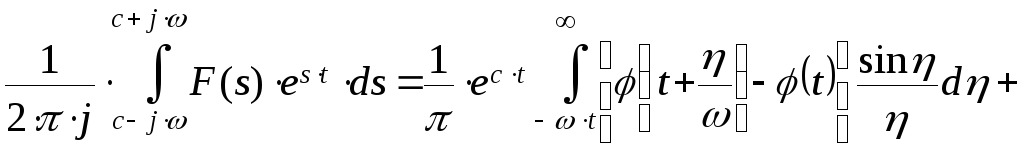
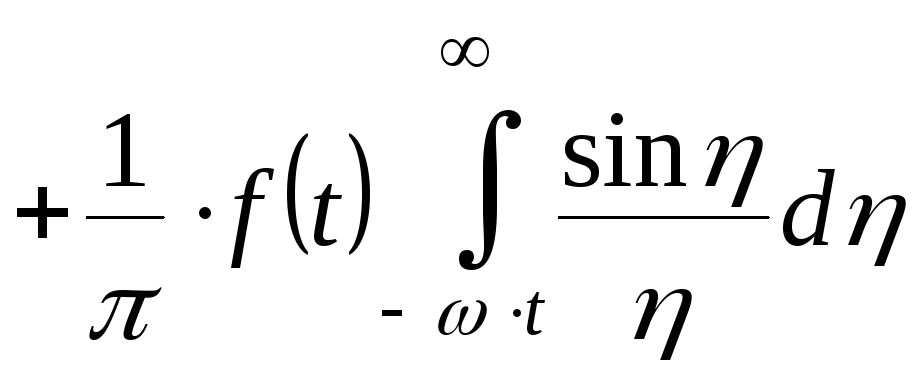
(2)

Устремим и обозначим.

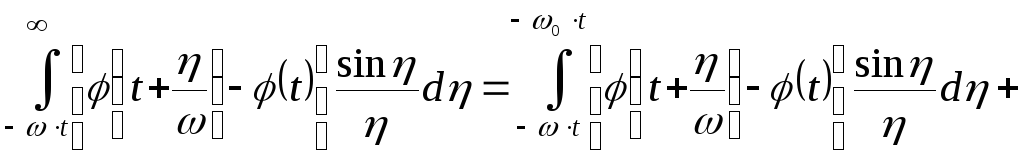(3)

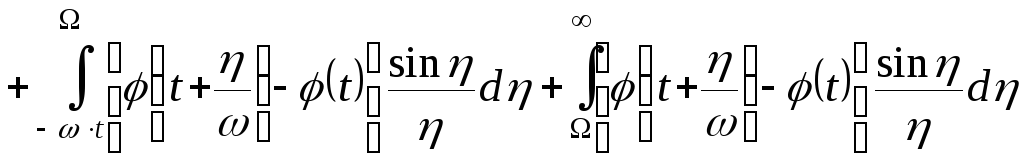
Функция f(t) – оригинал,ограничена. Все интегралы правой части последнего равенства являются сходящимися. Значит, что интервалбудет меньше малого положительного числа. Значенияtхарактеризуют собой точки функцииf(t), то есть при фиксированном значениивыполняется, поэтому модуль интерваластремится к нулю.

Окончательно получаем:

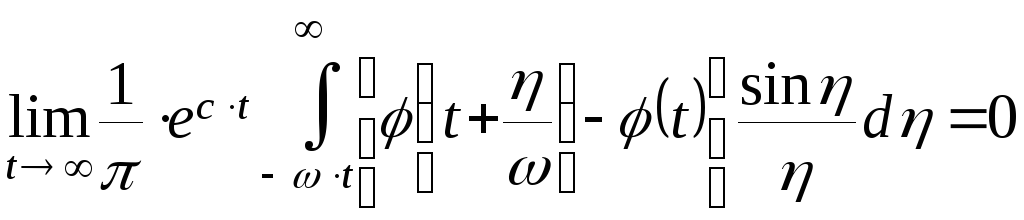
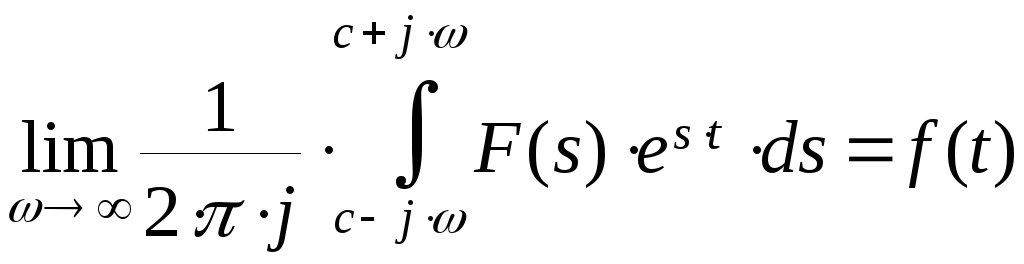
Теорема доказана.

Формула (1) называется формулой обращения. С ее помощью устанавливается связь между F(s) и соответствующего ему оригиналаf(t). Процесс получения оригинала по заданному изображению представляет собой обратное преобразование Лапласа:

, при(4)

Это обстоятельство показывает, что f(t) = оригинал.

С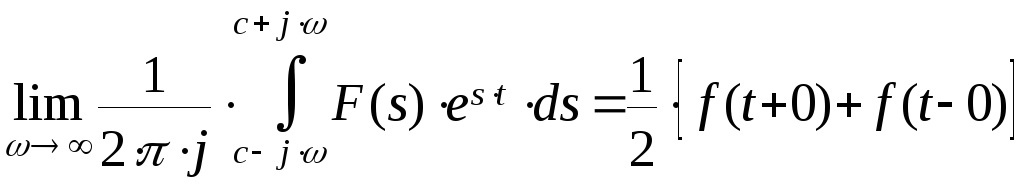ледует отметить, что формула (1) определяет оригинал только в точках его непрерывности. Как и доказательство (3) в точках разрыва функцииf(t) справедливо равенство функции:

(5)

Оригиналам всегда соответствует единственное изображение, которое определяется по формуле (1).

19. Свойства преобразования Лапласа.

1. Свойство линейности.

Если являются оригиналами и их изображения . И если- величины, которые не зависят отtиs, то справедливы следующие равенства:

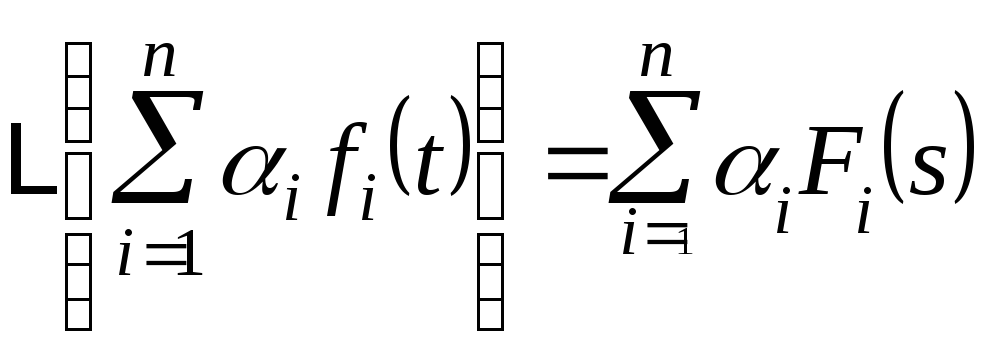(1)

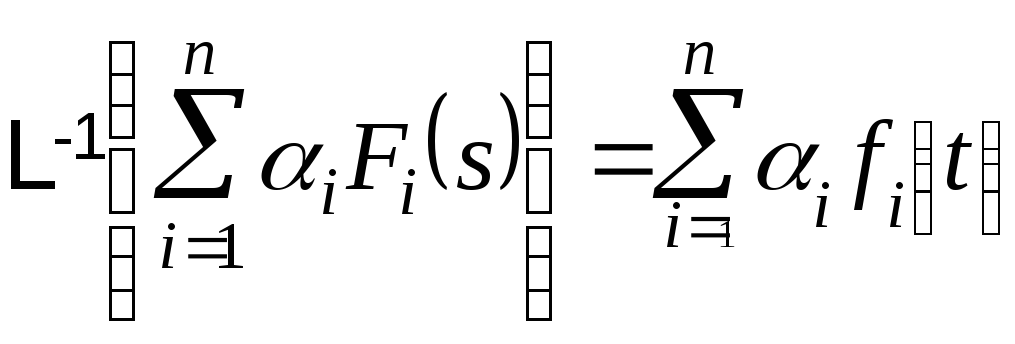(2)

Доказательство

По формуле преобразования Лапласа

Теперь находим

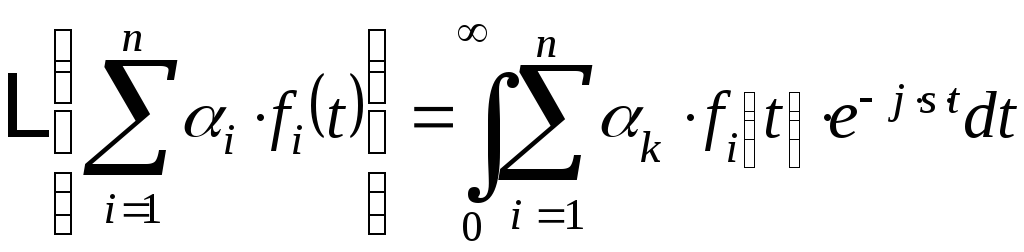
Так как интеграл суммы равен сумме интегралов, а множитель не зависит от переменной интегрированияt, то можно записать:

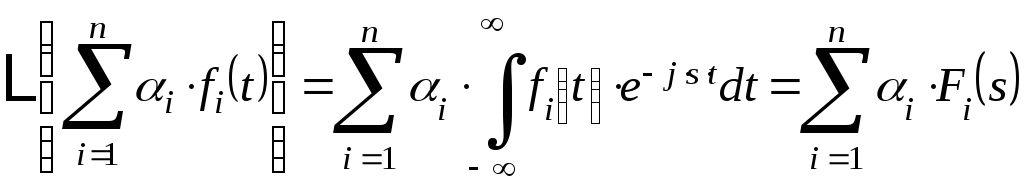
Аналогично показываем справедливость формулы (2):

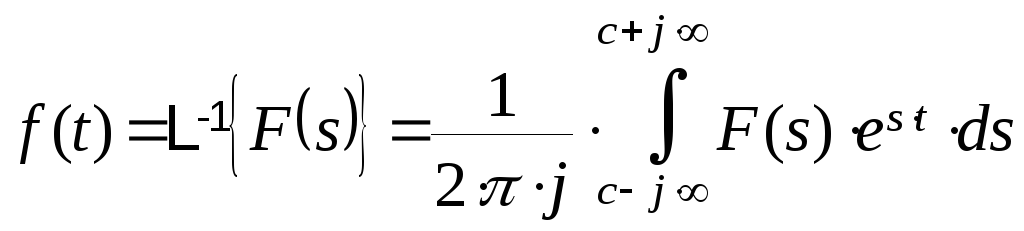
Т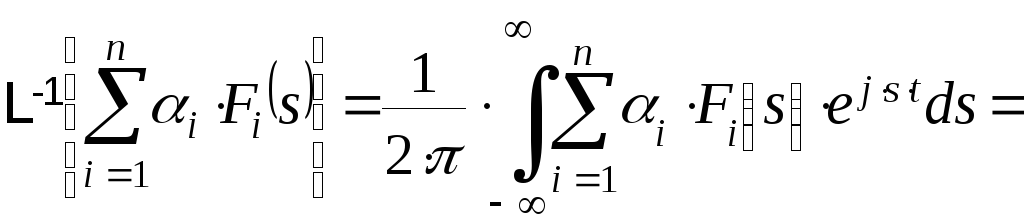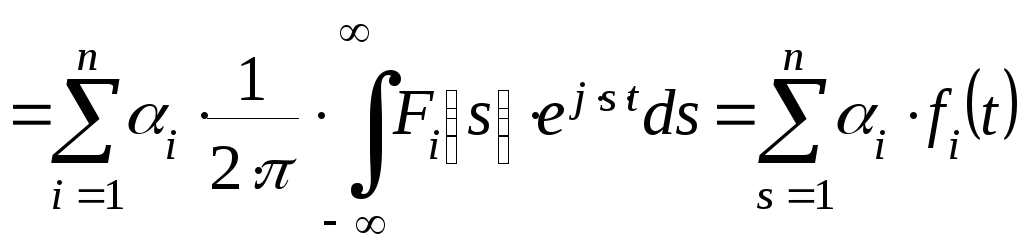еперь берем обратное преобразование Лапласа и по аналогии:

Теорема доказана.

2) Дифференцирование в области оригиналов.

Е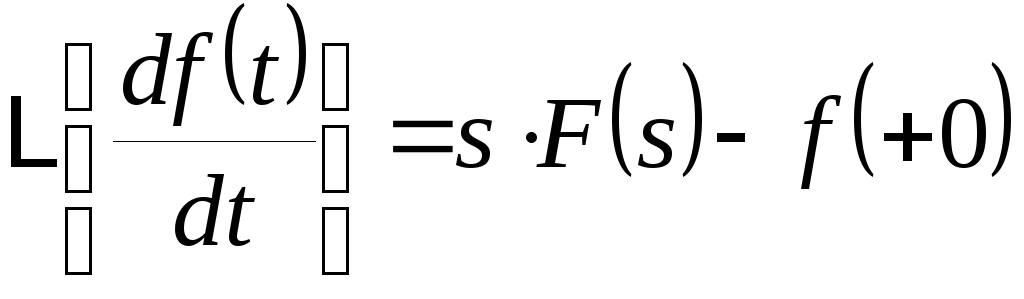слиf(t) является оригиналом и ее производная также является оригиналом, и ее изображение по ЛапласуF(s), то справедливо равенство:

(3)

Плюс означает, что значение функции – это значение ее предела при справа, то есть(правосторонний предел).

Доказательство

Воспользуемся равенствами:

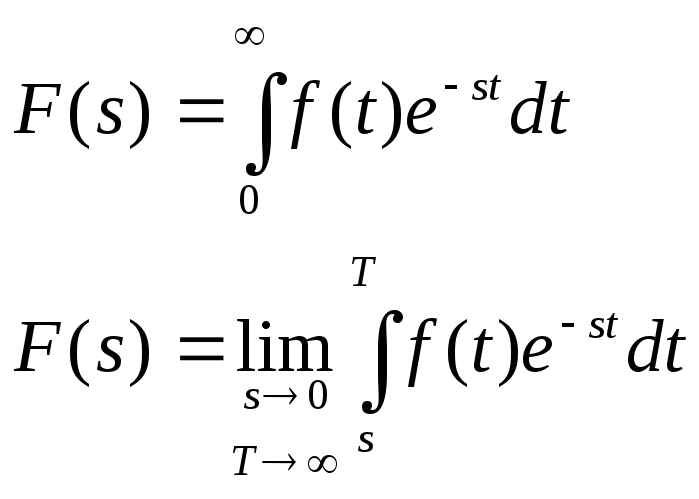
Найдем изображение по Лапласу:

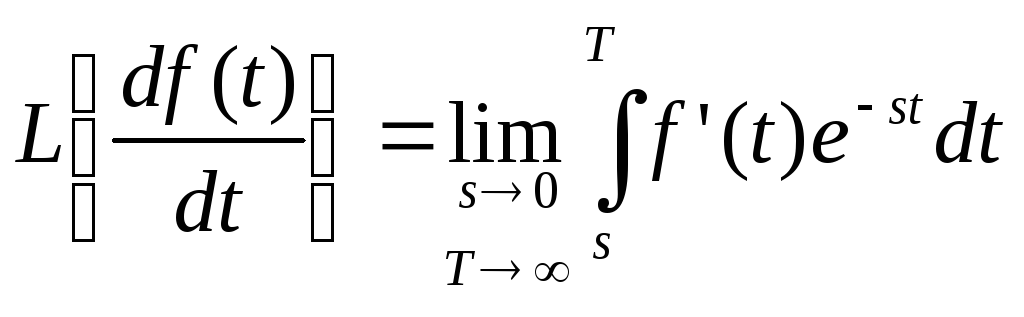
Так как f(t) – оригинал, то для всехсправедливоили, тогда это справедливо для всех случаем, когда.

Справедливо следующее соотношение

Учтем равенства:

И получим формулу (3).

Если начальное значение функции , то формула (3) принимает вид:

Для второй производной:

Для третьей производной:

И для n– ой производной:

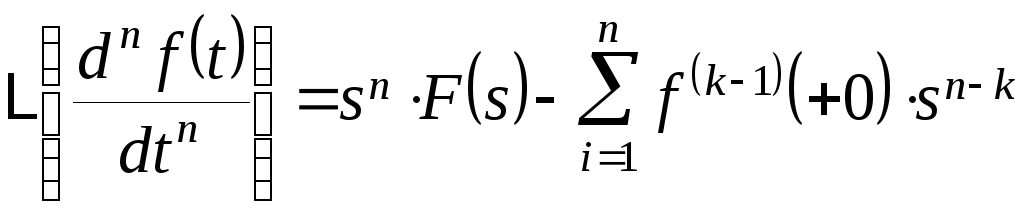(4)

3) Интегрирование оригинала.

Если f(t) является оригиналом, ее изображение F(s), тотакже является оригиналом, а ее изображение по Лапласу:

(5)

Где - постоянная интегрирования.

Доказательство

П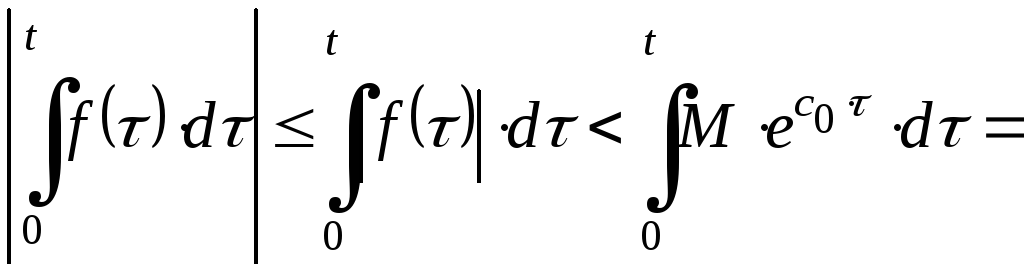режде всего покажем, что интегралявляется оригиналом. Условия (1) и (2) существования оригинала очевидны, так как они выполняются для функцииf(t). А теперь проверил выполнение условия (3). Оценим абсолютную величину заданного интеграла:

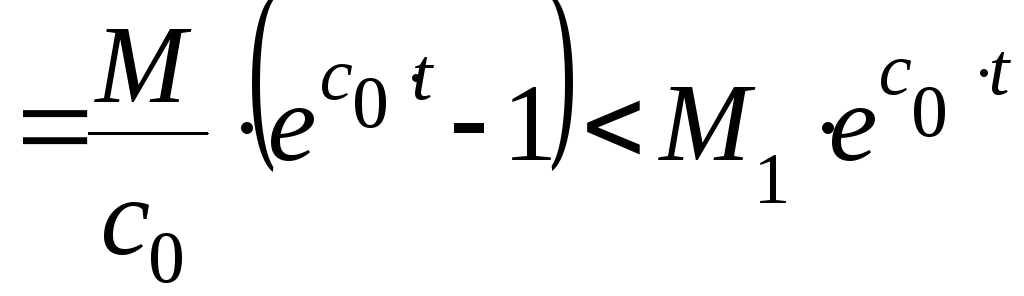
Следовательно, условие (3) также выполняется. Убедимся теперь в справедливости (5):

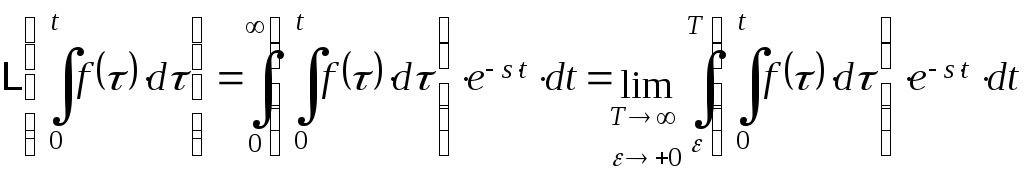
И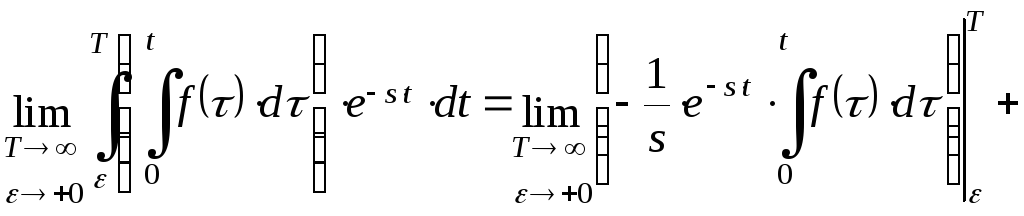нтегрируя последнее равенство по частям, получим:

М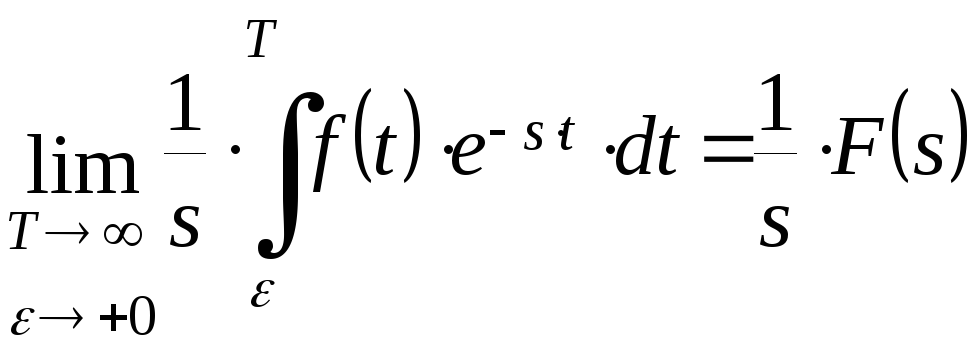одуль выражения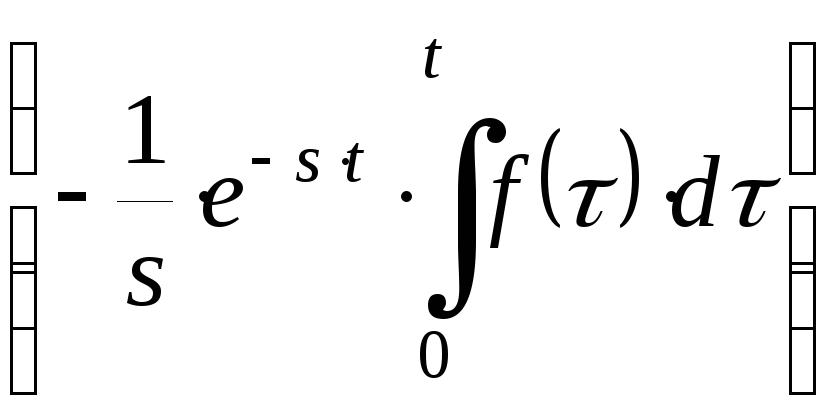для всехменьше или равен, где, то предел первого слагаемого равен нулю.

(6)

И на основании свойств линейности получим формулу (5).

Теорема доказана.

4) Смещение в области оригинала.

Если f(t) – оригинал иF(s) – его изображение, то изображение смещенного оригинала, гдеa– положительное число, определяемое равенством:

(7)

Доказательство

При доказательстве используется:

Введем новую переменную . Тогда будем иметь:

Умножим это равенство слева и справа на . Будем считать, чтоaне зависит отt. Тогда получим:

Вносим под знак интеграла и получаем:

Теорема доказана.

5) Смещение в области изображений.

Если f(t) – оригинал иF(s) – его изображение, а – любое число, включая и комплексное, то справедливо:

(8)

Доказательство

Воспользуемся формулой прямого преобразования Лапласа:

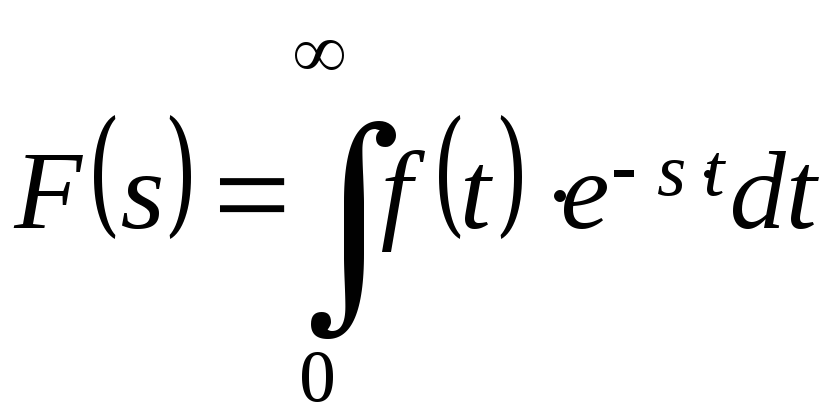
И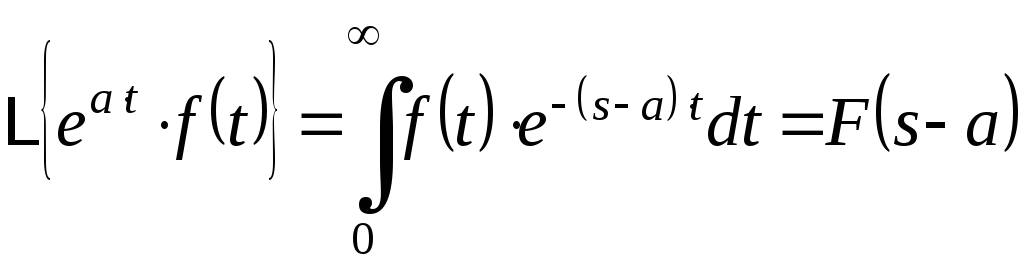найдем:

Теорема доказана.