Вариационные задачи на условный экстремум. Связи вида

Вариационными задачами на условный экстремум называют задачи, где требуется найти экстремум функционала , при чем на функции, от которых зависит этот функционал, накладываются некоторые связи.

Например, надо найти экстремум функционала:

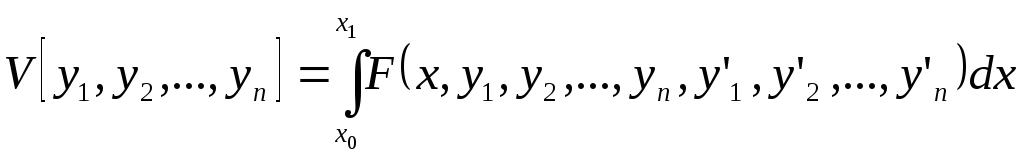
при наличии условий:

Вспомним, как решается аналогичная задача. При исследовании на экстремум функции при наличии связей. Наиболее естественный путь заключается в том, чтобы решить систему уравнений. Уравнения будем считать независимыми от каких-нибудь переменных, например,. Эта система имеет вид:

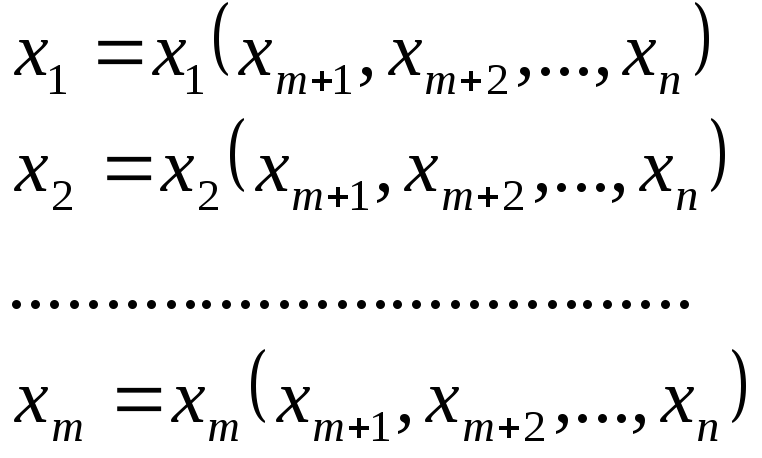
Найденные значения подставим в подынтегральную функцию. При этом функциястановится функцией отпеременных -. Этим же путем можно решать систему уравнений поставленной ранее задачи, то есть решить систему:

относительно переменных или каких-либо других функций, и, подставляя их выражения в функционал.

В результате чего мы получаем функционал от этого функционала, который зависит отуже независимых функций, применяя уже известные методы.

Однако как для функций, так и для функционалов обычно более удобен другой метод решения, называемый методом неопределенных множителей, сохраняющий полное равноправие всех переменных. Этот метод при исследовании на экстремум функции при наличии связейзаключается в том, что составляется некоторая новая функция:

где - некоторые постоянные множители, а функцияуже исследуется на безусловный экстремум, то есть находится производная. Она приравнивается к нулю, и получается система уравнений. Затем добавляется уравнение связи, из которых находимнеизвестныхи. Также используется тот же подход. Можно решить задачу на условный экстремум функционал:

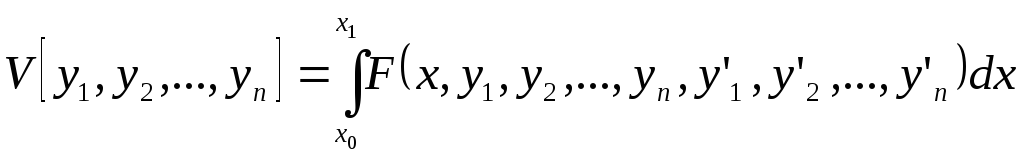
при наличии уравнения связей:

Составляется вспомогательный функционал:

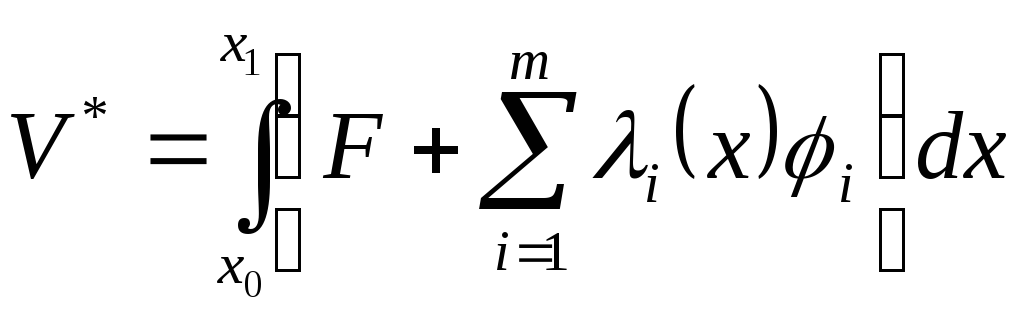
Или:

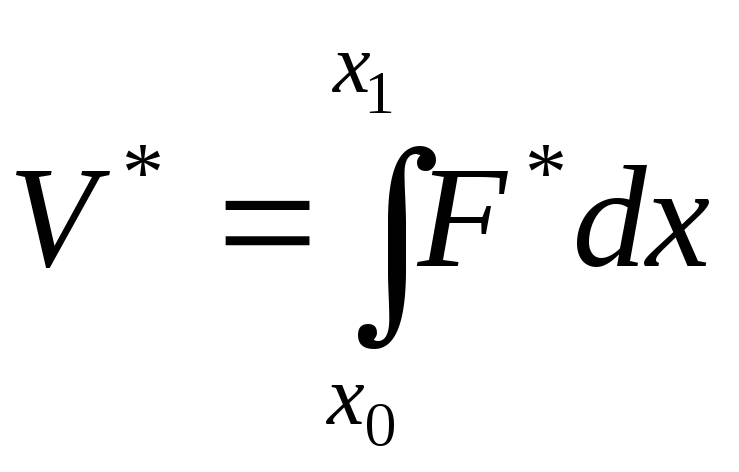
где введено условие:

Этот функционал исследуется на безусловный экстремум.

Здесь составляется уравнение Эйлера:

25