Простейшая задача с подвижными границами

При исследовании функционала предполагалось, что граничные точкизаданы. Предположим, что одна или обе точки могут перемещаться. Тогда класс допустимых кривых расширяется. Кроме кривых сравнения, имеющих общие граничные точки, можно уже брать и кривые со смещенными граничными точками. Поэтому, если на какой-либо кривойдостигается экстремум по отношению к более узкому классу кривых, имеющих общие граничные точки с кривой, и, следовательно, должна быть выполнена основная необходимая для достижения экстремума задача с неподвижными границами.

Функция должна быть решением уравнения Эйлера:

Кривые , на которых реализуется экстремум, должны быть экстремалями.

Общее решение уравнения Эйлера:

содержит две произвольные постоянные, чтобы их определить, надо иметь два условия.

Для задачи с подвижными границами это условие выполнено в виде: - начальные точки фиксированы.

В задачах с подвижными границами одно или оба эти условия отсутствуют, и недостающее условие для определения произвольных постоянных общего решения уравнения Эйлера должны быть получены из основного необходимого условия экстремума:.

Таким образом, если в задачах с подвижными границами решение достигается на решении уравнения Эйлера:

то в дальнейшем можно рассматривать значение функционала лишь на функциях этого семейства. При этом функционал превращается в функцию параметровии пределов интегрированияи, а вариация функционала совпадает с дифференциалом этой функции. Для упрощения будем считать, что одна из граничных точек, например, закреплена, а другаяможет перемещаться и переходит в точку. Или, как принято в вариационном исчислении, в точку.

Допустимые кривые будем считать близкими, если модули вариацийималы, и малы модули приращенийи. Вариациииназываются вариациями в точкахи. Экстремали, проходящие через точку, образуют пучок экстремалей. Функционална кривых этого пучка превращается в функцию аргументови.

Если кривые пучка в окрестности рассматриваемой экстремали не пересекаются, то можно рассматривать как однозначную функциюи, так как заданиеиопределяет экстремаль пучка и тем самым определяет значение функционала (рис. 1).

Вычислим вариацию функционала на экстремалях пучка. При перемещении граничной точки из положенияв положение. Так как функционалVна кривых пучка превращается в функцию двух аргументови, то вариация совпадает с дифференциалом этой функции. Выделим из приращенияглавную линейную по отношению кичасть.

Имеем:

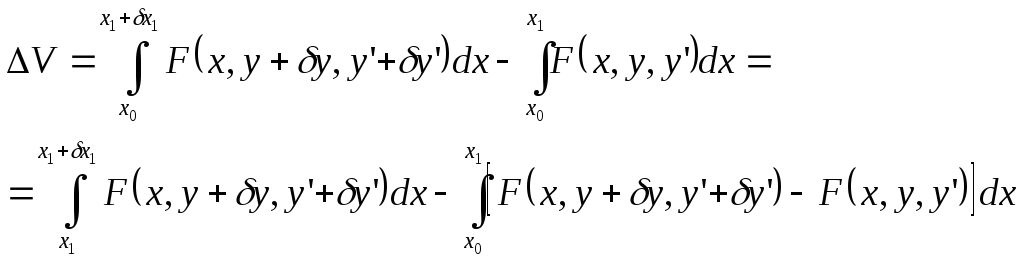(1)

Первое слагаемое правой части преобразуется, используя теорему о среднем:

;

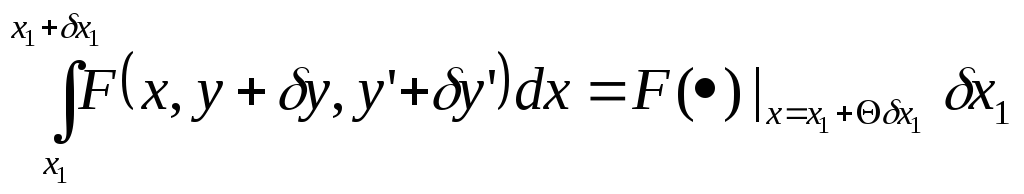В силу непрерывности функции , будем иметь:

Итак:

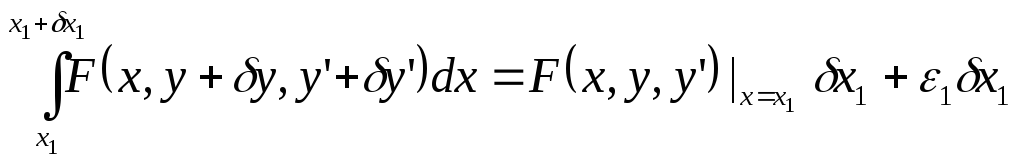
Второе слагаемое правой части (1) преобразуем путем разложения подынтегральной функции по теореме Тейлора:

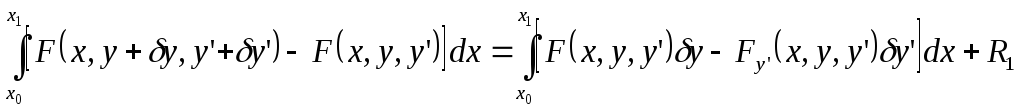
является бесконечно малой величиной большего порядка, чеми. В свою очередь линейная часть функционала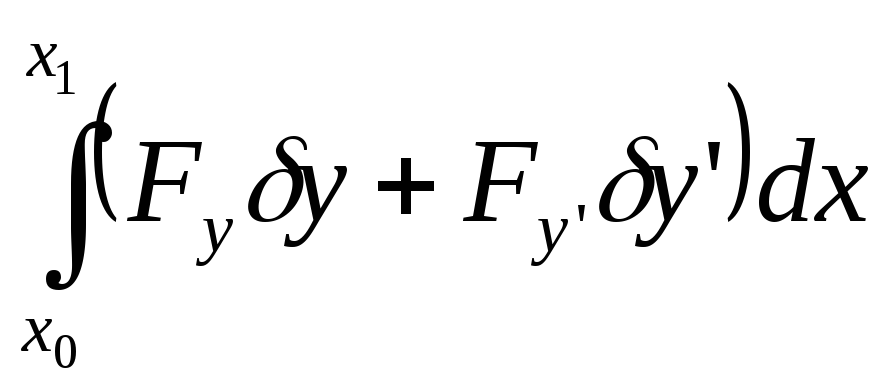может быть преобразована путем интегрирования по частям второго слагаемого подынтегральной функции:

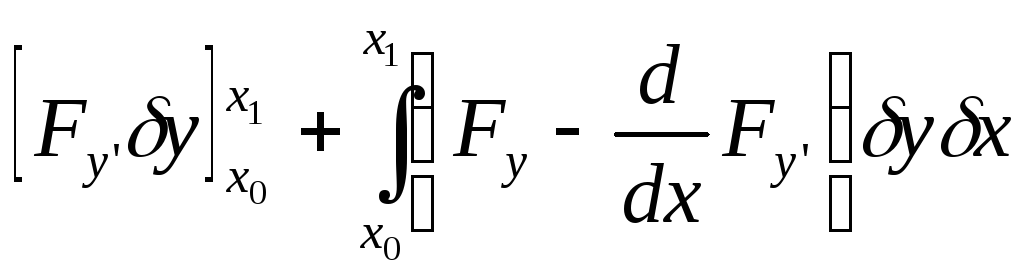
Значения функционала берутся лишь на экстремалях, следовательно, справедливо равенство:

Так как граничная точка закреплена, то это значит, что, следовательно:

Здесь важно знать, что не равно, так как- это приращениепри перемещении граничной точки в точку с координатами. А- это приращение ординаты к точке. При переходе от экстремали, проходящей через две граничные точки, к экстремали, проходящей через точкии(Рис. 2).

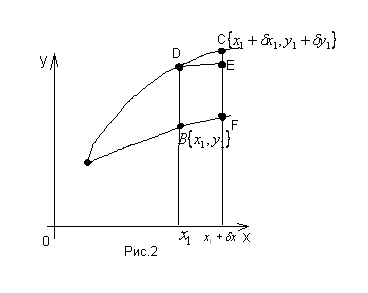
Из рисунка видно, что справедливы равенства:

,,,,

При этом приближенное равенство справедливо с точностью до бесконечно малых более высокого порядка.

Итак, окончательно получаем:

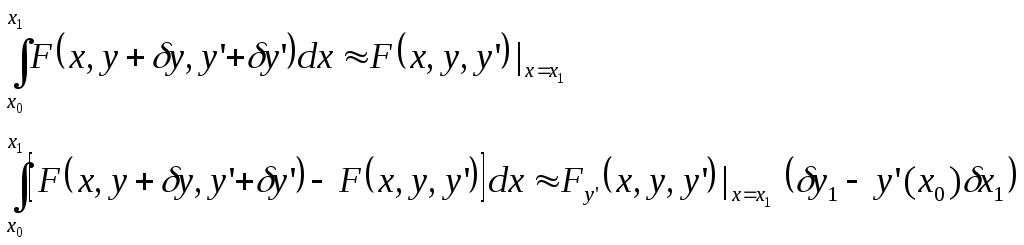
Где приближенные равенства справедливы с точностью до бесконечно малых более высокого порядка относительно и.

Следовательно, из уравнения (1) получаем:

Или:

Где функция, в которую превратился функционал на экстремалях.

А и- приращение координат граничной точки.

Основное необходимое условие экстремума принимает вид:

(2)

Если вариации инезависимы, то отсюда следует справедливость равенств:

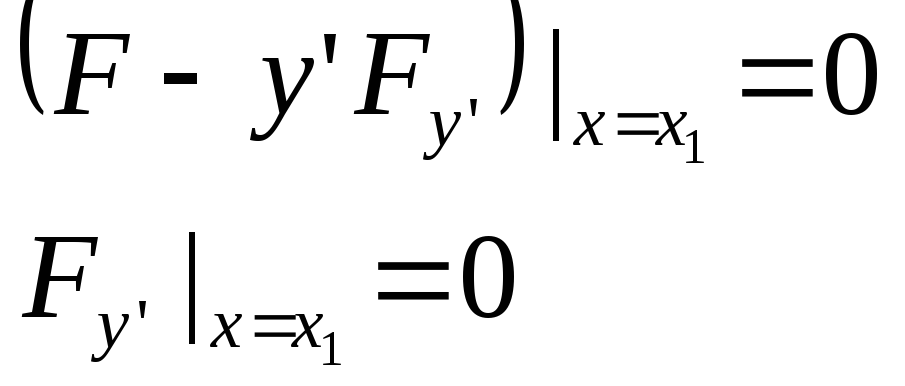
Однако часто приходится рассматривать случай, когда эти вариации зависимы. Пусть граничная точка может перемещаться по кривой, тогда условие (2) принимает вид:

Или, так как меняется произвольно:

Это условие устанавливает зависимость между ив граничной точке и оно называется условием трансверсальности. Условие трансверсальности совместимо с условиемпозволяет определить одну или несколько экстремалей, на которых может достигаться экстремум.

Если граничная точкаможет пересекаться по некоторой кривой, то совершенно также обнаружим, что в точкедолжно выполняться условие трансверсальности: