Функционалы вида

Задан функционал более общего случая:

и граничные условия:

Будем варьировать функцию , последовательно изменяя индексы. При этом остальные функции оставляем неизвестными. В этом случае исходный функционалпревращается в функционал, зависящий от одной функции. То есть имеем соотношение:

Отсюда следует, что для функционала, который мы получили, уравнение Эйлера принимает вид:

Так как это рассуждение применимо к любой функции , то мы получим систему уравнений Эйлера. Эти уравнения Эйлера определяют 2nпараметрических семейства интегральных кривых. Это семейство экстремалей в данной вариационной задаче.

Если в частности, функционал:

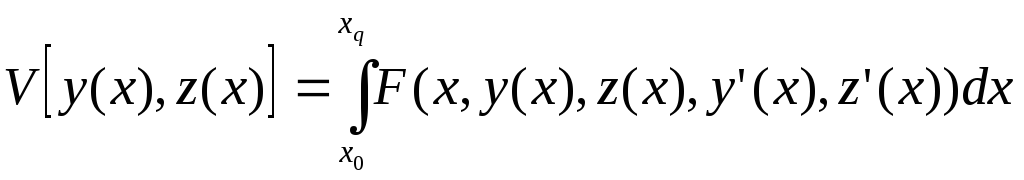
зависит от двух функций. Заданы граничные условия:

То есть определяем выбор пространственных кривых и.

Варьируя и, мы изменяем нашу кривую так, что ее проекция на плоскостьXYZне изменяется, то есть кривая все время остается на проецируемом цилиндре. Аналогично, фиксируяи варьируя, мы варьируем кривую так, что она остается на проецируемом цилиндре, при этом система уравнений Эйлера запишется следующим образом:

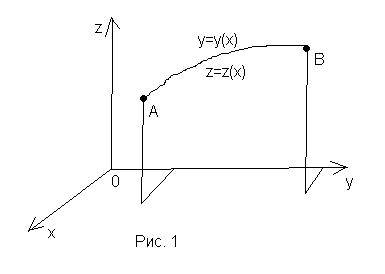
Все сказанное иллюстрирует рисунок 2:

Рассмотрим вторую вариацию функционала .

В результате получаем:

(1)

Введем обозначения:

Тогда:

С учетом обозначений, вторая матрица принимает вид:

И третья матрица:

Введем еще раз обозначения:

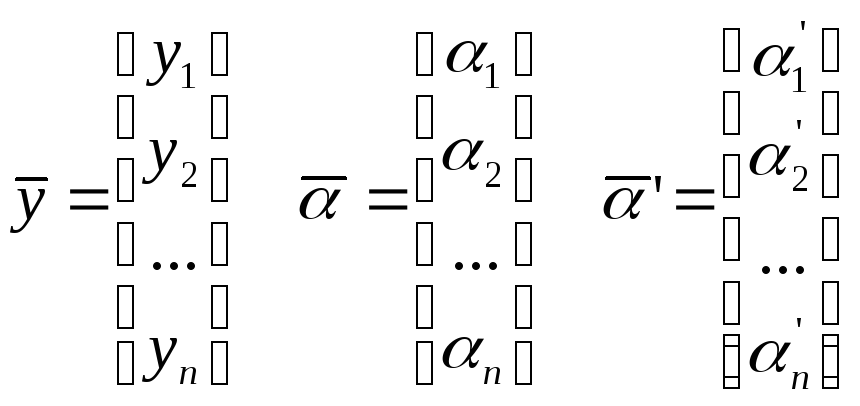
Тогда вторая вариация функционала запишется следующим образом:

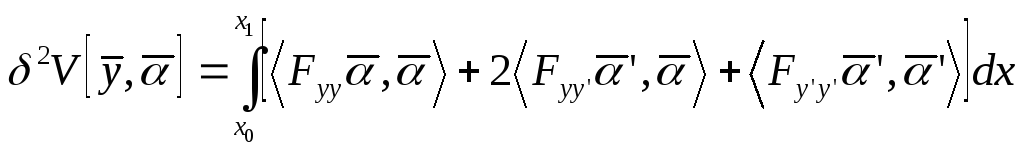(2)

Необходимое условие экстремума функционала имеет вид:

Это условие должно выполняться для всех допустимых установившихся значений .

Вспомним критерий Сильвестра. Это значит, что главные диагональные миноры должны быть не отрицательны. То есть должны выполняться следующие неравенства:

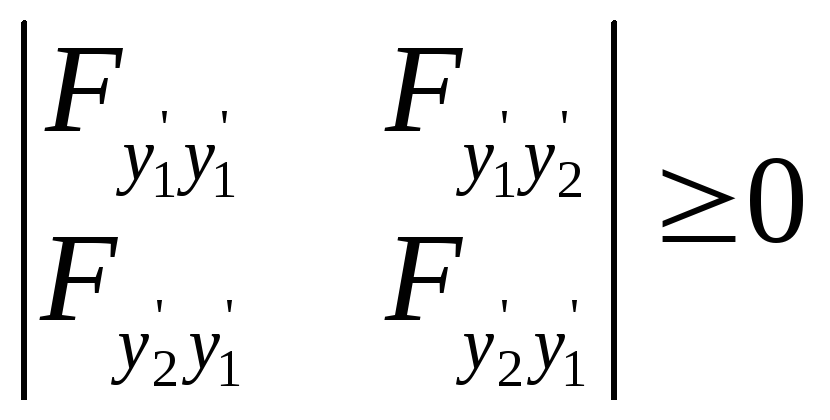
Справедливо следующее утверждение:

Для того, чтобы кривая доставляла слабый минимум функционалу:

достаточно, чтобы выполнялись условия:

1. Кривая 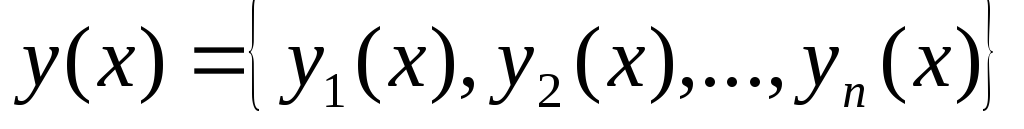должна быть экстремалью, то есть удовлетворяла системе уравнений Эйлера:

2. Все главные диагональные миноры матрицы должны быть строго положительны для любого.

3. Система уравнений Якоби:

(3)

должна иметь решения , которые удовлетворяют начальным условиям:

Аналогично формируется условие слабого минимума для функционала:

Отметим, что при определитель равен нулю:

то точка называется сопряженной по отношению к точке. Поэтому условие (3) можно сформулировать следующим образом:

Отрезок не должен содержать точки, сопряженные с точкой.

Вариационные задачи в параметрической форме

Во многих вариационных задачах решения удобно искать в параметрическом виде. Например, в изопараметрических задачах о нахождении замкнутой кривой заданной длины и ограниченной максимальной площадиSнеудобно искать решение в виде кривой, так как по самому смыслу задачи функция- неоднозначная, поэтому в этом случае решение удобно искать в параметрическом виде:.

Таким образом, в данном случае целесообразно искать экстремум функционала:

с условием:

при этом - постоянная.

Рассмотрим задачу на экстремум функционала:

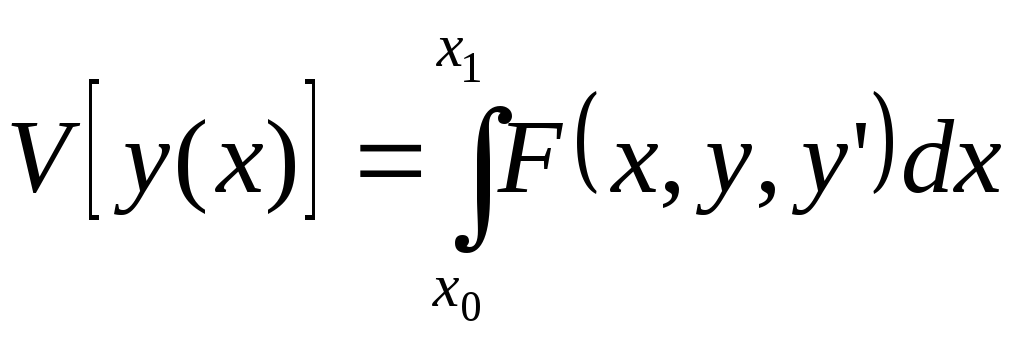
Решение будем искать в параметрической форме . Тогда функционал принимает следующий вид:

Теперь получилось, что подынтегральная функция явно не зависит от времени tи является однородной по отношению к производными(однородность первой степени).

Исходный функционал является непроизвольным функционалом вида:

который зависит от функций и.

Если бы мы перешли к какому-нибудь другому представлению параметрической кривой - , то теперь функционал принял бы вид:

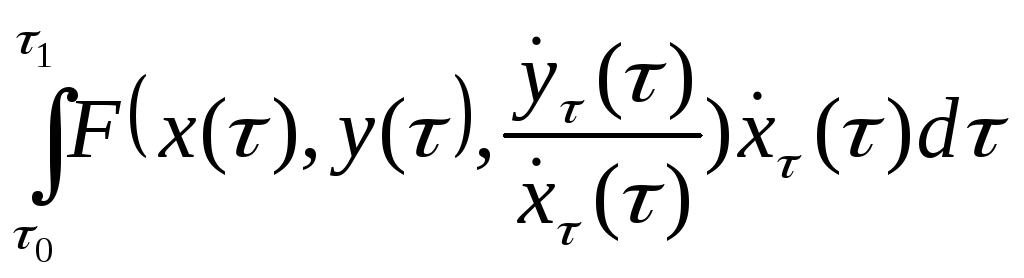
Следовательно, функционал не меняет своего вида при изменении параметрического представления кривой, а зависит от вида кривой.

Справедливо утверждение:

Если подынтегральная функция функционала 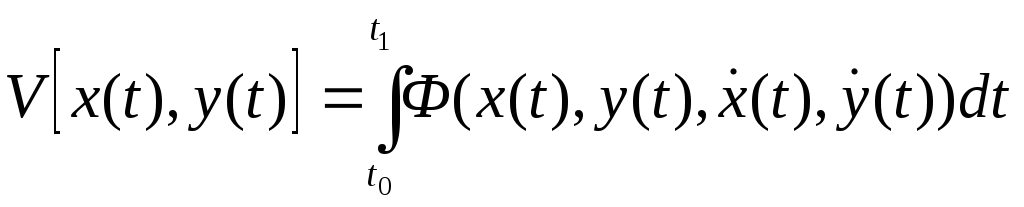не содержитtи является однородной функцией первой степени относительнои, то исходный функционал зависит лишь от вида кривыхи не зависит от формы представления кривой. Теперь рассмотрим функционал общего вида.

Пусть задан функционал:

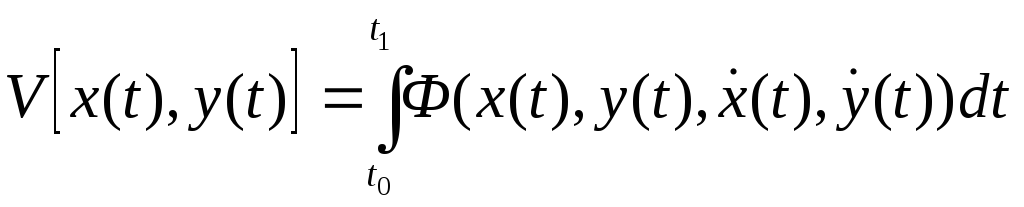
Подынтегральная функция является функцией первой степени:

Перейдем к новому параметрическому представлению: .

Тогда:

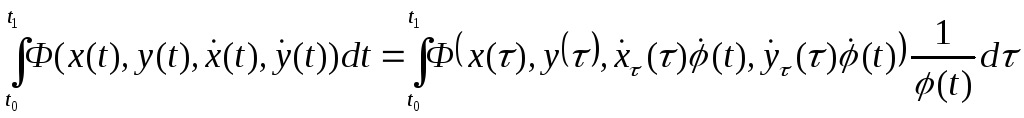
Так как функция является однородной первой степени относительнои, то справедливо:

Откуда:

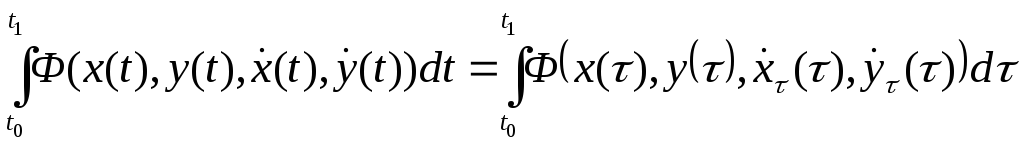
То есть подынтегральная функция не изменилась при изменении параметрического представления для нахождения экстремума функционала , гдеявляется однородной первой степени относительнои.

Для функционала произвольной подынтегральной функции надо решить систему уравнений Эйлера:

В некоторых случаях эти решения не являются независимыми.

Для нахождения экстремума надо взять одно из уравнений Эйлера и проинтегрировать относительно определяющего выбор параметра.