Задача с подвижными границами для функционалов вида

Если при исследовании на экстремум функционала:

одна из граничных точек, например правая точка перемещается, а левая точкаостается неподвижной, или обе точки перемещаются, то экстремум может пересекаться на интегральных кривых уравнения Эйлера:

Если экстремаль достигается на некоторой кривой , то есть достигается максимальное или минимальное значение функционала , по сравнению со значениями этого функционала на всех близких допустимых кривых, среди которых находятся как кривые, имеющие общие граничные условия с кривой, так и кривые, граничные точки, которые не совпадают с граничными точками кривой.

Тогда на кривой достигается экстремум по отношению к узкому классу близких кривых, имеющих общие граничные точки с кривой.

Следовательно, на кривой должны удовлетворяться необходимые условия экстремума с неподвижными граничными точками, и, в частности, криваядолжна быть интегральной кривой системы уравнения Эйлера. Общее решение системы уравнений Эйлера содержит четыре произвольные постоянные. Зная координаты граничной точки, которую мы считаем неподвижной, можно исключить две постоянные. Для определения двух постоянных надо иметь еще два уравнения, которые могут быть получены из уравнения:

При чем при вычислении вариаций будем считать, что функционал задается лишь на решении уравнения Эйлера, так как только на них может достигаться экстремум функционала. При этом функционал превращается в функциюкоординат точки, и вариация функционала превращается в дифференциал этой функции.

Функция будет однозначной, если экстремали пучка с центром в точкене пересекаются, так как точкаоднозначна определяет экстремаль.

Так же, как и в предыдущем случае, последовательно получаем:

Применим теорему о среднем значении в первом интеграле и воспользуемся непрерывностью функции , а во втором интеграле выделим главную линейную часть с помощью формулы Тейлора. После этих преобразований получаем:

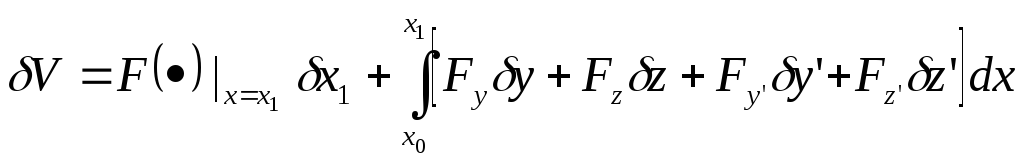
Интегрируя по частям два последних слагаемых, получаем:

Так как значения функционала вычисляется только на экстремалях, то должны выполняться уравнения:

И, следовательно, вариация функционала запишется следующим образом:

Рассуждая, также как и в предыдущем случае, будем иметь:

И, следовательно:

Если вариации ,инезависимы, то из условия, что, получаем:

Если граничная точка может перемещаться по некоторой кривойи,,, то вариацияили последнее равенство представим следующим образом:

Это условие переходил в следующее:

Отсюда в силу произвольности мы получаем из последнего равенства уравнение:

Это условие название условие трансверсальности для функционала вида:

Условие трансверсальности совместно с уравнениями и, и дает недостающие уравнения для определения произвольных постоянных в общем уравнении системы уравнений Эйлера.

Если граничная точка может перемещаться по некоторой поверхности, то вариация точки имеет вид:

При чем, и- произвольные, следовательно,. Или в развернутом виде:

Последнее равенство преобразуется:

Отсюда, в силу независимости и, получим:

Эти два условия совместно с уравнением дают возможность определить две произвольные постоянные в уравнениях Эйлера.