Уравнения эйлера

Рассмотрим простейший функционал:

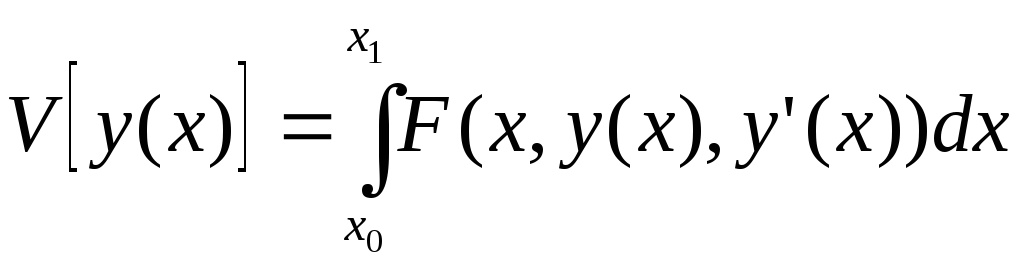(1)

И проведем исследование этого функционала на экстремум. Будем считать, что граничные точки идопустимых кривых заключены. (рис.1)

Подынтегральная функция трижды дифференцируема. Мы уже знаем, что необходимым условием экстремума является обращенная в нуль вариация функционала.

Посмотрим, что даст применение этого условия для исследования данного функционала. Предположим, что экстремум достигается на дважды дифференцируемой кривой , требуя лишь существования производных первого порядка. Заметим какую-нибудь допустимую кривуюи включим кривыеив однопараметрическое семейство кривых:

При получаем, что это есть исходная кривая, а приполучим кривую. (Рис. 2)

Вариации , то естьв вариационных задачах играет роль независимой переменнойдля исследования независимой переменной. Вариация функцииявляется функцией переменной.

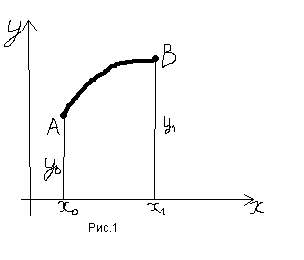
Эту функцию можно дифференцировать сколь угодно раз:

В результате получаем:

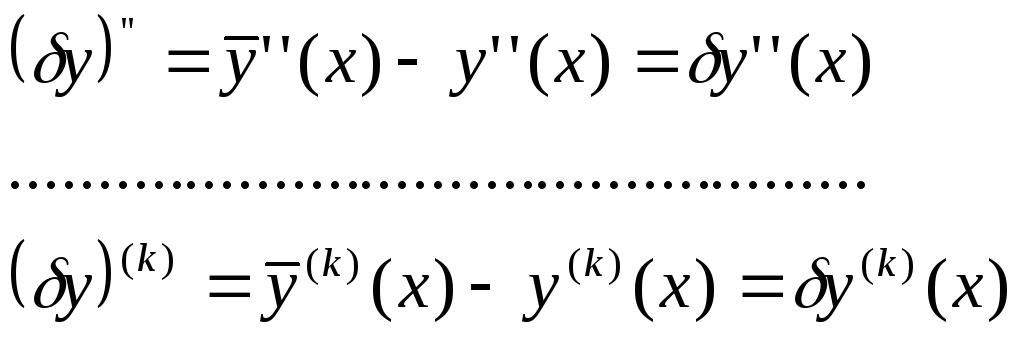
Итак, рассмотрим семейство , где функция семейства определяется следующим выражением:

содержащим параметр , который меняется от 0 до 1.

Если рассмотреть функционал:

только на кривых семейства , то теперь функционал превращается в функцию параметра:

Так как значения параметра определяют кривую, а тем самым определяют и значение функционал. Эта функция достигает своего экстремума приявляется обращением в нуль производной по. То есть когда выполнено условие:.

Берем производную от :

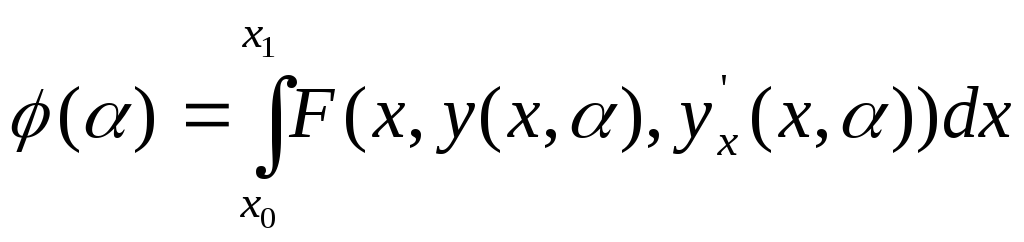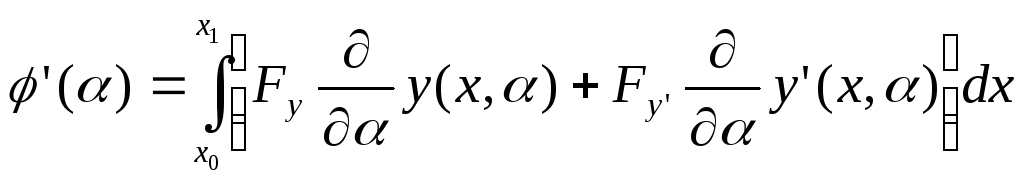
Здесь

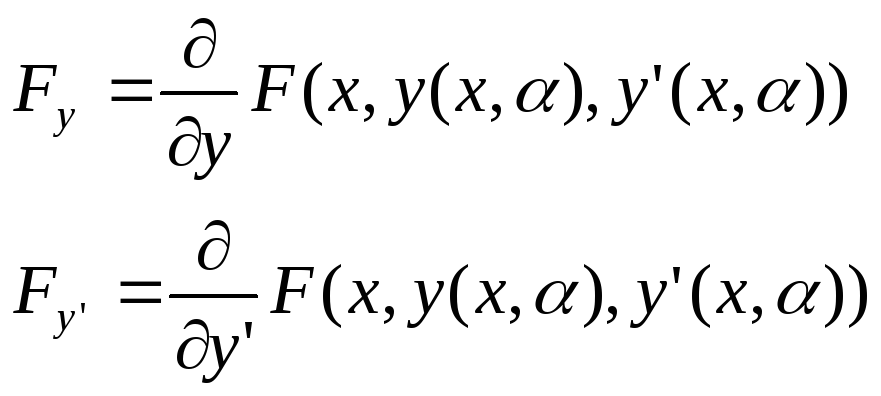
Частная производная по :

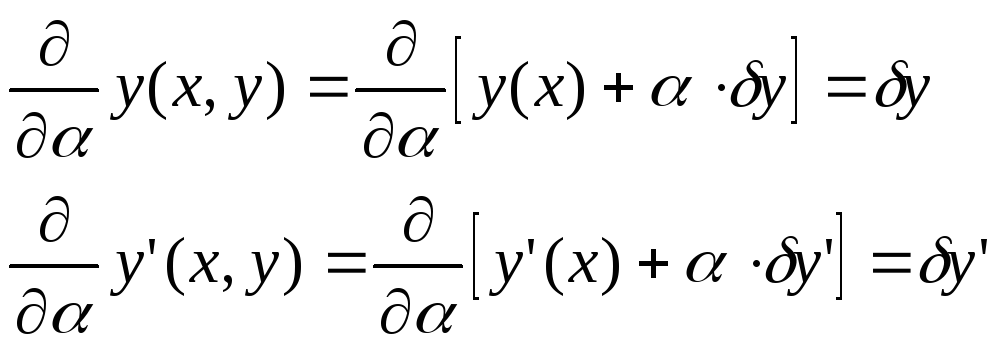
Тогда получается, что определяется следующим равенством:

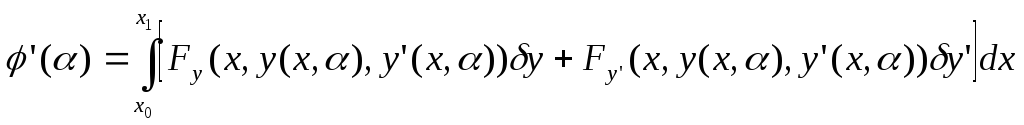
Определяем значение производной в нуле:

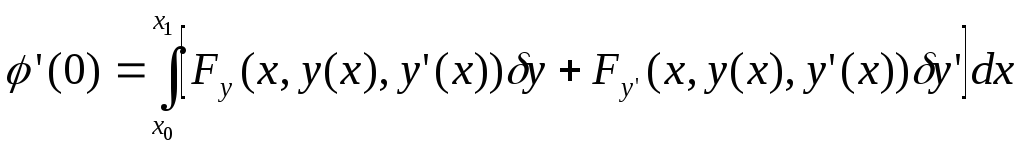
является вариацией функционала, и эту вариацию обозначим. Необходимое условие исследования функционала заключается в обращении в нуль его вариации. Для исходного функционала:

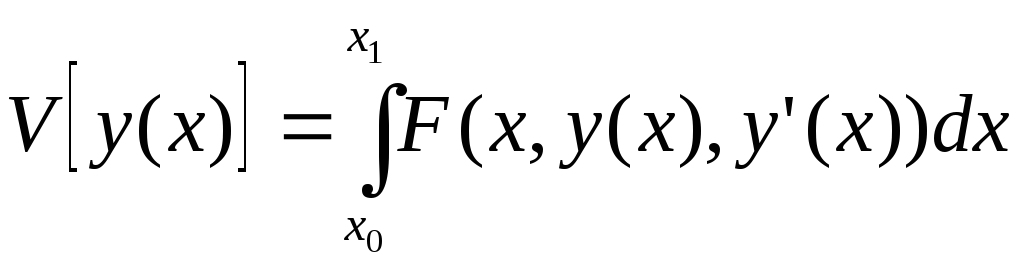
это условие принимает следующий вид:

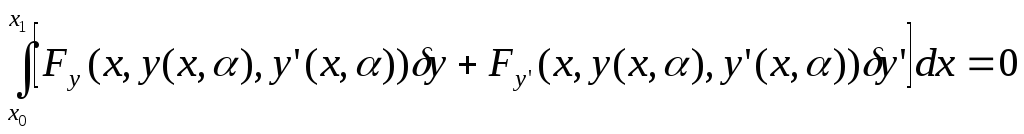
Интегрируя второе равенство по частям и принимая во внимание , получим следующее выражение:

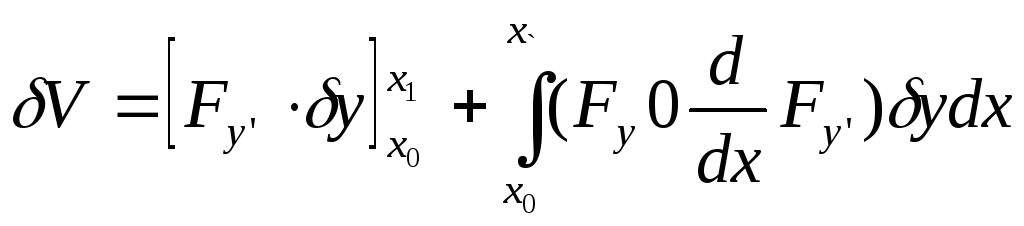
Но

А это значит:

Откуда следует, что граничное условие для этой точки принимает вид:

(2)

При чем первый множитель на кривой, реализующей экстремум является заданной непрерывной функцией.

А второй множитель , ввиду произвола выбора кривой сравнения, является произвольной функцией, которая удовлетворяет лишь некоторым весьма общим уравнениям. Например, функцияв точкахинепрерывна и дифференцируема одним или несколько раз. Для того, чтобы упростить полученный результат, докажем основную лемму вариационного исчисления.

Основная лемма вариационного исчисления

Если для каждой непрерывной функции интеграл, где функциянепрерывна на отрезке, тона этом отрезке.

Утверждение леммы и ее доказательства не изменяются, если на функцию наложить ограничение:.

Доказательство:

Предположим, что в точках , лежащих на отрезке,. Из непрерывности функцииследует, что если, то сама функциясохраняет знак на промежутке. Но тогда, выбрав функцию, также сохраняющую знак в этой окрестности и равную нулю вне этой окрестности.

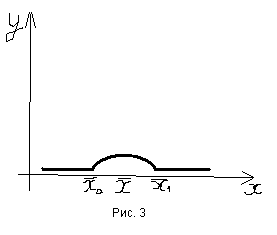
Имеем:

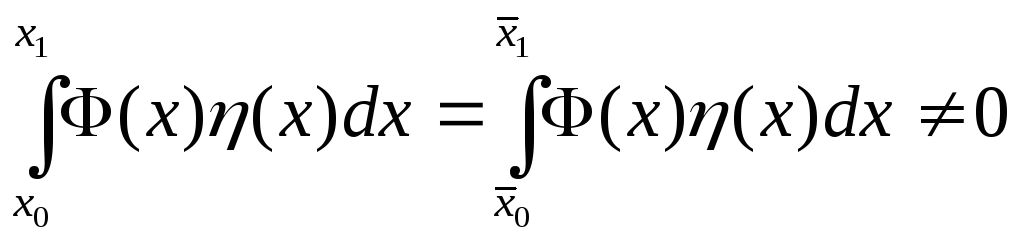
Это справедливо, так как сохраняют знак на промежуткеи обращается в нуль вне этого отрезка.

Мы пришли к противоречию, следовательно . Функциюможно выбирать либо на отрезке, либо следующим образом:

Здесь n– целое положительное число,k– постоянный множитель.

Теперь применим основную лемму вариационного исчисления для упрощения условия (2). Мы ищем условие экстремума для функционала:

Все условия леммы выполнены на кривой, реализующей экстремум. Множитель является непрерывной функцией, а вариацияявляется произвольной функцией, на которую наложены предусмотренные ограничения на кривой общего характера. Следовательно, справедливо уравнение:

В развернутом виде:

Это уравнение было получено Эйлером.

Интегральные кривые , которые являются решением уравнения Эйлера называемые экстремалями. Только на экстремалях может достигаться экстремум функционала:

Для нахождения кривой, реализующей экстремум функционала (1), интегрируем уравнение Эйлера и находим постоянные интегрирования и, входящие в общее решения уравнения, и условия на границеи. Это так называемая краевая задача для дифференциального уравнения.

Только на удовлетворяющим этим условиям экстремалям может реализовываться экстремум функционала. Однако для того, чтобы установить – реален ли на них в действительности экстремум, надо воспользоваться достаточными условиями экстремума.

Краевая задача не всегда имеет решение, Во многих вариационных задачах существование решения очевидно из физического и геометрического смысла задачи. И если решение уравнения Эйлера, удовлетворяющее граничным условиям, единственно, то это единственная экстремаль и будет решением рассматриваемой вариационной задачи.

Рассмотрим некоторые интересные случаи простых задач интегрирования уравнения Эйлера:

Случай 1

Пусть функция не зависит от, то есть правая часть уравнения Эйлера имеет вид:. Это объясняется тем, что.

Решение полученного уравнения не содержит элементов произвола и поэтому не может удовлетворять граничным условиями. Следовательно, решение, рассматриваемое в вариационных задачах, вообще не существует. Лишь в исключительных случаях, когда кривая проходит через граничные условияи. В этом случае может на кривой достигаться экстремум.

Случай 2

Функция линейно зависима от, то есть подынтегральную функцию критерия можно представить следующим образом:

В этом случае функционал запишется следующим образом:

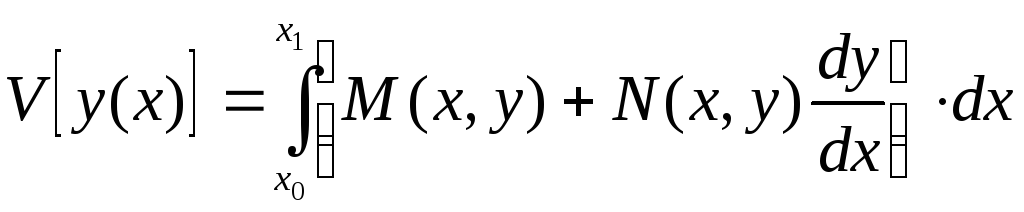
И теперь уравнение Эйлера примет вид:

Это уравнение можно переписать следующим образом:

Эта кривая не удовлетворяет граничным условиям, следовательно, вариационная задача не имеет решения в классе непрерывных функций.

Если выполнено уравнение:

то справедливо равенство:

Тогда это выражение является точным дифференциалом. И тогда функционал:

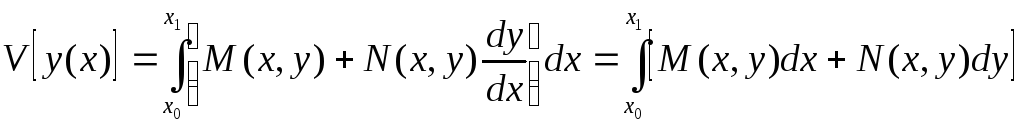
не зависит от пути интегрирования, и его значение постоянно. Следовательно, вариационная задача теряет смысл.

Случай 3

Когда подынтегральная функция в функционале зависит лишь от. То есть подынтегральная функция принимает вид:

А это означает:

Отсюда следует, что и. Отсюда следует, что если, то решение уравнения Эйлера имеет вид:.

Последнее равенство задает двухпараметрическое семейство прямых линий. Если уравнение имеет один или несколько корней, то есть, то его решение определяется следующей формулой, и мы получаем однопараметрическое семейство прямых.

Случай 4

Пусть теперь зависит льи. То есть справедливо равенство:

Уравнение Эйлера в этом случае принимает следующий вид:

а это означает:

То есть это уравнение имеет первый интеграл . При чем, так как полученное уравнение 1 интеграла не содержит, то оно может быть непосредственно проинтегрировано, решив относительнос последовательным интегрированием, или путем введения подходящим образом некоторого параметра.

Случай 5

Функция зависит оти. В этом случае подынтегральная функция функционала имеет вид. Тогда уравнение Эйлера:

Это потому, что справедливо равенство:

Если уравнение Эйлера умножить на , то левая часть уравнения превращается в точный дифференциал:

Действительно:

Первый интеграл уравнения будет иметь вид:

Это уравнение первого порядка не содержит явно независимую переменную , то оно может быть решено либо разрешением относительнои разделения переменных, либо введением некоторого параметра.

Рассмотрим вторую вариацию этого функционала:

По аналогии с правилами дифференцирования можем записать:

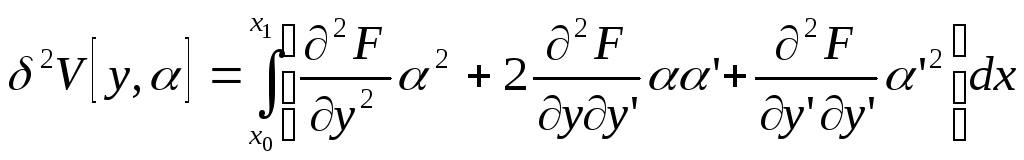(4)

Интегрируя по частям второе слагаемое подынтегральной функции, получаем:

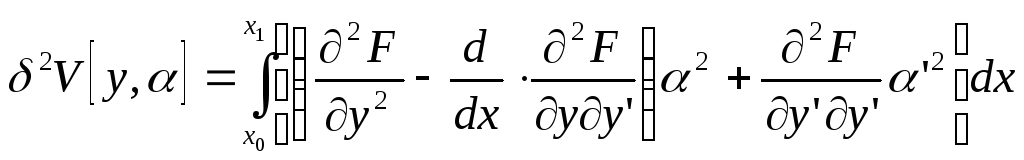(5)

Для того, чтобы функционал 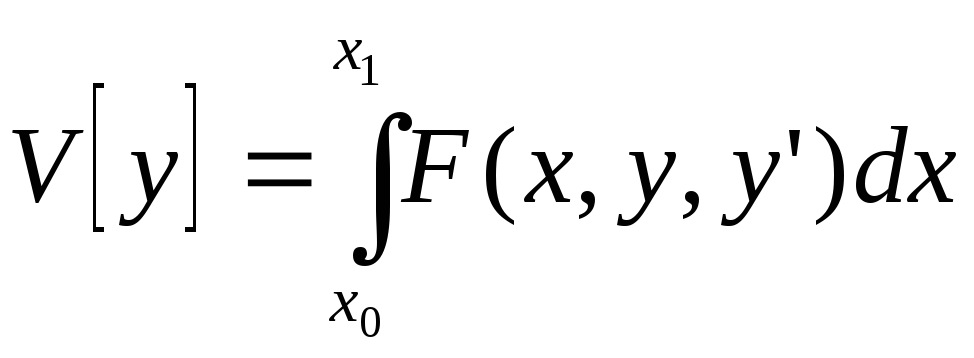в задаче с закрепленными границамиидостигал на кривойэкстремума, необходимо, чтобы вдоль этой кривой выполнялось условие:

- для минимума

(6)

- для максимума

Условия (6) называют условиями Лежандра. Достаточное условие слабого экстремума для простейшей задачи вариационного исчисления формулируется следующим образом:

Для того, чтобы кривая доставляла минимум или максимум функционалу

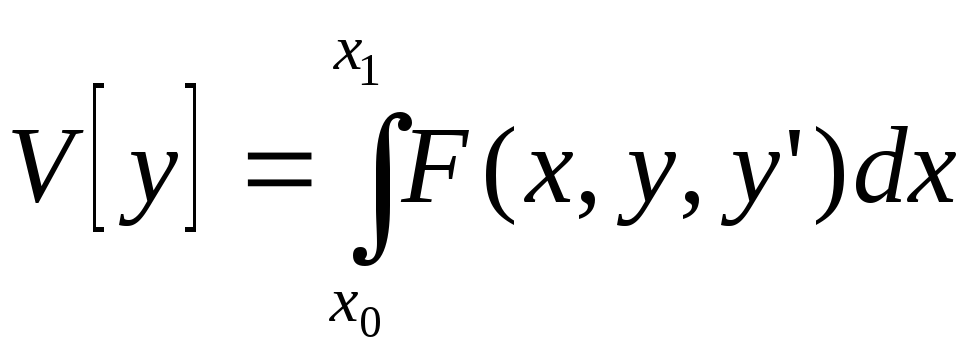
достаточно, чтобы выполнялись условия:

1. Кривая 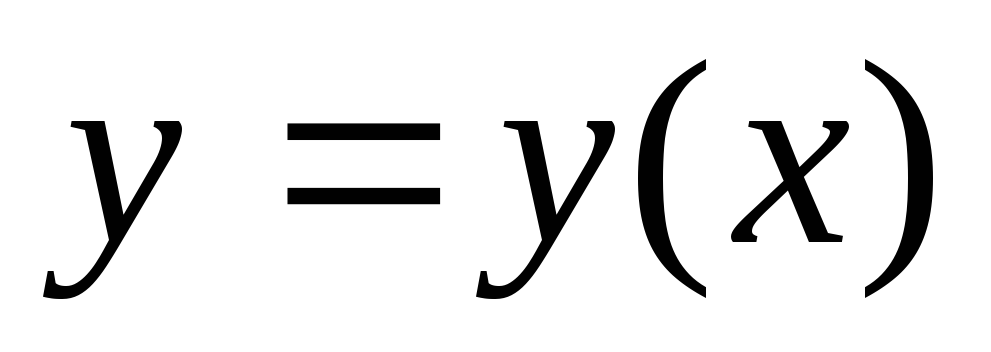была экстремалью, то есть удовлетворяла уравнению Эйлера.

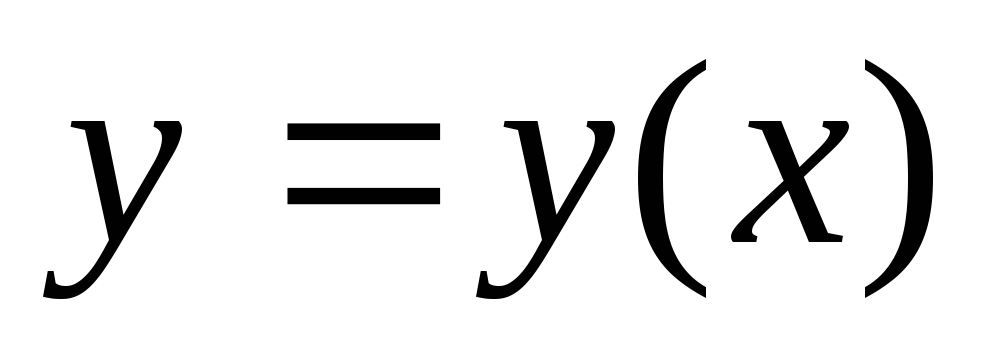2. Вдоль кривой должны иметь место неравенства:

и

3. Уравнение:

(уравнение Якоби) (7)

Здесь:

(8)

на интервале имело решение, не обращающееся в нуль.