Вариационное исчисление

Функционалы– это переменные величины, значения которых определяются выбором одной или нескольких функций.

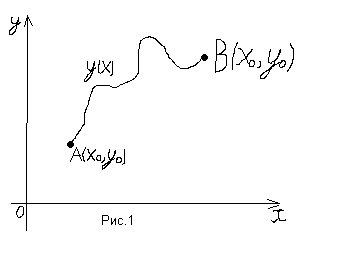
Например, функционалом является длина дуги , которая соединяет две точки (рис.1). Величинаможет быть вычислена, если задано уравнение кривой, тогда длина кривой вычисляется как интеграл:

Площадь Sтакже является некоторым функционалом, так как она определяется выбором функции двух переменных, и вычисляется по формуле:

Здесь D– проекция поверхности на плоскостьOxy.

Вариационное исчисление изучает методы, позволяющие находить максимум и минимум функционалов. Задачи, направленные на нахождение минимума и максимума функционалов называются вариационными.

Задача о брахистохроне

Это задача о быстрейшем спуске из заданной точки А в заданную точку B. Эту задачу предложил Бернулли. И было показано, что наискорейший спуск определяется не по прямой, а по некоторой кривой.

Задача о геодезических линиях

Требуется определить линию наименьшей длины, соединяющую две заданные точки на некоторой поверхности (рис.3).

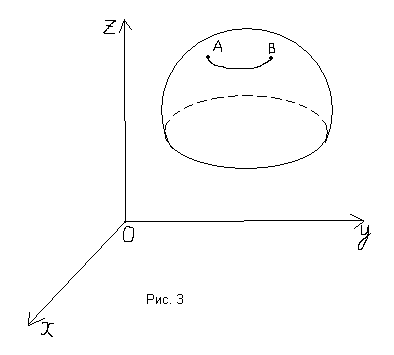
Это типичная задача на условный экстремум. Она формулируется следующим образом:

Требуется найти минимум функционала

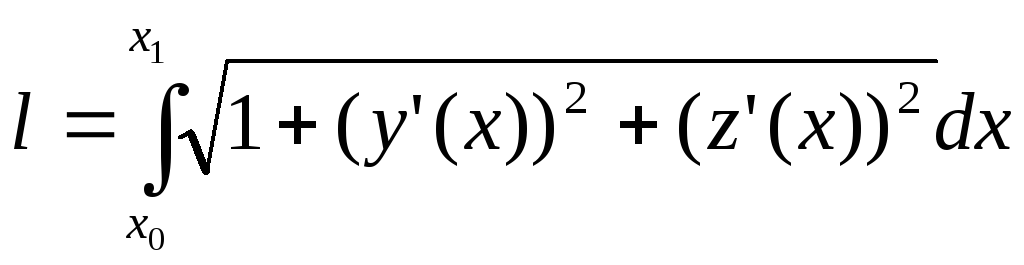
Изопериметрическая задача

Здесь требуется найти замкнутую кривую длины , которая ограничивает максимальную площадьS. И такой линией является окружность.

Здесь требуется определить экстремум функционала .

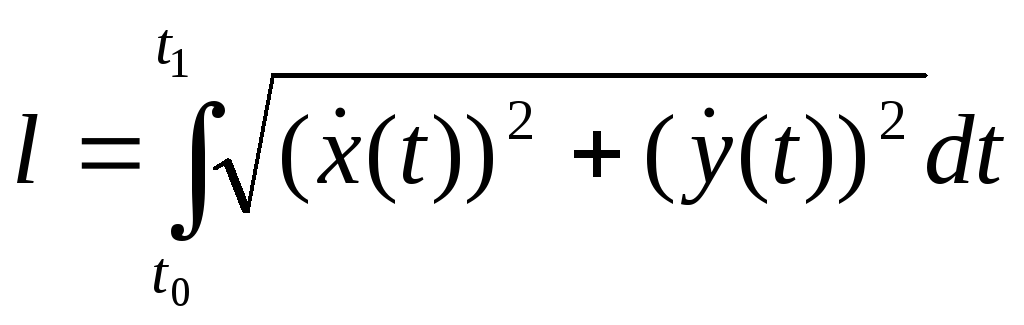Существуют и другие наиболее распространенные виды функционалов:

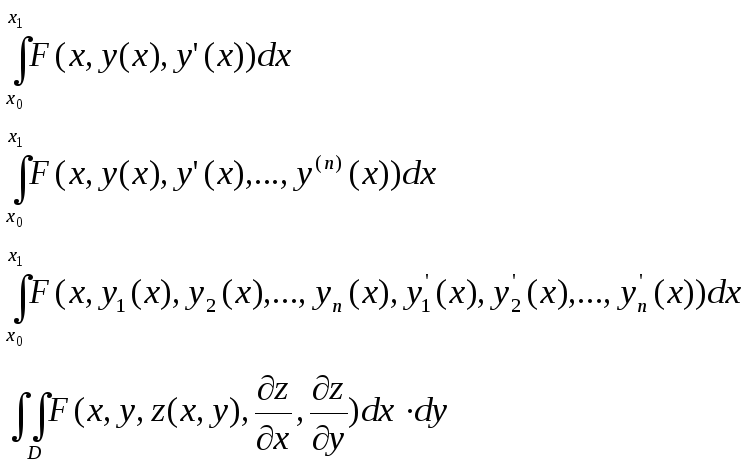
Вариация функционала и ее свойства

Методы решения вариационных задач и поиска экстремума функционала идейно весьма схожи с методами поиска экстремума функции.

1. Переменная величина zназывается функцией переменногоx, если каждой переменной области измененияxсоответствует числуy.

2. Приращением или вариацией аргумента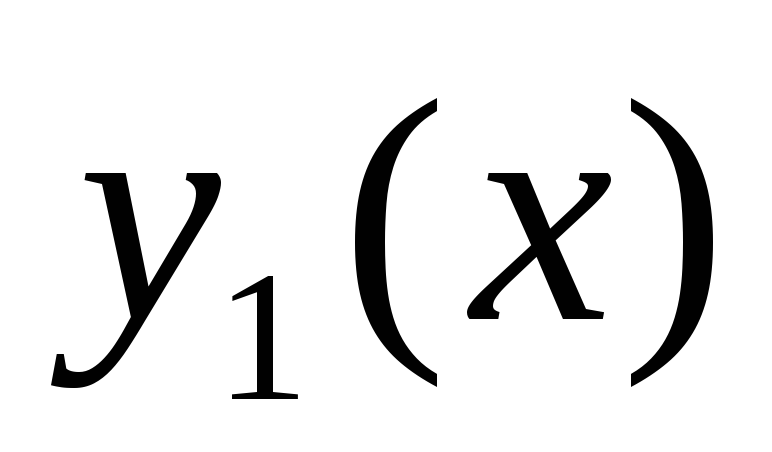функционала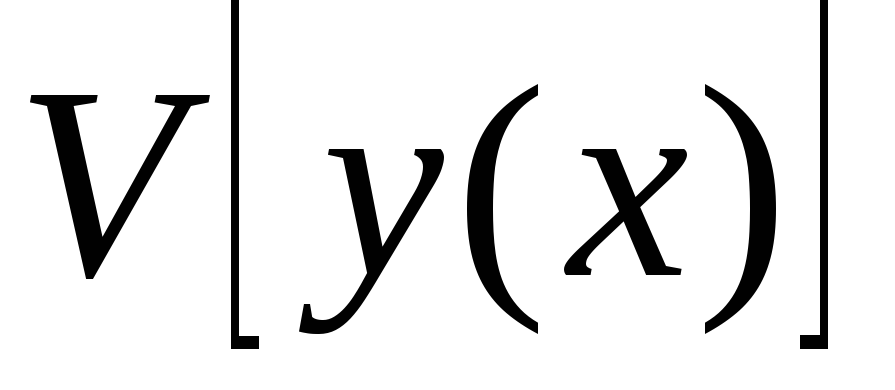называется разность функций. При этом все это рассматривается в некотором классе функций.

3. Функционал называется непрерывным, если малому изменениюсоответствует малое изменение функционала.

Возникает вопрос: какие из двух функций исчитаются мало отличающимися?

Например, можно считать, что эти две функции близки в том случае, если их разность мала для любогоxтам, где эти функции определены.

Функционал вида:

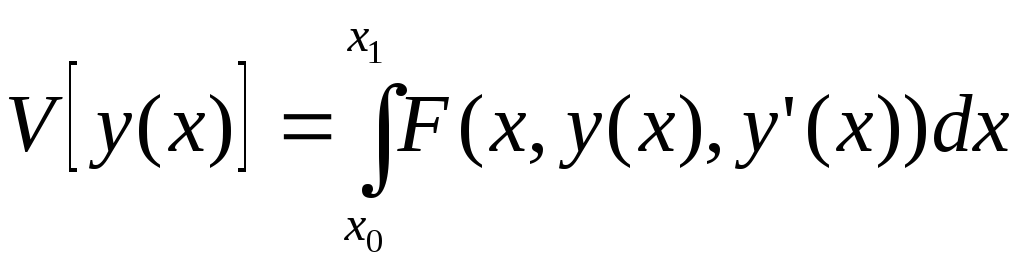
Из за наличия лишь в исключительных случаях будет непрерывным. Поэтому кривые будут близки, если выполняются условия:и. То есть будут близки по своим значениям и производным.

1. Если для двух функци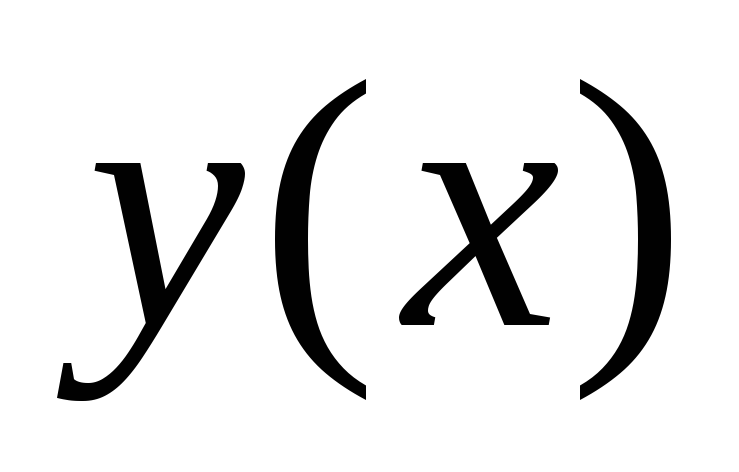й и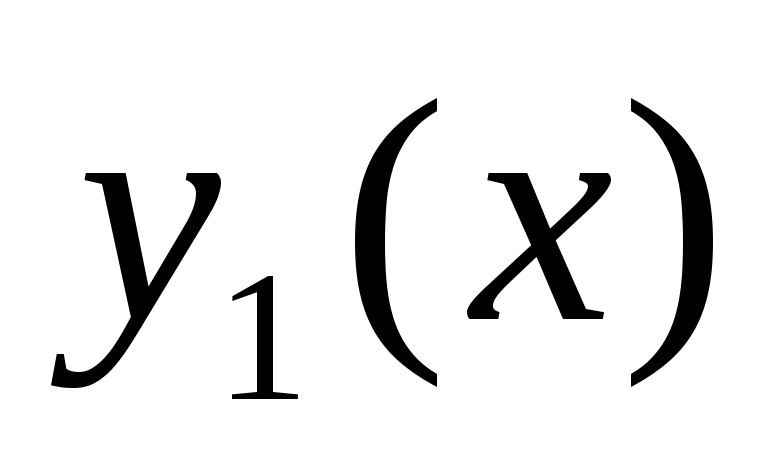разность, то это близостьнулевогопорядка.

2. Если наряду с этим, мала разность их производных , то это близостьпервогопорядка.

3. Когда есть разность kпроизводных, то это близостьk-гопорядка.

На рисунке 4 кривые близки в смысле первого порядка.

На рисунке 5 кривые близки в смысле нулевого порядка.

Функция непрерывная в точке, если для любогоможно подобрать такоеи такое, что модуль разности, когда.

3а. Функционал непрерывен прив смысле близостиk-го порядка, если для любогоможно подобратьтакое, что:

При:

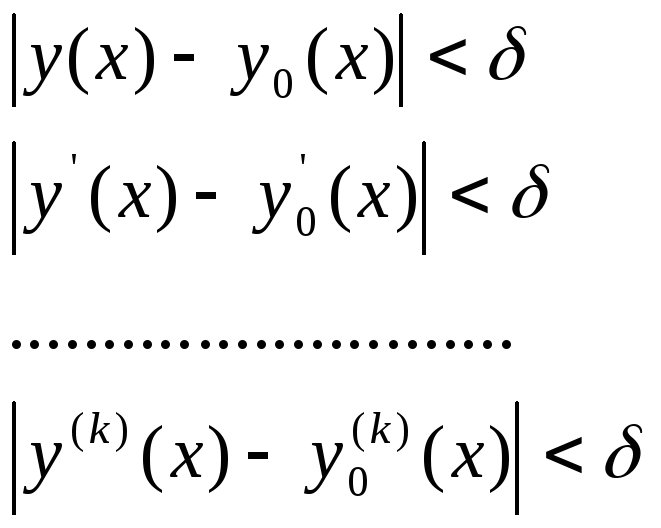
При этом считается, что функционал рассматривается на определенном классе, то есть должен принадлежать определенному классу функций.

Можно ввести в рассмотрение расстояние между двумя функциями , при этом. Тогда близкими можно считать кривые, для которых расстояние между двумя функциями мало. В качестве этого расстояния можно взять величину:

Тогда это будет близость нулевого порядка. Если теперь в качестве расстояния взять величину:

и теперь предположить, что функции необходимое количество раз дифференцируемо, то это близостьk-го порядка.

4. Линейным функционалом называют функционал удовлетворяющий следующим условиям:

Где c– произвольная постоянная.

Пример линейного факториала:

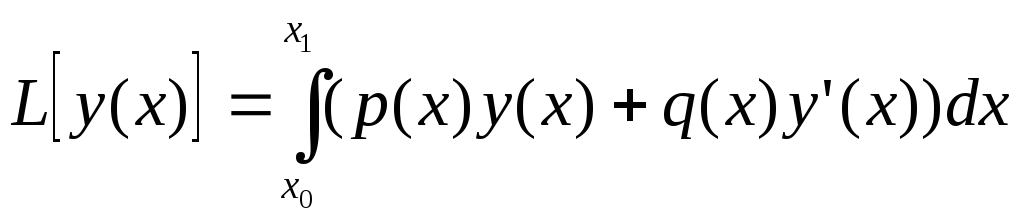
5. Если приращение функционала 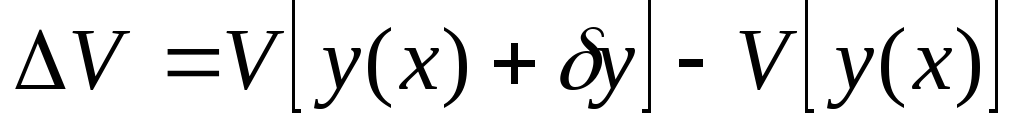можно представить в виде:

Где - линейный по отношению кфункционал;

- максимальное значениеприи, то линейная по отношению кчасть приращение функционала, то есть, называется вариацией функционала и обозначается -.

Вариация функционала – это главная линейная по отношению к часть приращение функционала. При исследовании функционалов вариация играет такую же роль, какую играет дифференциал при исследовании функции. Можно дать и другое, почти эквивалентное определение дифференциала функции и вариации функционала.

Рассмотрим значение функции при фиксированных значенияхи. И пусть только меняется значение. Получим приращение значений функции при изменении. Примы получим.

Если , то.

Производная от функции поприравно дифференциалу функциив точке.

Правило дифференцирования сложной функции:

Это же справедливо и для функции нескольких переменных . Вводится дополнительная переменнаяи ее можно представить следующим образом:

Возьмем производную по :

Рассмотрим функционал и запишем его следующим образом:. А теперь вариацию функционала рассмотрим как производную последнего функционала попри. Если функционал имеет вариацию в смысле главной линейной части приращения, то его приращение будет иметь вид:

Производная функционала по при:

Так как в силу линейности и справедливости равенства:

Следует:

при

Если существует вариация в смысле главной линейной части приращения функционала, то существует и вариация в смысле производной по параметру при начальном значении параметра. И оба эти определения эквиваленты.

Второе определение вариации несколько шире первого, так как существуют примеры функционалов, из приращения которых нельзя выделить главные линейные части. Но вариации в смысле второго определения существуют.

6. Вариация функционала равна.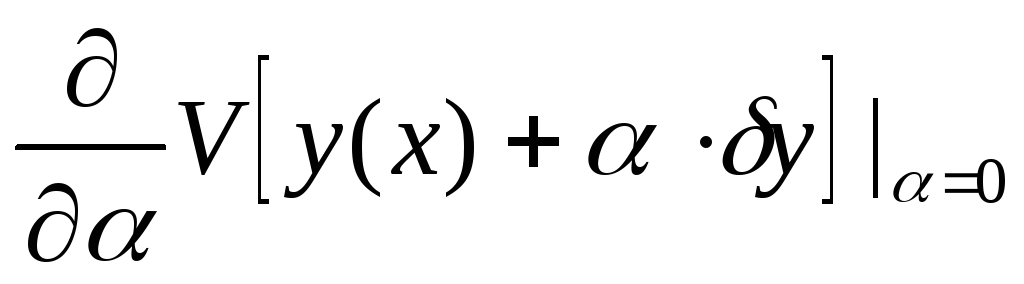

Функционал достигает на кривоймаксимума, если значения функционалана любой близкой кне больше, чем.

То есть:

Если итолько, когда, то говорят, что на кривойдостигается строгий максимум. В этом случае. Таким образом для всех кривых, близких к, справедлива следующая теорема:

Если функционал , имеющий вариацию, достигает максимума или минимума при, где- внутренняя точка области определения функционала, то при.

Доказательство

При фиксированном значении ифункционалявляется функцией параметра, которая припо предположению достигает максимума или минимума.

Следовательно

А это значит, что вариация .

Говоря о максимуме или минимуме, мы имели ввиду наибольшее значение функционала только по отношению к значению функционала на близких кривых. Но как было указано раньше, близость кривых может быть понятна различно. Поэтому в определении максимума или минимума нужно указывать, какого порядка близость имеется ввиду.

Если функционал достигает на кривоймаксимума или минимума по отношению ко всем кривым, для которых модуль разностимал, то есть по отношению к кривымв смысле близости нулевого порядка, то максимум или минимум называется сильным.

Если теперь функционал достигает максимума или минимума лишь в смысле близости первого порядка, то есть по отношению к кривым, близким по направлению к касательным, то максимум или минимум называется слабым.

Если на кривой достигается сильный экстремум, то и подавно достигается слабый экстремум. Если кривыеблизки к кривойв смысле одного и того же порядка. Однако, возможно, что на кривойдостигается слабый максимум или минимум, и в то же время не достигается сильный максимум или минимум. То есть среди кривых, близких к кривым, близких как по координатам, так и по направлениям касательных, может не быть таких, для которых выполняется неравенство:.

А среди кривых , близких по ординате, но уже не близких по направлениям касательных. Здесь могут найтись кривые, для которых может выполнено такое же неравенство.