17. Решение дифференциального уравнения численным методом Эйлера

Решение дифференциального уравнения заключается в нахождении зависимости изменения во времени выходной переменной (рис. 1) при следующих исходных данных:

1. дифференциальное уравнение с параметрами k,Т.

2. начальное значение выходной переменной ,

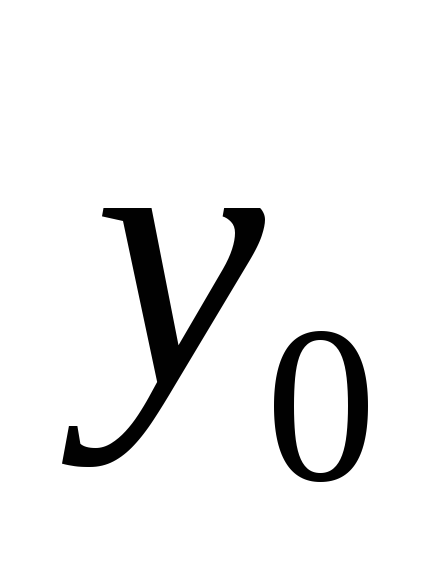3. закон изменения во времени входной переменной .

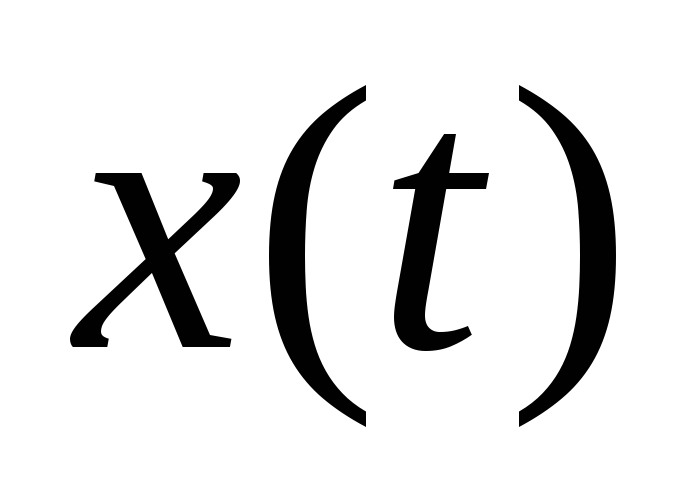При численном решении дифференциального уравнения время берется в дискретные моменты ... Непрерывный входной сигналзаменяется ступенчатым дискретным сигналомПустьесть решение дифференциального уравнения, при начальном значении. Следующее значениеможно определить из треугольника. Суть метода Эйлера заключается в замене криволинейного треугольникаabc(рис. 1) на прямоугольныйabd. Тогда значение выходной переменнойприбудет

Из прямоугольного треугольника abd

,

тогда последующее значение можно определить по его предыдущему

На основании геометрического смысла производной тангенс угла наклона касательной равен значению производной функциив данной точке, которое можно определить по дифференциальному уравнению

. Записывая производную как первую разность, запишем выражение для значенийна основания значенийив предыдущей точке.

Аналогично запишем выражения для всех последующих значений

В общем случае разностное рекуррентное уравнение имеет вид:

Используя данное уравнение, можно последовательно точка за точкой найти решение уравнения первого порядка при заданных , параметрах уравненияи входному сигналу.

18. Операторный метод решения дифференциальных уравнений.

Запишем дифференциальное уравнение n-го порядка

Данное уравнение содержит три величины:

1. Функцию изменения во времени входного сигнала .

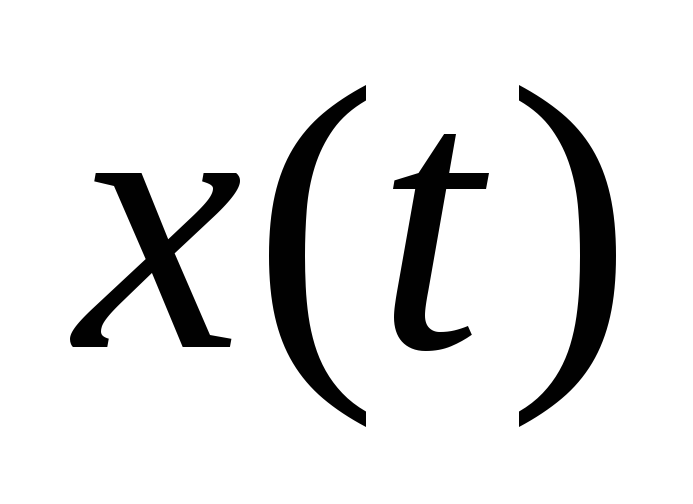2. Функцию изменения во времени выходного сигнала .

3. Само дифференциальное уравнение, являющееся оператором преобразования входной функции времени в выходную функцию времени.

В основе операторного метода решения дифференциальных уравнений лежит преобразование Лапласа. При этом производится перевод переменных из временной плоскости (временные функции и др.) в плоскость комплексной переменной(), что позволяет перевести дифференциальные уравнения связи между переменными в в алгебраические и упростить их решения.

Прямое преобразование Лапласа .

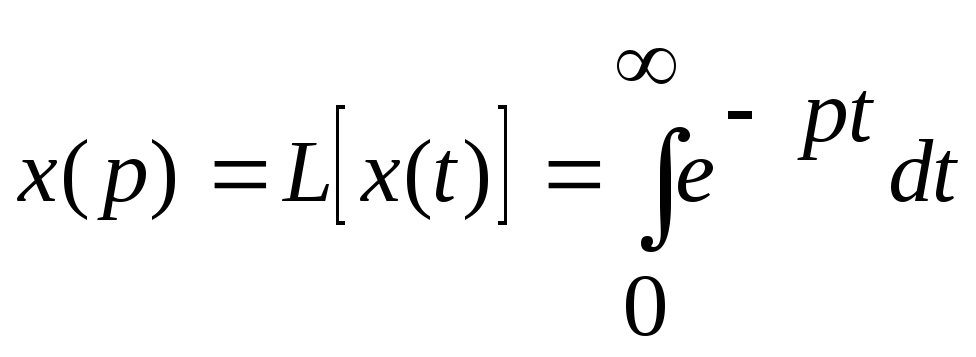называется изображением по Лапласу временной функции

Обратное преобразование Лапласа имеет вид .

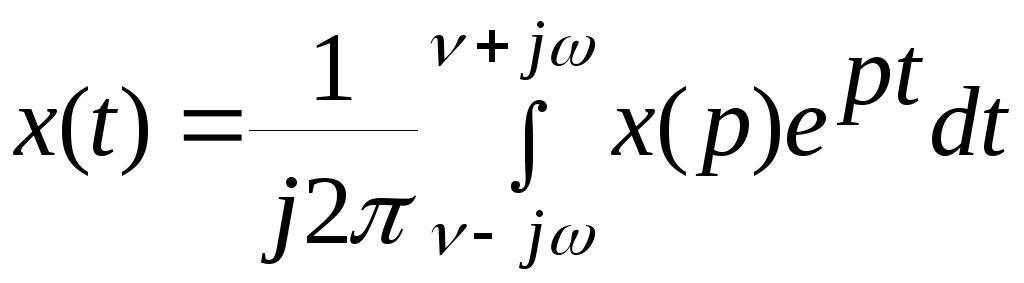Рассмотрим процесс нахождения операторным методом закона изменения выходной переменной динамического звена, описываемого дифференциальным уравнением ДУ при законе изменения входной переменной(см. рис. ). Алгоритм решения задачи символическим методом заключается в следующем:

1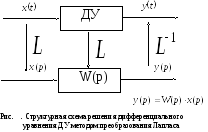. Записывается дифференциальное уравнение, описывающее закономерности рабаты динамического звена.

2. Делается преобразование дифференциального уравнения по Лапласу:

1) вместо записываются функции комплексной переменной,

2) производные выражаются через оператор , а именно,и т.д., напримери т.д. При этом вместо дифференциального уравнения получается алгебраическое. Таким образом, умножение в комплексной плоскости на опереторозначает, что во временной плоскости производится дифференцирование. И, соотвественно, деление в компексной плоскости на операторозначает обратное действие - интегрирование.

3. Делается преобразование Лапласа от закона изменения входной переменной . Для этого существуют таблицы преобразования Лапласа в справочниках, а также команды символьных преобразований в математических процессорах компьютеров.

4. Полученное алгебраическое уравнения решается относительно

5. Делается обратное преобразование Лапласа от и получается искомое решение- закон изменения во времени выходной переменной.

19. Передаточная функция элемента системы управления.Преобразование Лапласа дифференциального уравнения приводит к удобному и широко применяемому выражению связи между изображениями входной и выходной величин через передаточную функцию. Преобразуем по Лапласу анализиуемое дифференциальное уравнение

В правой и левой частях выражения появились множители y(p)и, которые можно вынести за скобки

Запишем отношение

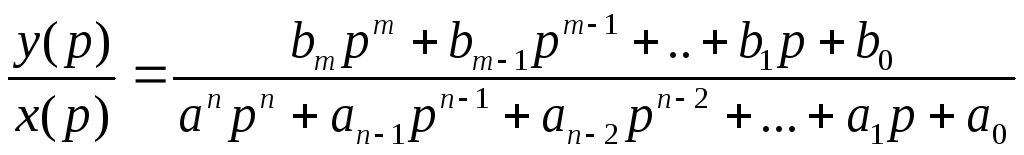
Отношение изображения выходной величины звена (системы) к изображению входной величины называется передаточная функцияи обычно обозначается. В данном случае

Изображение выходной переменной находится как произведение произведение передаточной функции на изображение входной переменной,

что существенно упрощает анализ элементов и систем управления.

Передаточная функция обычно имеет вид правильной рационалной дроби в виде отношений полиномов от оператора Лапласа p(в литературе также часто используется обозначение ).. Степень полиномаР(р)больше или равна степени полиномаQ(p)из условия физической реализуемости, которая означает, что сигнал на выходе не может появиться раньше появления сигнала на входе. Коэффициентыa_iиb_iвещественные числа. Корни характеристического уравнения - называются полюсами системы. КорниQ(р)=0- называются нулями системы.

Вид решения (график выходной переменной) зависит от вида полюсов и нулей передаточной функции. Они могут быть вещественные, нулевые, комплексные с положительной или отрицательной вещественной связью. Если определить все полюса и нули системы и нанести их на комплексную плоскость, получим точки, размещенные в определенном месте этой плоскости. Исходя из их положения можно сделать анализ системы.

Таким образом, имеется связь между комплексными переменными и решением уравнения во временной плоскостями. Положение полюсов и нулей на комплексной плоскости определяет вид графика y(t)во временной плоскости.