
- •60 Вопросов 60 ответов
- •1. Алгоритм работы системы управления с отрицательной обратной связью.
- •2. Функциональная схема. Основные элементы систем управления
- •3. Структурная схема системы управления. Сигналы, действующие в системах
- •4. Входы, выходы систем управления
- •5. Назначение систем управления
- •6. Функциональный, структурный анализ системы управления
- •7. Примеры систем управления
- •8. Классификация систем управления
- •9. Типовые модели детерминированных сигналов
- •17. Решение дифференциального уравнения численным методом Эйлера
- •18. Операторный метод решения дифференциальных уравнений.
- •20. Получение передаточных функций из дифференциальных уравнений.
- •22. Линеаризация статических и динамических характеристик.
- •23. Статические и динамические характеристики элементов (системы)
- •24. Статическая характеристика. Статические, астатические элементы.
- •25. Временные характеристики динамических звеньев
- •26. Частотные характеристики динамических звеньев
- •27. Логарифмические частотные характеристики.
- •28. Дифференциальное уравнение n-го порядка. Модели основных типовых звеньев.
- •29. Усилительное звено. Математическая модель, характеристики.
- •30. Апериодическое звено первого порядка. Математическая модель, характеристики.
- •31. Интегрирующее звено. Математическая модель, характеристики.
- •32. Дифференцирующее звено. Математическая модель, характеристики.
- •33. Звено второго порядка. Математическая модель, характеристики.
- •34. Эквивалентные модели последовательного, параллельного, встречно-параллельного соединений элементов системы управления.
- •18. Виды передаточных функций системы управления, их определение по передаточным функциям элементов системы.
- •20. Анализ ошибок системы при различных законах изменения задающего воздействия.
- •19. Методы разработки систем управления.
- •Классический метод решения дифференциальных уравнений:
- •1. Упрощение временных функций.
- •3) Обратное преобразование Лапласа.
22. Линеаризация статических и динамических характеристик.
З акономерности
работы элементов системы в общем случае
являются нелинейными, что существенно
усложняет анализ работы систем. Однако
при эффективно работающих системах
диапазон изменения переменных объекта
небольшой, что позволяет упростить
анализ систем управления путем перехода
к описанию закономерностей линейными
уравнениями. Это поясняется графиком
на рис. . На графике видно, что при
измененииxв диапазоне
акономерности
работы элементов системы в общем случае
являются нелинейными, что существенно
усложняет анализ работы систем. Однако
при эффективно работающих системах
диапазон изменения переменных объекта
небольшой, что позволяет упростить
анализ систем управления путем перехода
к описанию закономерностей линейными
уравнениями. Это поясняется графиком
на рис. . На графике видно, что при
измененииxв диапазоне![]() нелинейная зависимость
нелинейная зависимость![]() может быть аппроксимирована линейным
уравнением
может быть аппроксимирована линейным
уравнением![]() .
Но значения коэффициентов линейного
уравнения зависят от места нахождения
рабочей точки на
.
Но значения коэффициентов линейного
уравнения зависят от места нахождения
рабочей точки на![]() .
.
Таким образом, нелинейную систему можно анализировать как линейную, что очень распространено в теории управления при малых отклонениях от рабочей точки.
Методы линеаризации.
1. Метод разложения в ряд Тейлора.
Из курса математики известно, что любую
функцию в окрестности точки
![]() можно с большой точностью разложить в
ряд Тейлора:
можно с большой точностью разложить в
ряд Тейлора:
![]()
При оставлении одного члена ряда функция
аппроксимируется уравнением прямой
![]()
В качестве примера найдем линейную
аппроксимацию для квадратичной функции
качестве примера найдем линейную
аппроксимацию для квадратичной функции
y=2x2
![]()
При x0=2 f(x)=8+8x
При x0=4 f(x)=32+16x
М
 етод
наименьших квадратов. При узком
диапазоне изменения переменных
линеаризация путем использования
уравнения касательной (ряд Тейлора)
достаточно точен, но для выпуклой/вогнутой
кривой все линеаризованные значения
лежат выше/ниже фактических, что
дает ошибку существенную при больших
изменениях диапазона, поэтому часто
используют метод наименьших квадратов
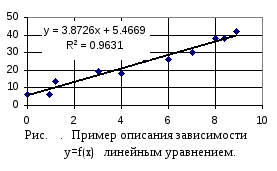
МНК. Примем описания зависимости
етод
наименьших квадратов. При узком
диапазоне изменения переменных
линеаризация путем использования
уравнения касательной (ряд Тейлора)
достаточно точен, но для выпуклой/вогнутой
кривой все линеаризованные значения
лежат выше/ниже фактических, что
дает ошибку существенную при больших
изменениях диапазона, поэтому часто
используют метод наименьших квадратов
МНК. Примем описания зависимости в рабочем диапазоне измененияxуравнением прямой линии в электронных
таблицахExcelприведен на
рис. .
в рабочем диапазоне измененияxуравнением прямой линии в электронных
таблицахExcelприведен на
рис. .
Линеаризация дифференциальных
уравнений.Линеаризацию дифференциальных
уравнений рассмотрим на примере
построения математической модели.
Имеется реактор с мешалкой. На входе
реактора два потока: первый - химический
реагент с расходом и концентрацией![]() ,
второй поток - вода с расходом в единицу
времени
,
второй поток - вода с расходом в единицу
времени![]() ,
на выходе один поток с расходом и
концентрацией
,
на выходе один поток с расходом и
концентрацией![]() (рис. 5).
(рис. 5).
Расходы на входе и концентрация первого
потока могут изменяться. Построить
математическую модель объекта управления
в виде дифференциального уравнения и
передаточные функции входных переменных
![]() на концентрацию на выходе
на концентрацию на выходе![]()
 Объект
управления имеет три входа и один выход
(рис 5 б).
Объект
управления имеет три входа и один выход
(рис 5 б).



В системах стабилизации устанавливается
статический режим. В системах
программного управления, следящих
системах координаты системы должны
изменяться по заданному закону
![]() но из-за действующих возмущающих
воздействий данные координаты смещаются
от заданных значений. Зависимости,
описывающие их движения, также могут
быть нелинейными. Но так как при
эффективной работе систем управления
отклонения невелики, то зависимости
можно линеаризовать. Можно производить
линеаризацию отдельных звеньев и
систем.
но из-за действующих возмущающих
воздействий данные координаты смещаются
от заданных значений. Зависимости,
описывающие их движения, также могут
быть нелинейными. Но так как при
эффективной работе систем управления
отклонения невелики, то зависимости
можно линеаризовать. Можно производить
линеаризацию отдельных звеньев и
систем.
Используют метод разложения в ряд
Тейлора. Пусть уравнение системы
![]() Еслиf=f0,u=u0,
то после окончания переходного
процесса система придет в установившееся
состояние, т.е. в статический режим.
Еслиf=f0,u=u0,
то после окончания переходного
процесса система придет в установившееся
состояние, т.е. в статический режим.
Система программного управления.
![]()
![]()
![]() .
Задана траектория движения системы.
.
Задана траектория движения системы.
Уравнение движения системы в отклонениях
от заданной траектории:![]() .
.![]() Подставим переменные в исходные
уравнения и запишем:
Подставим переменные в исходные
уравнения и запишем:
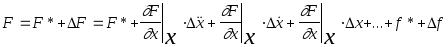
![]()
![]()
Линейное уравнение, описывающие отклонения координат системы от заданной траектории. Если время tявно не входит в уравнение (имеется ввиду не производная, а напримерк0(t)) и коэффициенты не зависят отt, то имеем линейное дифференциальное уравнение с постоянными коэффициентами. Это самый простой случай, но имеет частое применение для полного анализа системы или как первый шаг ее анализа. Далее система может усложняться путем ввода новых факторов, которые на первом этапе были отброшены.
Запишем уравнение линеаризации системы:
1) u, x 0.
2) F(x,u,f)обладает непрерывными частными производными по всем аргументам.
Пример: составим уравнение движения электродвигателя.
![]()
 ,
,
![]() - нелинейные
- нелинейные
![]() функции
функции
![]()
Линеаризуем нелинейные функции:
![]()
![]()
![]()
Уравнение в статике
![]() ,
,![]()
![]() ,uu.
,uu.
![]()
Математические модели в пространстве состояния.
Системы управления и их элементы описываются различными математическими моделями:
-дифференциальными уравнениями,
- передаточными функциями,
- временными характеристиками,
- частотными характеристиками и др.
Модели различных систем имеют различный порядок и различную структуру и поэтому методы их решения также изменяются.
Важно иметь модель, вид которой для различных систем не изменяется и метод решения может быть единым. Такой моделью является математическая модель в пространстве состояния.
Это фактически запись дифференциального уравнения элемента или системы в виде системы уравнений первого порядка, т.е. в форме Коши.
Модель в пространстве состояния имеет вид
![]() Здесь первое уравнения – уравнение
состояния системы, второе – уравнение
выхода.
Здесь первое уравнения – уравнение
состояния системы, второе – уравнение
выхода.
Здесь: X– вектор размерностьюnпараметров состояния системы, это внутренние параметры объекта управления, определяющие его состояние.
U– вектор размерностьюr управляющих параметров системы,
Y- вектор размерностьюmнаблюдаемых параметров системы, это параметры объекта управления, которые измеряются с помощью датчиков и других систем контроля,
A– матрица
размерностью![]() ,
взаимосвязи параметров состояния,
,
взаимосвязи параметров состояния,
B– матрица размером![]() связи параметров состояния с управляющими
параметрами,
связи параметров состояния с управляющими
параметрами,
C– матрица размером![]() связи выходных параметров с параметрами
состояния,
связи выходных параметров с параметрами
состояния,
D- матрица размером![]() связи выходных параметров с управляющими
параметрами.
связи выходных параметров с управляющими
параметрами.
Рассмотрим построение модели состояния из дифференциального уравнения системы.
Пусть система 3-го порядка описывается дифференциальным уравнением
![]()
Запишем данное уравнение относительно старшей производной
![]()
![]()
Введем переменную
![]() ,
обозначим
,
обозначим![]()
Тогда уравнение системы можно записать
в виде
![]()
Обозначим
![]()
Мы получили систему трех уравнений первого порядка
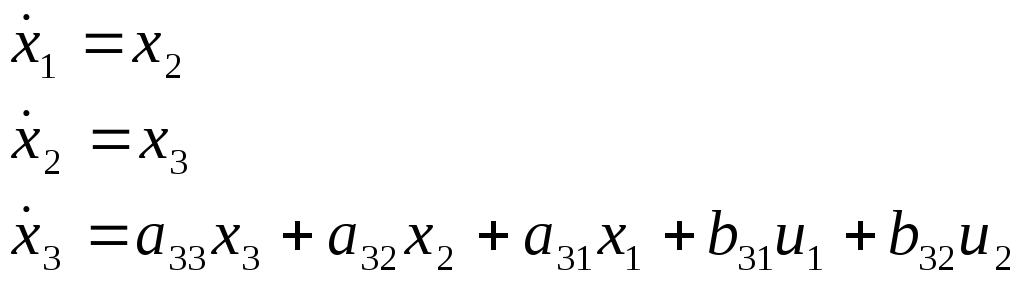
Запишем данную систему уравнений в матричном виде

Обозначив
![]() ,
,![]() ,
,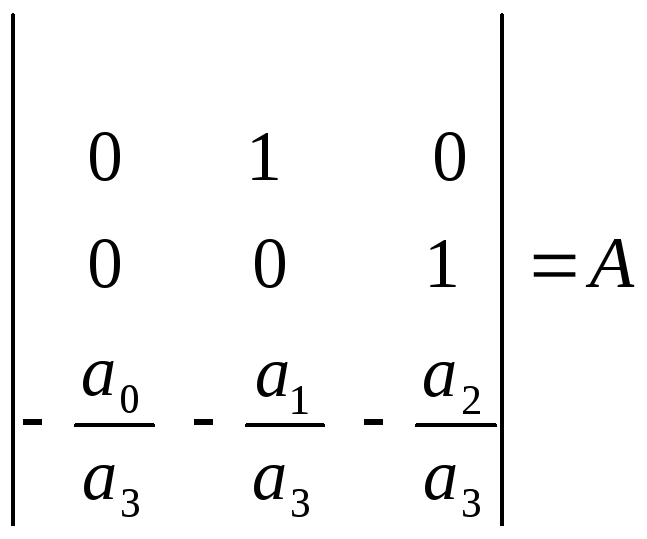 ,
,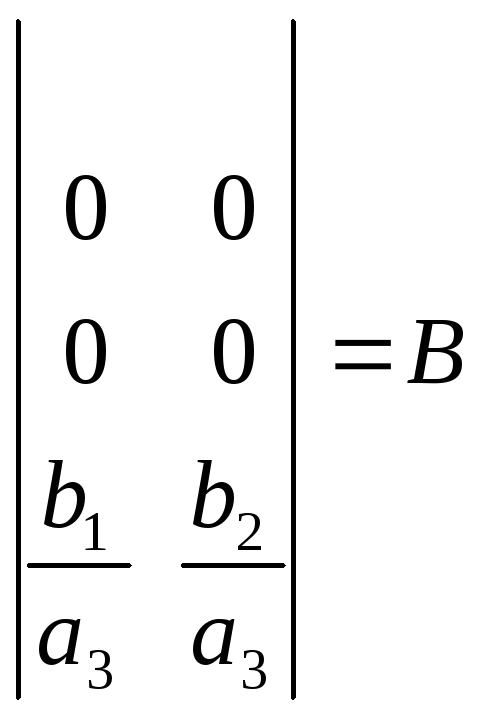 ,
,
Можно данную систему уравнений записать
в матричном виде
![]()
Пусть измеряется выходная переменная
![]() .
Тогда уравнение выхода будет иметь вид
.
Тогда уравнение выхода будет иметь вид
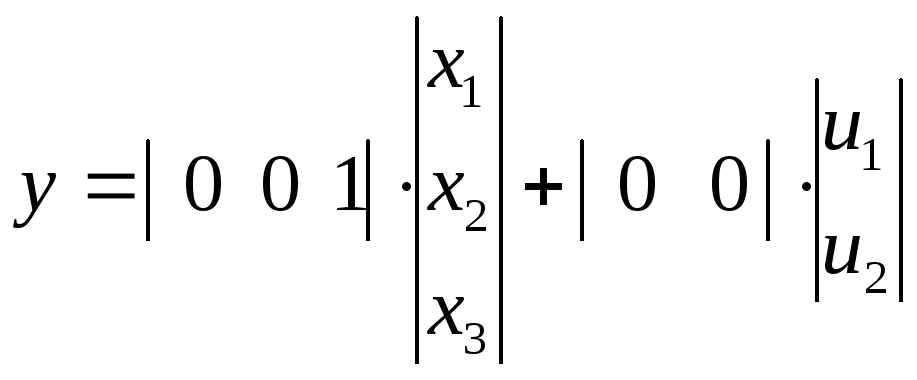 .
Обозначив
.
Обозначив![]() ,
перепишем уравнение выхода в виде
,
перепишем уравнение выхода в виде![]()
Мы получили классическое уравнение системы в пространстве состояния
![]()
Структурная схема модели, построенная на основании матричных уравнений имеет вид
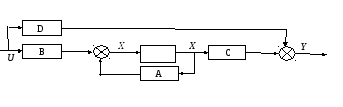
При решении технических задач различного вида и сложности при использовании данной модели будут изменяться только размеры и элементы соответствующих матриц и векторов, а структура модели и методы анализа не изменяются. Для анализа систем используется пакет анализа ControlSystemToolboxсистемыMatLab.
Примеры построения уравнений состояния рассматриваются в следующих вопросах.
Построение модели Коши двойного интегрирующего звена.
Передаточная функция двойного интегрирующего звена имеет вид:
![]()
Дифференциальное уравнение будет
![]()
Обозначим переменную
![]() и запишем уравнение второго порядка в
виде системы двух уравнений в форме
Коши
и запишем уравнение второго порядка в
виде системы двух уравнений в форме
Коши
![]()
Мы получили математическую модель двойного интегрирующего звена в форме Коши.
Построение модели Коши реального интегрирующего звена.
Передаточная функция реального интегрирующего звена имеет вид:
![]()
Дифференциальное уравнение будет
![]()
Перепишем уравнение, оставив в левой части только старшую производную,
![]()
Обозначим переменные
![]() и запишем уравнение второго порядка в
виде системы двух уравнений в форме
Коши
и запишем уравнение второго порядка в
виде системы двух уравнений в форме
Коши
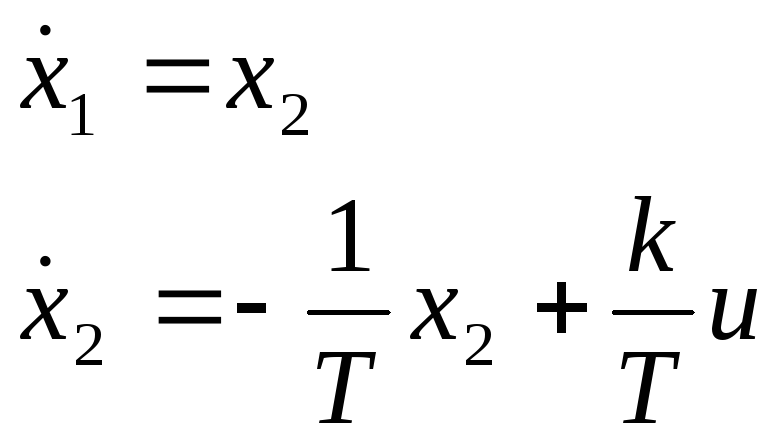
Мы получили математическую модель реального интегрирующего звена в форме Коши.
Построение модели Коши апериодического звена второго порядка.
Передаточная функция реального интегрирующего звена имеет вид:
![]()
Дифференциальное уравнение будет
![]()
Перепишем уравнение, оставив в левой части только старшую производную,
![]()
Обозначим переменную
![]() и запишем уравнение второго порядка в
виде системы двух уравнений в форме
Коши
и запишем уравнение второго порядка в
виде системы двух уравнений в форме
Коши

Мы получили математическую модель реального интегрирующего звена в форме Коши.
