
- •60 Вопросов 60 ответов
- •1. Алгоритм работы системы управления с отрицательной обратной связью.
- •2. Функциональная схема. Основные элементы систем управления
- •3. Структурная схема системы управления. Сигналы, действующие в системах
- •4. Входы, выходы систем управления
- •5. Назначение систем управления
- •6. Функциональный, структурный анализ системы управления
- •7. Примеры систем управления
- •8. Классификация систем управления
- •9. Типовые модели детерминированных сигналов
- •17. Решение дифференциального уравнения численным методом Эйлера
- •18. Операторный метод решения дифференциальных уравнений.
- •20. Получение передаточных функций из дифференциальных уравнений.
- •22. Линеаризация статических и динамических характеристик.
- •23. Статические и динамические характеристики элементов (системы)
- •24. Статическая характеристика. Статические, астатические элементы.
- •25. Временные характеристики динамических звеньев
- •26. Частотные характеристики динамических звеньев
- •27. Логарифмические частотные характеристики.
- •28. Дифференциальное уравнение n-го порядка. Модели основных типовых звеньев.
- •29. Усилительное звено. Математическая модель, характеристики.
- •30. Апериодическое звено первого порядка. Математическая модель, характеристики.
- •31. Интегрирующее звено. Математическая модель, характеристики.
- •32. Дифференцирующее звено. Математическая модель, характеристики.
- •33. Звено второго порядка. Математическая модель, характеристики.
- •34. Эквивалентные модели последовательного, параллельного, встречно-параллельного соединений элементов системы управления.
- •18. Виды передаточных функций системы управления, их определение по передаточным функциям элементов системы.
- •20. Анализ ошибок системы при различных законах изменения задающего воздействия.
- •19. Методы разработки систем управления.
- •Классический метод решения дифференциальных уравнений:
- •1. Упрощение временных функций.
- •3) Обратное преобразование Лапласа.
9. Типовые модели детерминированных сигналов
1. Модели детерминированных сигналов.
С качкообразное
воздействие величиной А:x(t)=
качкообразное
воздействие величиной А:x(t)=![]() .
Здесь
.
Здесь![]() - единичная функция Хевисайда.
- единичная функция Хевисайда.![]()
И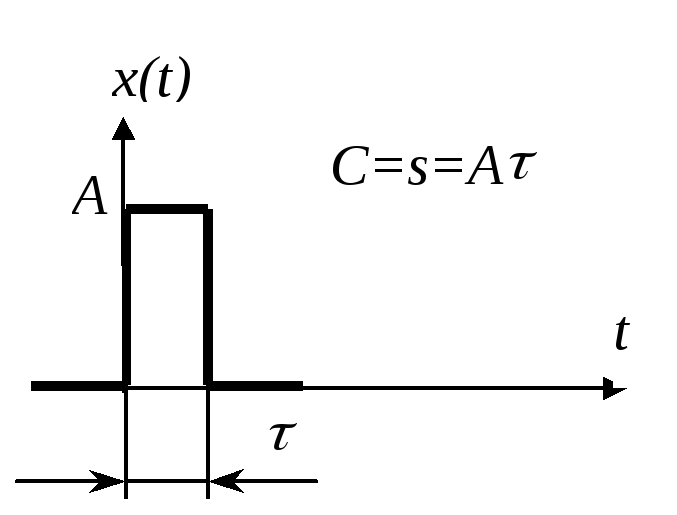 мпульсное
воздействие. Во
временной области импульсное воздействие
характеризуется амплитудой А
и продолжительностью
импульса. Математически ипульс
характеризуется площадью
мпульсное
воздействие. Во
временной области импульсное воздействие
характеризуется амплитудой А
и продолжительностью
импульса. Математически ипульс
характеризуется площадью
![]() и описывается импульсивной функцией
и описывается импульсивной функцией![]() - с импульсом С. Здесь
- с импульсом С. Здесь![]() - дельта - функция Дирака.
- дельта - функция Дирака.
![]() и
и![]()
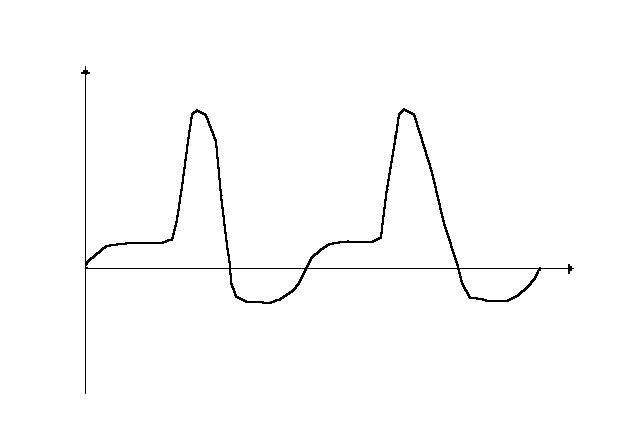
4 Гармонические процессы - сигналы, содержащиеодну гармонику (например: синусоидальный периодический процесс.
![]() ;
;![]() ,
Период
,
Период![]() .
.
 5
Полигармонические процессы - периодические
несинусоидальные процессыx(t)=x(t+n·T)
5
Полигармонические процессы - периодические
несинусоидальные процессыx(t)=x(t+n·T)
Такие процессы являются суммой гармоник, выявление которых производится разложением сигнала в ряд Фурье.
а) Разложение на сумму синусоид и косинусоид:
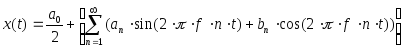
![]() ,
,![]() .
.
б) Разложение на ряд сдвинутых по фазе синусоид:
![]() ;
;![]() ,
,
![]() ,
,![]() , n=1,
2, ...
, n=1,
2, ...
10. Характеристики случайных сигналов
Для работы со случайными процессами наиболее широко используются следующие пять характеристик:
1) математическое ожидание
![]() ;
;
2) дисперсия
![]() ;
;
3) дифференциальная и интегральная
функции распределения
![]() ;
;
4) корреляционная функция
![]() ;
;
5) спектральная плотность
![]() ;
;
При анализе следует различать генеральную совокупностьслучайной величины, представляющую собой все возможные значения данного параметра за все время работы анализируемого процесса, и так называемуювыборку случайного процесса, представляющую собой конкретные значения (график) случайной величины, например, за текущие сутки.
Н азванные
выше характеристики случайных процессов
являютсятеоретическими характеристиками,
описывающими все множество случайных
процессов (генеральную совокупность).
Их значения получить сложно и на практике
пользуются ихоценками, полученными
на основании экспериментальных выборок,
являющихся частью генеральных
совокупностей случайной величины.
Условно говоря,оценкиявляются
измеренными характеристиками случайной
величины, которые, вследствие их
определения только по части генеральной
совокупности, отличаются от фактических.
азванные
выше характеристики случайных процессов
являютсятеоретическими характеристиками,
описывающими все множество случайных
процессов (генеральную совокупность).
Их значения получить сложно и на практике
пользуются ихоценками, полученными
на основании экспериментальных выборок,
являющихся частью генеральных
совокупностей случайной величины.
Условно говоря,оценкиявляются
измеренными характеристиками случайной
величины, которые, вследствие их
определения только по части генеральной
совокупности, отличаются от фактических.
Математическое ожидание
![]() и его оценка – среднее
и его оценка – среднее
![]() характеризуют уровень, вокруг которого
колеблется случайная величина. Среднее
значение случайной величины определяется
по выражению
характеризуют уровень, вокруг которого
колеблется случайная величина. Среднее
значение случайной величины определяется
по выражению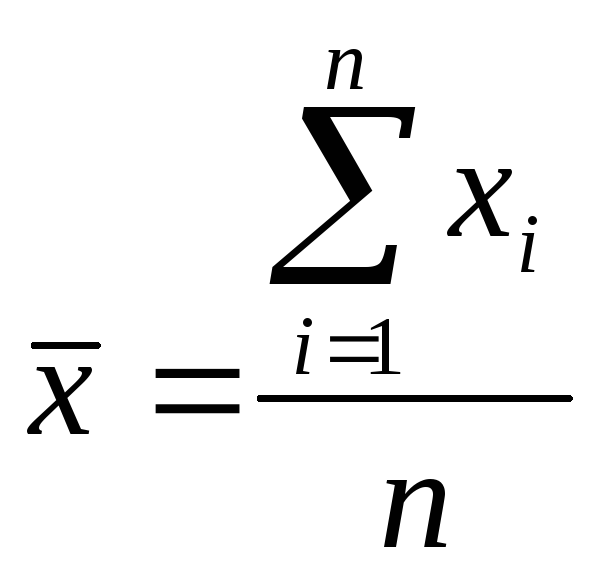 .
.
Здесь
![]() -
объем выборки (количество экспериментальных
данных). На рис. 1 приведены два случайных
процесса с различными средними значениями.
-
объем выборки (количество экспериментальных
данных). На рис. 1 приведены два случайных
процесса с различными средними значениями.
Д
 исперсия
исперсия![]() является
показателем ширины коридора колебания
случайной величины. Экспериментальнаяоценка дисперсии
является
показателем ширины коридора колебания
случайной величины. Экспериментальнаяоценка дисперсии
![]() определяется по выражению
определяется по выражению
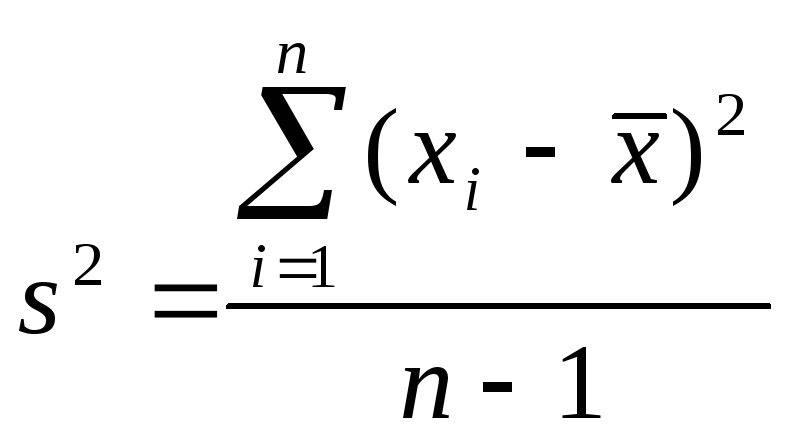 .
Корень квадратный из дисперсии
.
Корень квадратный из дисперсии![]() называетсясредним квадратическим
отклонением.Знание его оценки
называетсясредним квадратическим
отклонением.Знание его оценки![]() позволяет непосредственно определить
ширину коридора, в котором с заданной
вероятностью находится исследуемая
случайная величина. На рис. 2 приведены
два случайных процесса с одинаковыми
средними значениями и различными
дисперсиями.
позволяет непосредственно определить
ширину коридора, в котором с заданной
вероятностью находится исследуемая
случайная величина. На рис. 2 приведены
два случайных процесса с одинаковыми
средними значениями и различными
дисперсиями.
В отличие от детерминирован-ной
величины, описываемой функцией времени,
например,
![]() ,
значение случайной величины нельзя
точно предсказать. Но можно пред-сказать
вероятность нахождения случайной
величины в заданном коридоре. Ширина
коридора, в котором находится
,
значение случайной величины нельзя
точно предсказать. Но можно пред-сказать
вероятность нахождения случайной
величины в заданном коридоре. Ширина
коридора, в котором находится![]() значений случайной величины принимается
за весь коридор колебаний исследуемого
параметра.
значений случайной величины принимается
за весь коридор колебаний исследуемого
параметра.
Вероятность принятия случайной
величиной значения
![]() описыва-етсядифференциальной
функцией распределения
описыва-етсядифференциальной
функцией распределения
![]() Практически, вероятность показывает,
какая часть значений случайной величины
принимает данное значение (или находится
в заданном коридоре).
Практически, вероятность показывает,
какая часть значений случайной величины
принимает данное значение (или находится
в заданном коридоре).
При большом количестве влияющих факторов
случайная величина имеет нормальный
(гауссовый) закон распределения.
Дифференциальная функция нормального
закона распределения описывается
выражением
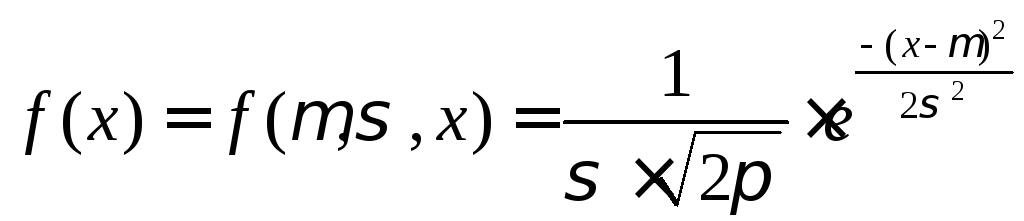
Для описания нормального закона
распределения надо знать две величины
(их оценки): математическое ожидание
![]() ,дисперсию
,дисперсию![]() .
На рис. 3 приведены дифференциальные
функции нормальных случайных процессов
с одинаковыми математическими ожиданиями
(
.
На рис. 3 приведены дифференциальные
функции нормальных случайных процессов
с одинаковыми математическими ожиданиями
(![]() )
и различными дисперсиями (
)
и различными дисперсиями (![]() ).
).
Дифференциальная функция нормального
закона распределения (и многих других)
теоретически не падает до нуля, т.к.
теоретически допускается возможность,
что случайная величина может принять
значения в диапазоне
![]() .
Например, температура воздуха в нашем
регионе может теоретически изменяться
от абсолютного нуля (при погасании
солнца) до миллионов градусов (при
превращении земли в звезду). При
исследованиях допустимый диапазон
изменения температуры ограничивают
практическими значениями и говорят,
что с вероятностью
.
Например, температура воздуха в нашем
регионе может теоретически изменяться
от абсолютного нуля (при погасании
солнца) до миллионов градусов (при
превращении земли в звезду). При
исследованиях допустимый диапазон
изменения температуры ограничивают
практическими значениями и говорят,
что с вероятностью![]() температура
находится в пределах, например:
температура
находится в пределах, например:![]() .
При увеличении ширины диапазона значение
доверительной вероятности увеличивается.
.
При увеличении ширины диапазона значение
доверительной вероятности увеличивается.
Т аким
образом, случайная величина характеризуется
двумя параметрами: шириной диапазона
и доверительной вероятностью - вероятностью
нахождения случайной величины внутри
данного диапазона. Поэтому при анализе
случайных процессов большое значение
имеют функции распределения.
аким
образом, случайная величина характеризуется
двумя параметрами: шириной диапазона
и доверительной вероятностью - вероятностью
нахождения случайной величины внутри
данного диапазона. Поэтому при анализе
случайных процессов большое значение
имеют функции распределения.
Ш
![]() находится 68% значений, соответственно,
в коридорах
находится 68% значений, соответственно,
в коридорах![]() и
и![]() находятся 95% и 99.6% значений случайной
величины (рис. 4).
находятся 95% и 99.6% значений случайной
величины (рис. 4).
Интегральная функция распределения
![]() показывает вероятность случайной
величины быть в коридоре
показывает вероятность случайной
величины быть в коридоре![]() .
Практически
.
Практически![]() показывает, какая часть случайной
величины меньше или равно значению
показывает, какая часть случайной
величины меньше или равно значению![]() ,
т.е.
,
т.е.![]() .
Значения
.
Значения![]() определяются:
определяются: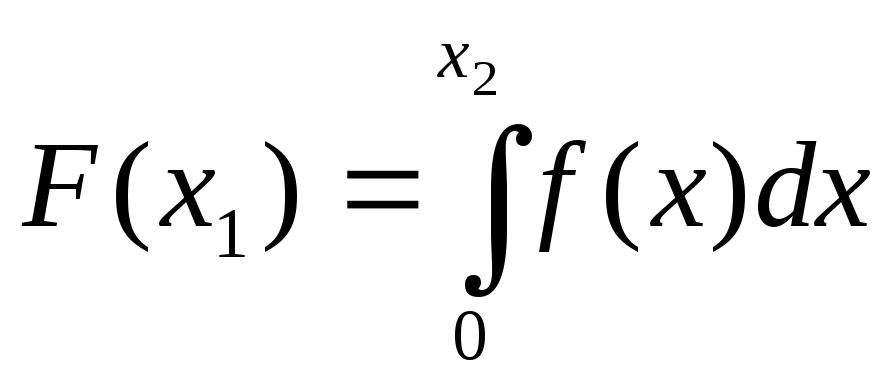 .
.
Вероятность нахождения в коридоре
![]() (какая часть значенийxнаходится в
данном коридоре) определяется по
выражению
(какая часть значенийxнаходится в
данном коридоре) определяется по
выражению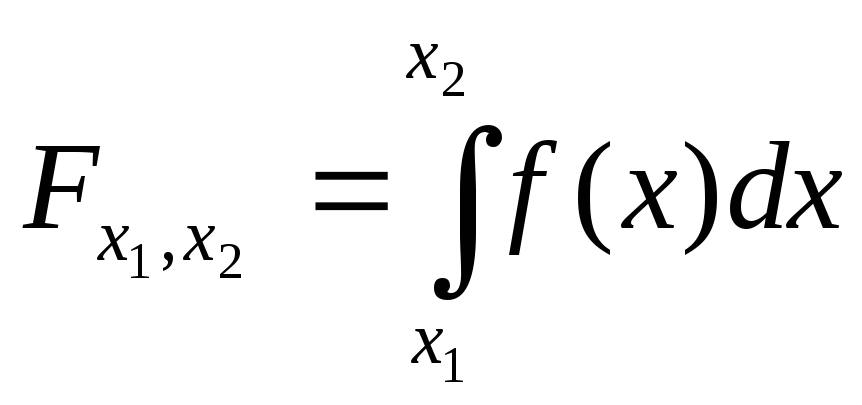 или
или![]() .
.
Вероятности нахождения случайных величин в заданных коридорах сведены в статистические таблицы. На компьютерах в различных пакетах для их вычисления имеются специальные операторы.
Н а
рис. 5 приведены графики трех случайных
процессовx1(t),x2(t),x3(t),
не отличающихся своими средними
значениями, дисперсиями и законами
распределения. Но они отличаются
скоростью изменения случайных величин
во времени или, говорят, они имеют
различные гармонические (спектральные)
составляющие. Эти свойства случайных
процессов надо учитывать при анализе
технологических процессов и систем
управления, т.к. сигналы с различными
частотами по-разному проходят через
технологические процессы и отрабатываются
элементами системы (согласно частотным
характеристикам).Для учета
этих свойств используются две
взаимосвязанные характеристики:
корреляционная функция
и спектральная
плотность.
а
рис. 5 приведены графики трех случайных
процессовx1(t),x2(t),x3(t),
не отличающихся своими средними
значениями, дисперсиями и законами
распределения. Но они отличаются
скоростью изменения случайных величин
во времени или, говорят, они имеют
различные гармонические (спектральные)
составляющие. Эти свойства случайных
процессов надо учитывать при анализе
технологических процессов и систем
управления, т.к. сигналы с различными
частотами по-разному проходят через
технологические процессы и отрабатываются
элементами системы (согласно частотным
характеристикам).Для учета
этих свойств используются две
взаимосвязанные характеристики:
корреляционная функция
и спектральная
плотность.
Корреляционная функция![]()
описывает степень связи между значениями
случайного процесса для сечений
случайного процесса, сдвинутых одно
относительно другого на величину . Эта связь изменяется в пределах от ±1
(+ прямая, - обратная функциональная
связь) до 0 (полное отсутствие связи) и
называется коэффициентом корреляции.
Зависимость коэффициента корреляции
от величины сдвига между этими сечениями
является корреляционной функцией.
Оценка корреляционной функции для
различных сдвигов![]() определяется
выражениями:
определяется
выражениями:
1. =0;![]()
2. =1;![]()
3 .=2;
.=2;![]()
Отметим, что
![]() является дисперсией случайного процесса
является дисперсией случайного процесса![]() .
.
Н а
рис. 6 приведены графики корреляционных
функцийRxx()
данных временных рядов. Первый временной
рядx1 во времени
изменяется быстро, для него корреляционная
связь между сечениями быстро убывает;
для второго эта связь убывает медленнее;
для третьего еще медленнее. Все это
проявляется во времени затухания
корреляционных функций. Чем медленнее
случайный процессx, тем больше
время затухания корреляционной функцииt3 >t2 >t1.
Следовательно, время затухания
корреляционной функции является
характеристикой скорости изменения
случайного процесса (характеризует
наличие спектральных составляющих).
а
рис. 6 приведены графики корреляционных
функцийRxx()
данных временных рядов. Первый временной
рядx1 во времени
изменяется быстро, для него корреляционная
связь между сечениями быстро убывает;
для второго эта связь убывает медленнее;
для третьего еще медленнее. Все это
проявляется во времени затухания
корреляционных функций. Чем медленнее
случайный процессx, тем больше
время затухания корреляционной функцииt3 >t2 >t1.
Следовательно, время затухания
корреляционной функции является
характеристикой скорости изменения
случайного процесса (характеризует
наличие спектральных составляющих).
Спектральная плотность– это прямое
преобразование Фурье от
корреляционной функции![]() .
.
Спектральная плотность имеет простой
физический смысл. Случайный сигнал
практически всегда можно представить
в виде суммы нескольких компонент (рис.
7):
![]() - среднее значение;
- среднее значение;
![]() - низкочастотная составляющая;
- низкочастотная составляющая;
![]() - среднечастотная составляющая;
- среднечастотная составляющая;
![]() - высокочастотная составляющая.
- высокочастотная составляющая.
Дисперсия х равна сумме дисперсий
компонент
![]()
 Построим следующий график (рис. 8). По
оси абсцисс отложим частоту составляющих,
а по оси ординат – их дисперсию. Мы
получили распределение дисперсии
процессахпо частотам. Это и есть
спектральная плотность. Площадь под
кривой спектральной плотностиS()равна дисперсии случайного процесса
Построим следующий график (рис. 8). По
оси абсцисс отложим частоту составляющих,
а по оси ординат – их дисперсию. Мы
получили распределение дисперсии
процессахпо частотам. Это и есть
спектральная плотность. Площадь под
кривой спектральной плотностиS()равна дисперсии случайного процесса![]() .
Дисперсия по определению - среднее
значение квадрата отклонения случайной
величины от среднего значения. Это
означает, что спектральная плотность
показывает распределение мощности
случайного процесса по частотам. Покажем,
что квадрат физической величины
отображает мощность этой величины на
примере простой электрической схемы.
Для этого рассмотрим мощность, выделяющуюся
в электрической цепи на сопротивленииR= 1Ом.
.
Дисперсия по определению - среднее
значение квадрата отклонения случайной
величины от среднего значения. Это
означает, что спектральная плотность
показывает распределение мощности
случайного процесса по частотам. Покажем,
что квадрат физической величины
отображает мощность этой величины на
примере простой электрической схемы.
Для этого рассмотрим мощность, выделяющуюся
в электрической цепи на сопротивленииR= 1Ом.
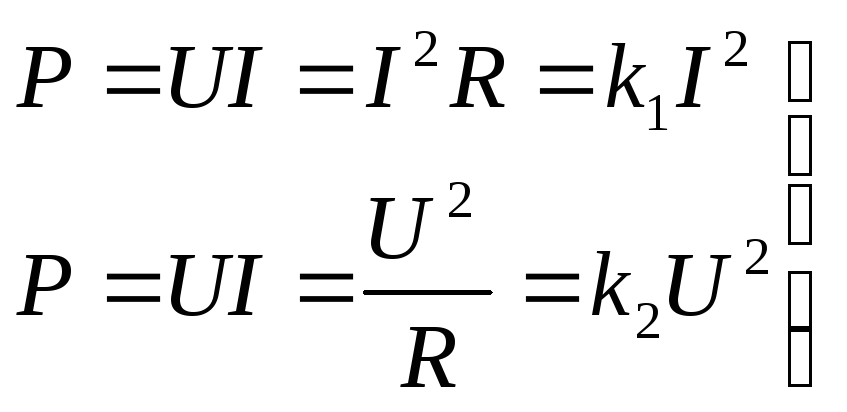
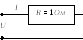

Таким образом, мощность электрического тока пропорциональна квадрату электрической величины тока или напряжения. Следовательно, дисперсия характеризует мощность переменной составляющей случайного процесса, а спектральная плотность S() показывает, какие частотные составляющие есть в сигнале и как мощность случайного процесса распределена по частотам.
Корреляционные функции и спектральные плотности имеют широкое применение, т.к. они позволяют проанализировать прохождение случайных сигналов через динамические звенья. Так при подаче на вход сигнала, равного автокорреляционной функции входного случайного процесса, на выходе будет сигнал, равный взаимокорреляционной функции входного и выходного случайных процессов. А спектральные плотности выходного и входного случайных процессов связаны квадратом модуля частотной характеристики динамического звена.
Введение в анализ систем управления. Дифференциальное уравнение - основная модель элементов и систем управления
Для исследования системы необходимо знать, как сигналы преобразуются элементами системы. Данные закономерности проявляются в процессе работы системы при подаче входных воздействий. Однако часто исследования реальной системы невозможно или экономически нецелесообразно. Поэтому анализ работы систем производят на математических моделях, которые описывают закономерности работы системы.
Анализ производится в следующей последовательности.
Задается модель сигналов (задающее, возмущающее воздействия).
Составляются уравнения для всех элементов системы.
Составляются уравнения для всей системы.
Исследуется устойчивость работы системы.
Исследуются качественные показатели работы системы при входных сигналах, соответствующих работе системы в реальных условиях.
При изучении закономерностей процессов часто не удается непосредственно найти законы, связывающие выходные переменные с входными, но возможно установить зависимости между переменными, их производными или дифференциалами. В результате математическое описание элементов системы осуществляется обычно в виде дифференциальных уравнений. Это связано также со свойством элементов системы накапливать и отдавать энергию в различных условиях работы. В общем виде линейное дифференциальное уравнениеn-го порядка с постоянными коэффициентами имеет вид:
![]()
Оно описывает связь между входным
![]() и выходным
и выходным![]() сигналами и их производными.
сигналами и их производными.
Р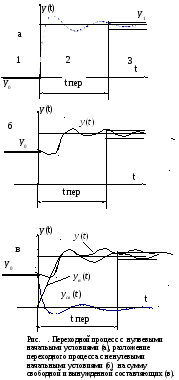 ешение
дифференциального уравнения ищется в
виде суммы свободной и вынужденной
составляющих
ешение
дифференциального уравнения ищется в
виде суммы свободной и вынужденной
составляющих![]() .
Свободная составляющая описывает
движение системы при отсутствии входного
сигнала (правая часть уравнения равна
нулю) и ненулевых начальных условиях,
например,
.
Свободная составляющая описывает
движение системы при отсутствии входного
сигнала (правая часть уравнения равна
нулю) и ненулевых начальных условиях,
например,![]() .
Вторая составляющая
.
Вторая составляющая![]() описывает движение системы при наличии
входного сигнала
описывает движение системы при наличии
входного сигнала![]() и нулевых начальных условиях. На рис.
а показано решение дифференциального
уравнения при ступенчатом изменении
входного сигнала и нулевых начальных
условиях. На рис. б показано изменение
выходного сигнала
и нулевых начальных условиях. На рис.
а показано решение дифференциального
уравнения при ступенчатом изменении
входного сигнала и нулевых начальных
условиях. На рис. б показано изменение
выходного сигнала![]() при
ступенчатом изменении входного сигнала
и начальном значении выходного сигнала
при
ступенчатом изменении входного сигнала
и начальном значении выходного сигнала![]() .
На рис. в данное изменение выходного
сигнала представлено в виде суммы
свободной составляющей, падающей отy0
до 0 и вынужденной составляющей
.
На рис. в данное изменение выходного
сигнала представлено в виде суммы
свободной составляющей, падающей отy0
до 0 и вынужденной составляющей![]() ,
изменяющейся от 0 до установившегося
значения.
,
изменяющейся от 0 до установившегося
значения.
Алгоритм решения дифференциального уравнения:
а) Отыскание общего решения однородного уравнения (свободной составляющей) при правой части уравнения, равной нулю.
б) Получение общего решения неоднородного уравнения.
в) Отыскание частного решения неоднородного уравнения вынужденной составляющей.
г) Получение частного решения уравнения.
Рассмотрим несколько примеров описания элементов систем дифференциальными уравнениями.
12. Математические модели простых
электрических RC-цепей.
Для получения требуемых динамических
характеристик систем управления часто
дополнительно к основным элементам
системы, обеспечивающим ее функционирование,
используются различные корректирующие
звенья. Простейшим их видом являются
электрические цепи на основе![]() сопротивлений,
емкостей и индуктивностей. Рассмотрим
модели простейших
сопротивлений,
емкостей и индуктивностей. Рассмотрим
модели простейших![]() -цепей.
-цепей.
К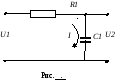 орректирующее
звено 1.Схема корректирующего звена
представлена на рис. Построим
математическую модель элемента в виде
дифференциального уравнения, описывающего
изменение напряжения на выходе
орректирующее
звено 1.Схема корректирующего звена
представлена на рис. Построим
математическую модель элемента в виде
дифференциального уравнения, описывающего
изменение напряжения на выходе![]() при изменении входного напряжения
при изменении входного напряжения![]()

Запишем уравнение 2-го закона Кирхгофа для замкнутого контура:
![]()
Значение тока в цепи выразим через
напряжение на конденсаторе
![]() .
.
Тогда
![]()
Перепишем выражение в стандартном виде – выходная переменная в левой части уравнения, входная – в правой, коэффициент при выходной переменной равен 1:
![]() ,
обозначим
,
обозначим![]()
![]()
Мы получили математическую модель, описывающую зависимость выходного напряжения от входного. Она имеет вид дифференциального уравнения первого порядка.
Корректирующее звено 2(схема на рис. ). Согласно 2-му уравнению Кирхгофа
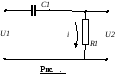
![]()
Продифференцируем уравнение:
![]()
Учитывая,
![]()
Запишем
![]()
Перепишем уравнение в типовой форме.
Получим дифференциальное уравнение,
описывающее зависимость тока от
напряжения входного сигнала
![]()
13. Математическая модель датчика
температуры. Пусть датчик температуры
из среды с температурой![]() поместили
в среду с температурой
поместили
в среду с температурой![]() .
Построим уравнение, описывающее изменение
температуры датчика. Составим уравнение
теплового баланса, компоненты которого
равны.
.
Построим уравнение, описывающее изменение
температуры датчика. Составим уравнение
теплового баланса, компоненты которого
равны.
Количество тепла, запасенного в датчике
массой mи теплоемкостьюc, равно:![]() .
Изменение
количества тепла в датчике за элементарное
времяdtравно:
.
Изменение
количества тепла в датчике за элементарное
времяdtравно:![]() .
.
Передача тепла от среды датчику за
время dtравно при поверхности
теплообменаFи коэффициенте
теплопередаче равно:![]() .
.
Уравнение теплового баланса
![]() или
или![]()
В стандартной форме уравнение будет
![]()
Обозначим
![]() ,
тогда математическая модель будет иметь
вид типового уравнения первого порядка
,
тогда математическая модель будет иметь
вид типового уравнения первого порядка![]()
1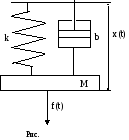 4.
Математическая модель механической
колебательной системы.На механическую
систему, содержащую пружину жесткостьюk, демпфер с коэффициентом
вязкостиb, тело массойM(рис. ) действует силаf(t).
Необходимо построить математическую
модель, описывающую движение системыx(t) во
времени. Составим уравнение движения
на основе второго закона Ньютона.
4.
Математическая модель механической
колебательной системы.На механическую
систему, содержащую пружину жесткостьюk, демпфер с коэффициентом
вязкостиb, тело массойM(рис. ) действует силаf(t).
Необходимо построить математическую
модель, описывающую движение системыx(t) во
времени. Составим уравнение движения
на основе второго закона Ньютона.
Момент инерции системы равен:
![]() .
.
Сила упругости пружины:
![]()
Сила сопротивления движению демпфера:
![]() .
.
Уравнение равновесия сил Ньютона
![]()
![]()
Мы получили дифференциальное уравнение второго порядка.
1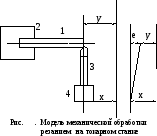 5.
Математическая модель упругого узла
подачи резца.На рис. приведена
схема обработки вала 1 на токарном станке
резцом 3. Построим математическую модель
жесткости механической системы резец
– резцедержатель при продольной подаче.
Систему патрон-деталь считаем абсолютно
жесткой. При подаче резцедержателя на
величинуxрежущая кромка
подается на величинуy.
Ошибка подачи режущей кромки, вследствие
деформации резца (схема в правой части
рисунка), равна
5.
Математическая модель упругого узла
подачи резца.На рис. приведена
схема обработки вала 1 на токарном станке
резцом 3. Построим математическую модель
жесткости механической системы резец
– резцедержатель при продольной подаче.
Систему патрон-деталь считаем абсолютно
жесткой. При подаче резцедержателя на
величинуxрежущая кромка
подается на величинуy.
Ошибка подачи режущей кромки, вследствие
деформации резца (схема в правой части
рисунка), равна
![]()
Сила резания равна продольной силе,
приложенной к резцу, которую при жесткости
системы резцедержатель-резец kможно определить по выражению:![]()
Сила резания пропорциональна скорости
резания
![]() .
.
Момент инерции при массе подвижной
части mравен![]() .
.
Уравнение движения на основании второго
закона Ньютона
![]()
Дифференциальное уравнение механической системы имеет вид
![]()
Методы решения дифференциальных уравнений:
Кратко напомним следующие методы решения дифференциальных уравнений.
Классический метод.
Метод Коши.
Метод преобразования Лапласа.
Численный метод.
Классический метод решения дифференциальных уравнений
Решение линейного однородного
дифференциального уравненияс
постоянными коэффициентами.![]()
Т.к. входной сигнал равен 0 (правая часть
уравнения равно 0), то решение имеет
смысл при ненулевых начальных условиях
![]()
Решение описывает переход системы из начального ненулевого состояния в нулевое состояние. Решение зависит от вида корней характеристического уравнения
![]()
Возможны следующие четыре случая.
1. Все корни характеристического уравнения действительные и различные (нет кратных корней). Решение записывается в виде
![]()
2. Все корни вещественные, но имеется корень кратности k
![]()
3. Имеется одна пара комплексных
сопряженных корней
![]()
![]()
4. Имеются кратные комплексные корни
![]()
![]() Примеры.
Решить уравнение 1.
Примеры.
Решить уравнение 1.![]()
Запишем характеристическое уравнение
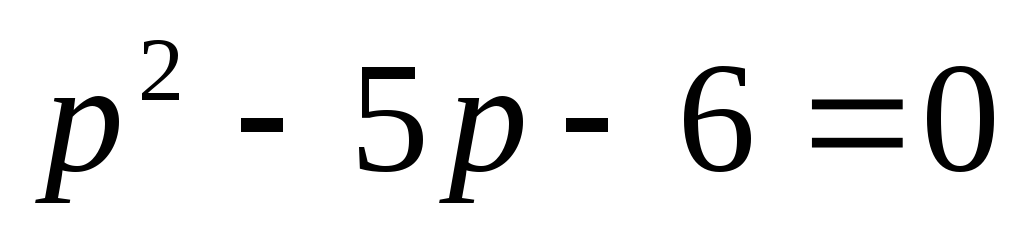 .
.Найдем корни уравнения
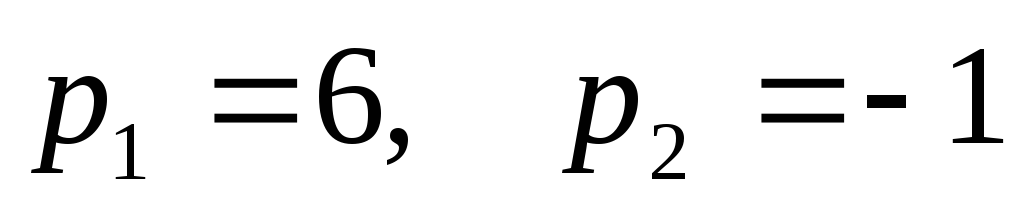
Запишем свободную составляющую решения дифференциального уравнения
![]()
Решить уравнение 2.
![]()
Запишем характеристическое уравнение
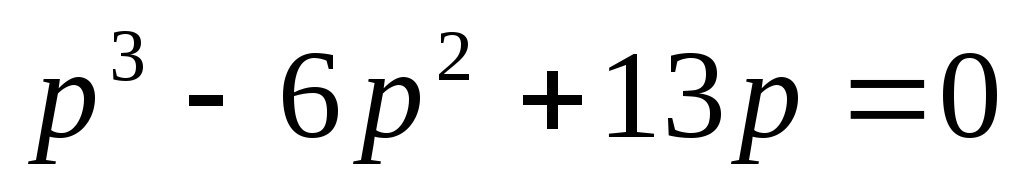 .
.Найдем корни уравнения
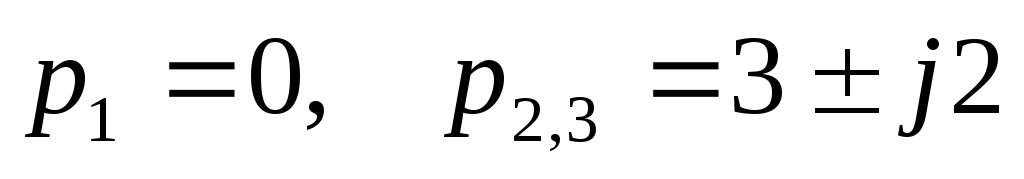
Запишем свободную составляющую решения дифференциального уравнения
![]()
Решить уравнение 3.
![]() при начальных условиях
при начальных условиях![]()
Запишем характеристическое уравнение
 .
.Найдем корни уравнения
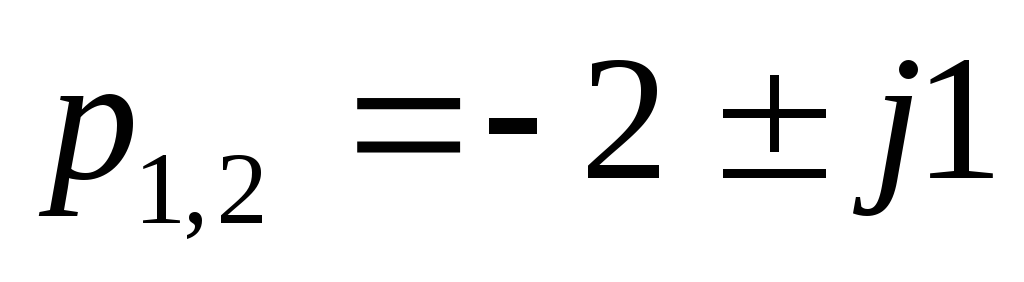
Запишем свободную составляющую решения дифференциального уравнения
![]()
Для нахождения значений
 используем начальные условия.
используем начальные условия.
1НУ. При
![]()
![]()
2НУ. Найдем 1-ю производную от решения
![]()
![]()
![]()
При
![]()
![]()
![]()
Полученное частное решение
![]()
Это решение единственное, оно определяется начальными условиями нахождения выходной переменной, поэтому решение называется частным.
Решение линейного неоднородного дифференциального уравненияс постоянными коэффициентами. Для нахождения полного решения неоднородного дифференциального уравнения к найденным выше свободным составляющим, являющихся решениями однородных уравнений необходимо найти вынужденные составляющие, определяемые видом правой части неоднородного уравнения. Для некоторых видов законов изменения входной переменной частное решение можно указать по виду правой части дифференциального уравнения. В более общих случаях решение ищется методом квадратур [].
1 случай. Правая часть имеет вид
![]()
где:
![]() - многочлен, описывающий изменение
входной переменной во времени.
- многочлен, описывающий изменение
входной переменной во времени.
Данный случай описывает сигналы:
Постоянный входной сигнал
![]() приk=0, P(t)=x0
приk=0, P(t)=x0
Линейно изменяющийся входной сигнал
![]() и др.
и др.
В данном случае
![]() есть функция, подобная исходной, но со
своими коэффициентами.
есть функция, подобная исходной, но со
своими коэффициентами.
2 случай. Правая часть имеет вид
![]()
3 случай. Правая часть является суммой
![]()
Для случаев 2, 3 выходной сигнал также есть функция, подобная виду входного сигнала.
4 случай. Если kдля
случая 1 или![]() для случая 2 являются корнями
характеристического уравнения системы,
то к данному решению добавляется
множитель
для случая 2 являются корнями
характеристического уравнения системы,
то к данному решению добавляется
множитель![]()
![]()
Рассмотрим пример1. Найти решение
дифференциального уравнения
![]()
Запишем характеристическое уравнение
 .
.Найдем корни уравнения
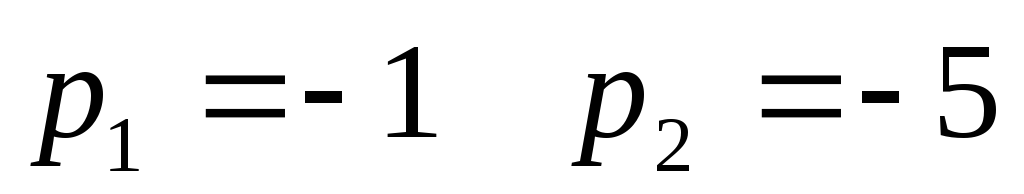
Запишем свободную составляющую решения дифференциального уравнения
![]()
Находим вынужденное решение. Входной сигнал относится к случаю 1.
![]() - полином 2-й степени.k=0и не является корнем характеристического
уравнения.
- полином 2-й степени.k=0и не является корнем характеристического
уравнения.
Ищем решение в виде полинома 2-й степени
![]()
Находим
![]() подставляем их в исходное уравнение
подставляем их в исходное уравнение
![]()
![]()
Приравнивая коэффициенты при одинаковых степенях t
![]()
![]()
![]()
Вынужденная составляющая
![]()
Общее решение
![]()
Рассмотрим пример 2.
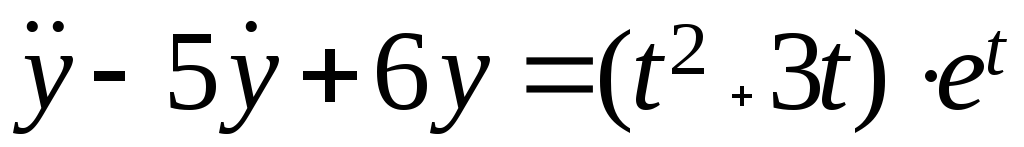
![]() при
нулевых начальных условиях.
при
нулевых начальных условиях.


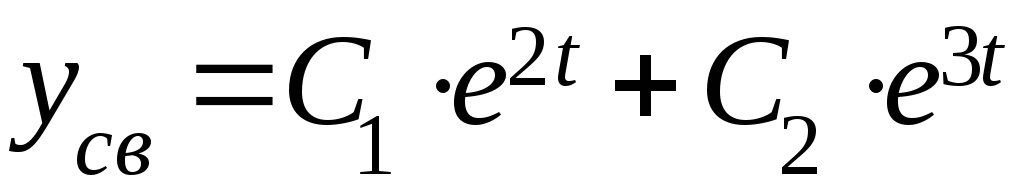
L(t) e kt, k=1pi.
y(t)=M(t)ekt = (At2+Bt+C)et
![]()
![]()
=![]()
Преобразуем и приравняем к правой части нашего исходного уравнения.
![]()
![]() A=1/2, B=3, C=4.
A=1/2, B=3, C=4.
![]()
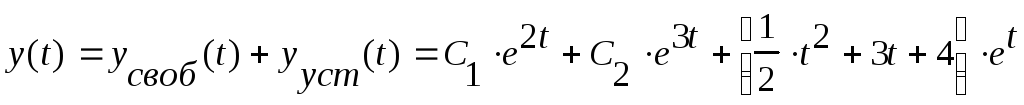
Собственные решения (t=0).
![]()
![]()
![]() С1=1, С2=-5.
С1=1, С2=-5.
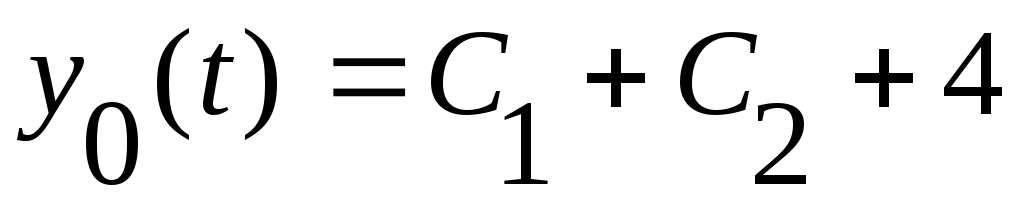
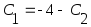
![]() С1=1, С2=-5.
С1=1, С2=-5.
Решение дифференциального уравнения 1-го порядка классическим методом
Решение
дифференциального уравнения заключается
в нахождении зависимости изменения во
времени выходной переменной
![]() при следующих исходных данных:
при следующих исходных данных:
дифференциальное уравнение с параметрами k,Т;
начальное значение выходной переменной
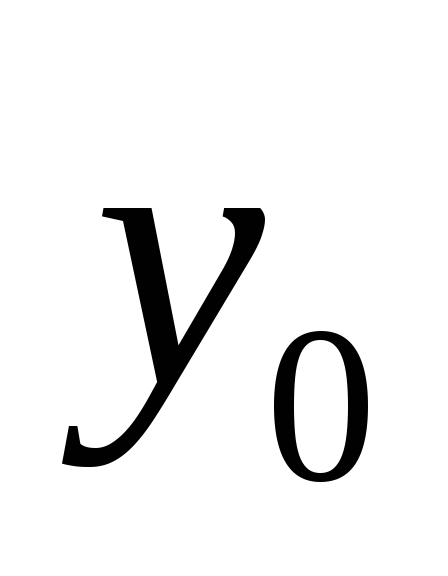 ;
;закон изменения во времени входной переменной
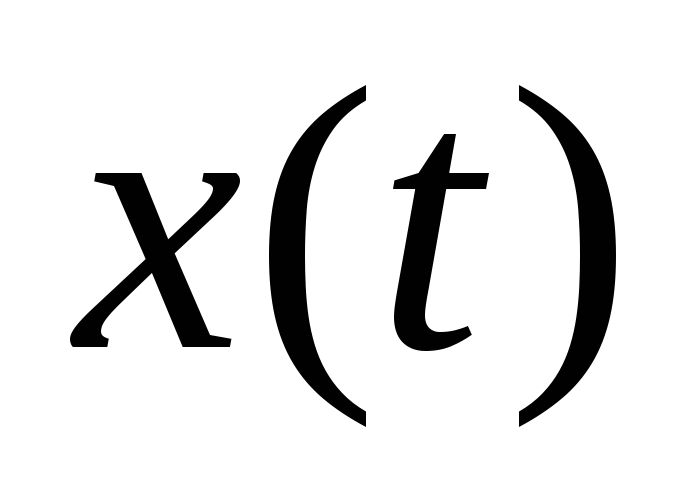 .
.
Найдем решение дифференциального
уравнения
![]() при постоянном значении входного сигнала
при постоянном значении входного сигнала![]() .
.
Решение ищем в виде суммы свободной и вынужденной составляющих
![]()
Находим свободную составляющую решения:
- запишем характеристическое уравнение
![]() ;
;
- найдем корень уравнения
![]() ;
;
- запишем свободную составляющую решения дифференциального уравнения:
![]() .
.
Находим вынужденное решение. Входной сигнал
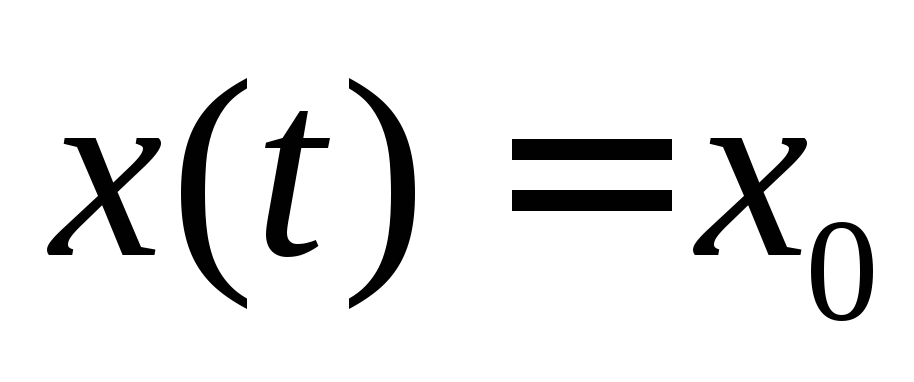 относится к полиномам. Поэтому ищем
решение в виде такого же полинома
относится к полиномам. Поэтому ищем
решение в виде такого же полинома
![]() .
.
Для нахождения значения В подставляем решение в исходное уравнение
![]() ,
,![]() ,
тогда
,
тогда![]() .
.
Вынужденная составляющая
![]() .
.
Общее решение
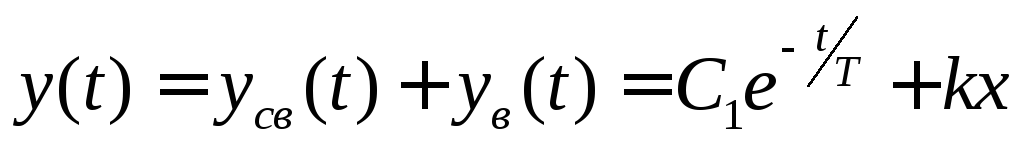
Используя начальные условия, найдем постоянную
 :
:
при
![]()
![]() ,
отсюда
,
отсюда![]()
Решение уравнения при постоянном входном сигнале
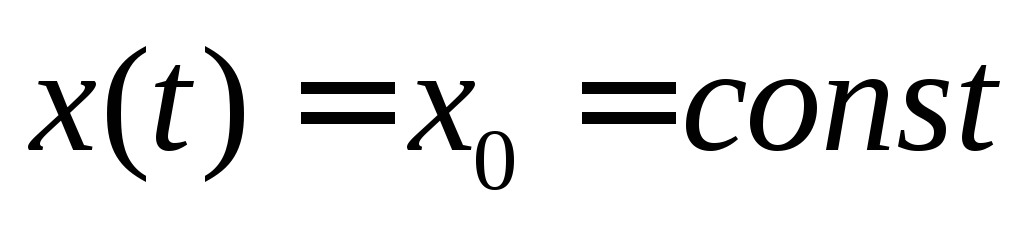
![]() .
.
Первый элемент выражения отражает
влияние начальных условий и показывает,
что начальное значение
![]() уменьшается по экспоненциальному
закону с постоянной времени Т.
уменьшается по экспоненциальному
закону с постоянной времени Т.
Второй элемент выражения отражает
влияние входного сигнала при нулевых
начальных условиях и показывает, что
при подаче на вход звена первого порядка
постоянного сигнала выходной сигнал
по экспоненциальному закону с постоянной
времени Т выходит на значение
![]() .
.
Время падения первого элемента и выхода
второго элемента на расчетное значение
с точностью 5% (вход в 5% трубку от расчетного
значения) называется временем переходного
процесса и составляет
![]() .
.
