3) Обратное преобразование Лапласа.

1.Для упрощения разложим полученное уравнение на простые дроби.

K₃=18

2.Обратное преобразование Лапласа (метод вычетов).рннр

В теории комплексного переменного имеется теорема о вычетах, которая используется для получения обратного преобразования Лапласа.

,

, гдеn- количество корней.

Выражение для определения вычетов зависит от вида характеристического полинома x(p)илиM(p)=0.

1) Простые корни, не равные друг другу (p    j , p₁  p₂).

, гдеq- количество простых корней.

2) Пусть характеристическое уравнение M(p)=0имеет кратные корни (например,p_r- корни кратностиr;p_s- корни кратностиs).

Пример:Пусть после решения уравнения в операторном виде мы получили:

,

N(p)=1,

M(p)=0,  p₁=p₂=0, p₃=-

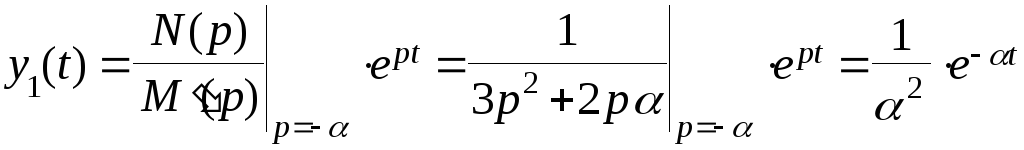
Взаимосвязь моделей и характеристик динамических звеньев

Получаемая характеристика	Исходная характеристика

107