2.7.4. Колебательное звено

Его уравнение: T₁²p²y + T₂py + y = ku.

Передаточная функция:

Решение уравнения зависит от соотношения постоянных времени T₁ и T₂, которое определяет коэффициент затухания (демпфирования) . Можно записать

, где T = T₁.

Если ξ ≥ 1, то знаменатель W(p) имеет два вещественных корня p₁ и p₂ и раскладывается на два сомножителя:

T₂p² + 2ξTp + 1 = T₂(p - p₁).(p - p₂).

Такое звено можно разложить на два апериодических звена первого порядка, поэтому оно не является элементарным.

Рис.2.23

При ξ <1 корни полинома знаменателя W(p) комплексно сопряженные: p_1,2 = α± jω. Переходная характеристика представляет собой выражение, характеризующее затухающий колебательный процесс с декрементом затухания и частотойω (рис.2.23). Такое звено называется колебательным. При ξ= 0 колебания носят незатухающий характер. Такое звено является частным случаем колебательного звена и называется консервативным. Примерами колебательного звена являются пружина, имеющая успокоительное устройство, электрический колебательный контур с активным сопротивлением и т.п. Зная характеристики реального устройства можно определить его параметры как колебательного звена. Так передаточный коэффициент k равен установившемуся значению переходной функции.

При k = 1 передаточная функция звена:

В виду сложности вывода выражений для частотных характеристик рассмотрим их без доказательства, они показаны на рис.2.24.

Рис.2.24 Рис.2.25

Асимптотическая ЛАЧХ колебательного звена до сопрягающей частоты ω₁ = 1/T₁ совпадает с осью абсцисс, при дальнейшем увеличении частоты идет с наклоном - 40 дб/дек. То есть, высокие частоты колебательное звено «заваливает» сильнее, чем апериодическое звено.

В предельном случае ξ= 0 получаем консервативное звено, у которого при ω≈ ω₁ амплитуда выходных колебаний стремится к бесконечности (рис.2.25).

ЛФЧХ при малых частотах асимтотически стремится к нулю. При увеличении частоты до бесконечности выходной сигнал поворачивается по фазе относительно входного на угол, стремящийся в пределе к - 180^º. При уменьшении коэффициента демпфирования АФЧХ приближается к оси абсцисс и в пределе у консервативного звена она вырождается в два луча по оси абсцисс, при этом фаза выходных колебаний скачком меняется от 0^º до - 180^º при переходе через сопрягающую частоту (рис.2.25).

2.7.5. Дифференцирующее звено

Различают идеальное и реальное дифференцирующие звенья. Уравнение динамики идеального звена: , или y = kpu. Здесь выходная величина пропорциональна скорости изменения входной величины.

Передаточная функция: W(p) = kp.

При k = 1 звено осуществляет чистое дифференцирование W(p) = p.

Переходная характеристика: h(t) = k1^'(t) = δ(t).

Идеальное дифференцирующее звено реализовать невозможно, так как величина всплеска выходной величины при подаче на вход единичного ступенчатого воздействия всегда ограничена. На практике используют реальные дифференцирующие звенья, осуществляющие приближенное дифференцирование входного сигнала.

Его уравнение: Tpy + y = kTpu.

Передаточная функция:

При малых Т звено можно рассматривать как идеальное дифференцирующее. Переходную характеристики можно вывести с помощью формулы Хевисайда:

,

здесь p₁ = - 1/T - корень характеристического уравнения D(p) = Tp + 1 = 0; кроме того, D^'(p₁) = T.

При подаче на вход единичного ступенчатого воздействия выходная величина оказывается ограничена по величине и растянута во времени (рис.2.26). По переходной характеристике, имеющей вид экспоненты, можно определить передаточный коэффициент k и постоянную времени Т. Примерами таких звеньев могут являться четырехполюсник из сопротивления и емкости или сопротивления и индуктивности, демпфер и т.п. Дифференцирующие звенья являются главным средством, применяемым для улучшения динамических свойств САУ.

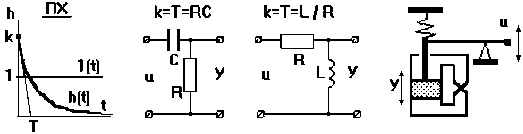
Рис.2.26

Для идеального дифференциатора частотные характеристики определятся соотношениями:

АФЧХ: ;

ВЧХ: P(ω) = 0;

МЧХ: Q(ω) = jkω;

АЧХ: А(ω) = kω;

ФЧХ: φ(ω) = π/2;

ЛАЧХ: L(ω) = 20lgk+20lgω.

Частотные характеристики дифференциатора представлены на рис.2.27.