Лекция 1 План лекции

1. Понятие комплексного числа.

2. Комплексная плоскость. Тригонометрическая форма записи комплексных чисел.

3. Извлечение корня из комплексного числа.

4. Понятие области на комплексной плоскости.

ЭЛЕМЕНТЫ ТЕОРИИ ФУНКЦИЙ КОМПЛЕКСНОГО ПЕРЕМЕННОГО.

1. Комплексная плоскость. Тригонометрическая форма записи комплексного числа.

Комплексным числом называется выражение вида , гдеидействительные числа,- мнимая единица (), причеми т.д.

Р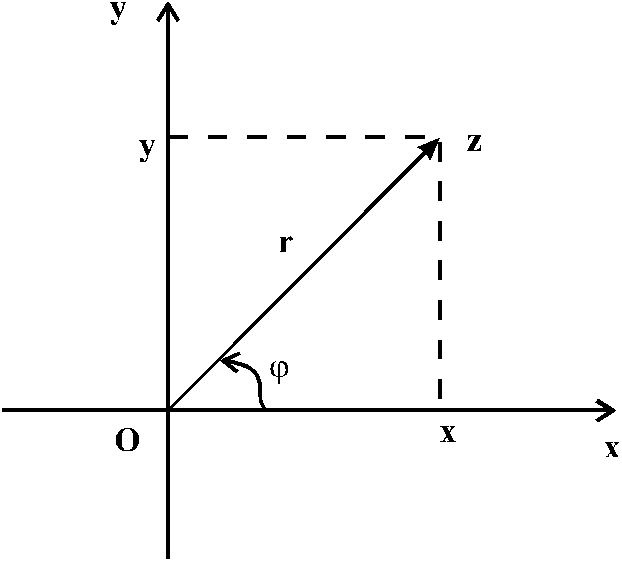ассмотрим плоскость с прямоугольной декартовой системой координат. Такая плоскость называется комплексной. Точку на комплексной плоскости можно задать с помощью радиусаи полярного угла.

- модуль комплексного числа ,;- аргумент числа.

За положительное направление угла принят отсчет против часовой стрелки от положительного направления оси.

Аргумент комплексного числа является неоднозначной величиной и задается с точностью до слагаемого кратного двум. В дальнейшем аргумент, как многозначную величину будем обозначать , а для конкретности сохраним.

Главное значение аргумента: .

Из рисунка видно, что

;

таким образом

- тригонометрическая форма записи комплексного числа.

;

; ;;

;

;

- формула Муавра.

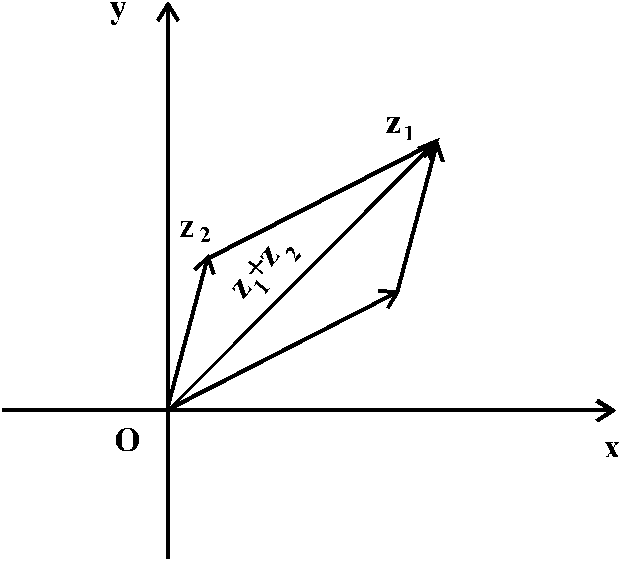
Точки на комплексной плоскости, а, следовательно, и комплексные числа можно задать с помощью вектора. При сложении и вычитании комплексных чисел используют общие правила сложения и вычитания векторов.

Извлечение корня из комплексного числа.

(*)

Пусть - корни. Из равенства (*) следует, что

(**)

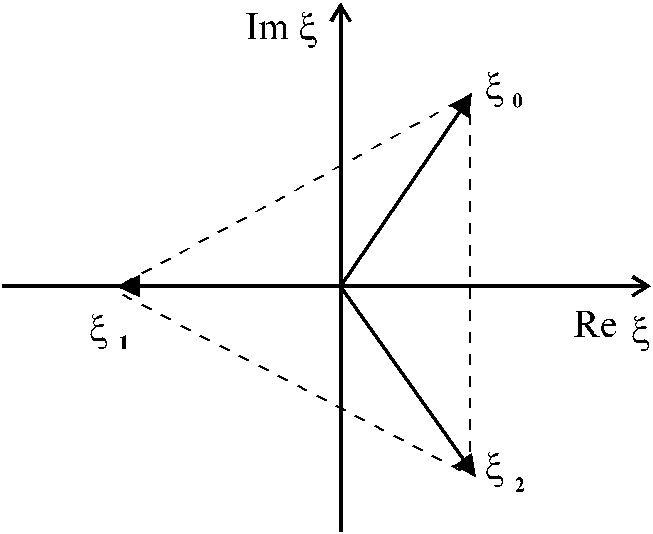
Из равенства (**) следует, что если комплексные корни изобразить на комплексной плоскости в виде вектора, то вершины этих векторов будут лежать в углах правильного -угольника, вписанного в окружность радиуса.

Пример.Найдем корень третьей степени из числа –1.

; ;

;

;

, ;

,

, .

Функции комплексного переменного.

1.Область на комплексной плоскости.

Областью на комплексной плоскости называется множество D точек z, удовлетворяющих следующим свойствам:

1) вместе с каждой точкой z из множества D области принадлежит и некоторый круг с центром в данной точке: (свойство открытости);

2) любые две точки можно соединить линией, состоящей из точек множества (свойство связанности).

Рис. 1

Простейшим примером области является понятие  окрестности на комплексной плоскости.

Под  окрестностью точки а понимают открытый круг радиуса с центром в точке а (рис. 2), т.е. множество точек z удовлетворяют неравенству:.

Рис.2

Точка z называется граничной точкой области, если сама она области не принадлежит, но любая ее  окрестность содержит точки из области D. Совокупность граничных точек образует границу области D.

Мы будем рассматривать те области, границы которых состоят из конечного числа линий и разрезов: например на рис.3 представлена односвязная область, а на рис.4 трехсвязная область.

Рис. 3

Рис. 4

Число связанных частей, на которое разбивается граница области D называется порядком связанности области.

Область, присоединяющая границы, называется замкнутой областью и обозначается .