Лекция 17

План лекции

1. Связь между обычным преобразованием Лапласа и D и Z- преобразованиями. Преобразование.

2. Основные теоремы Z - преобразования.

3. Краткий обзор содержания курса.

Связь между обычным преобразованием лапласа и d и z- преобразованиями. Преобразование.

Пусть преобразование Лапласа , а дискретное преобразование Лапласа. Между преобразованием Лапласа и Д – преобразованием имеет место соотношение

(1)

Для смещенных решетчатых функций

(2)

Равенства (1) и (2) позволяют установить связь между обычным преобразованием Лапласа и Z – преобразованием. Для этого достаточно положить . Равенства (1) и (2) при этом принимают вид

(3)

(4)

Существует более простая связь между обычным преобразованием Лапласа и Д – и Z – преобразованиями.

(5)

В равенстве (5) вычеты берутся по всем особым точкам функции F(s).

Для смещенных решетчатых функций

(6)

В равенстве (6) вычеты берутся по всем особым точкам функции F(s).

Для того чтобы от (5) и (6) перейти к соотношениям, связывающим обычное преобразование Лапласа с Z – преобразованием, достаточно положить .

(7)

(8)

В равенствах (7) и (8) вычеты берутся по всем особым точкам функции F(s).

Свойства z – преобразования.

1. Линейность преобразования.

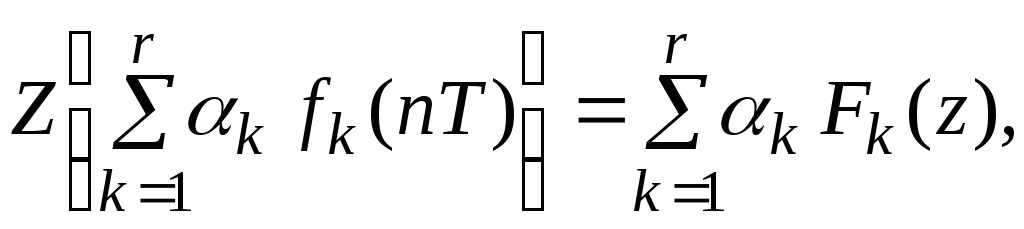
некоторые числа.

2. Z – преобразование смещенной функции.

Теорема 2.

Если решетчатая функция f(nT) является оригиналом и Z – преобразование этой функции F(z), то

а) Z – преобразование функции Z[f(n+m)]

б)

Доказательство.

По определению

Положим n + m = r, тогда

.

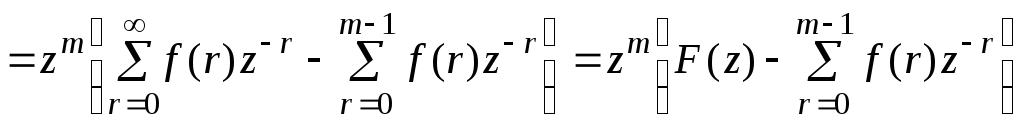Пункт б доказывается аналогично, причем при

3. Смещение в области изображений.

Теорема 3.

Если функция f(nT) является оригиналом и Z – преобразование этой функции F(z), то

.

Доказательство.

По определению

.

4. Z – изображение конечной разности.

Теорема 4.

Если функция f(nT) является оригиналом и Z – преобразование этой функции F(z), то

Доказательство.

По определению

В соответствии с теоремами 1 и 2

5. Преобразование конечной суммы.

Теорема 5.

Если функция f(n) является оригиналом и Z – преобразование этой функции F(z), то

.

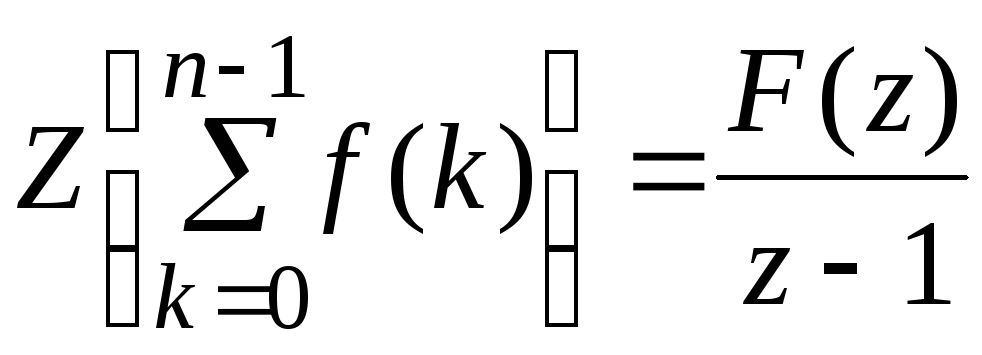Выше было показано, что конечная разность

, (*)

т. е. конечная сумма является первообразной функции f(n).

Применим к равенству (*) Z – преобразование

(**)

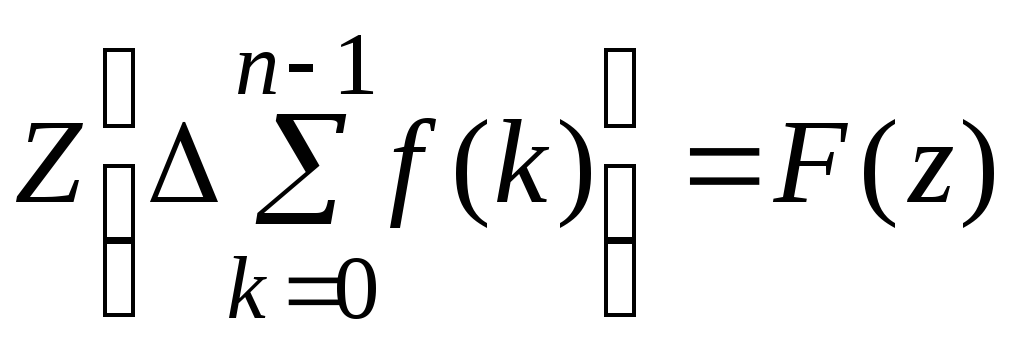по теореме 4

(***)

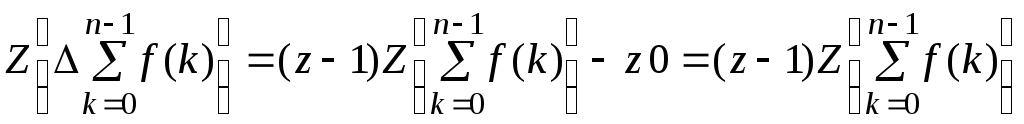Принимая во внимание равенство (**), из (***) получим

.

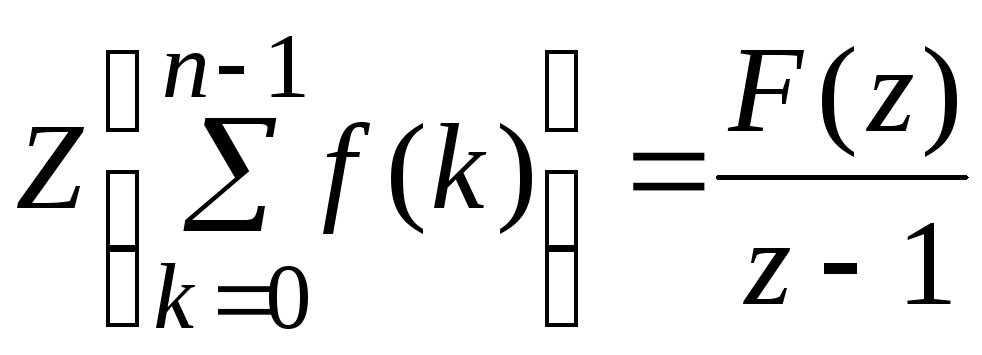6. Начальное значение решетчатой функции.

Теорема 6.

Если функция f(n) является оригиналом и Z – преобразование этой функции F(z), то

Доказательство.

По определению

Перейдя к пределу, получим

7. Предельное значение решетчатой функции.

Теорема 7.

Если функция f(n) является оригиналом и Z – преобразование этой функции F(z) и если (z - 1)F(z) – аналитическая функция в области , то

Доказательство.

Рассмотрим сумму

(*)

по теореме 4

или

Перейдем к пределу при (предел существует, т. к. по условию теоремы функция (z - 1)F(z) – аналитическая функция в области ).

Принимая во внимание (*), найдем

8. Преобразование свертки функции.

Сверткой функции иназывается функция , равная

.

Имеет место коммутативность

.

Теорема 8.

Если функции иявляются оригиналами иZ – преобразование этих функций, соответственно, F₁(z) и F₂(z), то